
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрические колебания и электромагнитные волны.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОВЕРКИ УСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА 1. Что может служить источником переменного электромагнитного поля (электромагнитного излучения)? 2. Какова взаимная ориентация в электромагнитной волне векторов напряжённостей электрического и магнитного полей и электромагнитного луча? 3. Частота колебаний электрического заряда равна n. Какова частота излучаемых при этом электромагнитных волн? 4. Как называют электромагнитные волны частотой порядка 1015 Гц? 5. Электрический заряд колеблется в горизонтальной плоскости. В какой плоскости находится электрическая составляющая электромагнитной волны, создаваемой этим колебанием? 6. Какие значения имеют напряжённость Е электрического поля конденсатора и напряжённость Н магнитного поля катушки самоиндукции колебательного контура, когда сила тока в нём максимальна? 7. Опишите (подробно) процесс электрических колебаний в колебательном контуре (для одного периода колебания). 8. Почему электрические колебания в колебательном контуре затухают? 9. Как изменится период электрических колебаний в колебательном контуре, если ёмкость его конденсатора уменьшится в четыре раза? 10. Нарисуйте схему автоколебательного контура с электронной лампой и объясните принцип его действия. 11. Как часто в автоколебательном контуре с электронной лампой совершается «подзарядка» конденсатора? 12. Период электрических колебаний в колебательном контуре уменьшился в три раза. Как изменилась мощность электрического излучения контура? 13. Что называется звуковым модулированием электрических колебаний? 14. Нарисуйте принципиальные схемы радиопередатчика и радиоприёмника и объясните процесс телефонной радиосвязи (от поступления звука в микрофон до его воспроизведения телефоном). 15. Чем заменяют микрофон передатчика и телефон приёмника в системе телефонной радиосвязи при её использовании для телевизионной радиосвязи? 16. Почему непосредственная радиосвязь возможна только на малых расстояниях (прямой видимости между антеннами передатчика и приёмника)? 17. На экране электронно-лучевой трубки радиолокатора расстояние между пиками отправленного и отражённого от объекта электромагнитных импульсов d = 10 мм. Скорость движения по экрану электронного луча, производящего горизонтальную развёртку, u = 1 м/с. Чему равно расстояние от локатора до объекта?
ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
Примеры решения задач
Пример 1. По двум длинным прямолинейным и параллельным проводам, расстояние между которыми d = 4 см, в противоположных направлениях текут токи I 1 = 0,3 A, I 2 = 0,5 A. Найти магнитную индукцию в точке А, которая находится на расстоянии r 1 = 2 см от первого провода на продолжении линии, соединяющей провода (рис. 1).
Для того чтобы найти направление векторов
полей, созданных точками I 1 и I 2. Силовые линии магнитного поля прямого провода с током представляют собой концентрический окружности с центром на оси провода. Направление силовой линии совпадает с движением концов рукоятки правого буравчика, ввинчиваемого по направлению тока (правило буравчика). Поэтому силовая линия магнитного поля тока I 1, проходящая через точку А, представляет собой окружность радиусом I 1 A, а силовая линия магнитного поля тока I 2, проходящая через эту же точку, – окружность радиусом I 2 A (на рис. 6 показана только часть этой окружности). По правилу буравчика находим, что силовая линия магнитного поля тока I 1 направлена против часовой стрелки, а тока I 2 – по часовой стрелке. Теперь легко найти направление векторов В = В 1 – В 2. (2) Индукция магнитного поля тока I, текущего по прямому бесконечному длинному проводу, вычисляется по формуле В = где m0 – магнитная постоянная; m – магнитная проницаемость среды в которой провод расположен; r – расстояние от провода до точки, в которой определяется индукция. Подставив значения В 1 и В 2 в равенство (2), получим В = или В = Выразим числовые значения в СИ и подставим их в (4): m0 = 4p·10–7 Н/А2 = 4p·10–7 Гн/м; m = 1 (провода расположены в воздухе); I 1 = 0,3 А; I 2 = 0,5 A; r 1 = 0,02 м; r 2 = 0,06 м; В =
Пример 2. Из проволоки диаметром d = 0,1 мм и сопротивлением R = 25 Ом намотан соленоид на картонном цилиндре (витки прилегают друг к другу). Определить индукцию магнитного поля на оси соленоида, если напряжение на концах обмотки U = 2 В. Р е ш е н и е. Индукция магнитного поля на оси соленоида вычисляется по формуле В = m0m I n, (1) где п – число витков на единицу длины соленоида; I – сила тока, текущего по обмотке соленоида. Число витков п получим, разделив единицу длины на диаметр проволоки п = Силу тока, текущего по обмотке, найдём по закону Ома для участка цепи I = Подставим значения п и I в равенство (1) В = m0m Выпишем числовые значения величин в СИ и подставим их в расчётную формулу (2): m0 = 4p·10–7 Гн/м; m = 1; d = 0,1 мм = 10–4 м; U = 2 B; R = 25 Ом; В = 4p·10–7 · 1
Пример 3. Прямой провод длиной l = 10 см, по которому течёт ток I = 0,5 A, помещён в однородное магнитное поле перпендикулярно силовым линиям. Найти индукцию магнитного поля, если оно действует на прямой провод с силой F = 2,6 мН. Р е ш е н и е. Сила F, с которой однородное магнитное поле действует на прямой провод с током, вычисляется по формуле закона Ампера F = IBl sin a, (1) где I – сила тока, текущего по проводнику; l – длина проводника; В – индукция магнитного поля, в которое проводник помещён; a – угол между направлением тока и направлением линий индукции. Из формулы (1) найдём В = Выпишем числовые значения единиц в СИ и подставим их в расчётную формулу (2): F = 2,6 мН = 2,6·10–3 Н; I = 0,5 A; l = 10 см = 0,1 м; a = 90°; sin a = 1; В =
Пример 4. Протон, пройдя ускоряющую разность потенциалов U = 400 B, влетел в однородное магнитное поле с индукцией В = 0,2 Тл и начал двигаться по окружности. Вычислить радиус окружности. Р е ш е н и е. На заряженную частицу, влетевшую в магнитное поле, действует сила F л, называется силой Лоренца. Она вычисляется в СИ по формуле F л = е u В sin a, где е – заряд частиц; u – её скорость; В – индукция магнитного поля, в котором движется частица; a – угол между направлением векторов скорости и индукции. Поскольку по условию задачи протон движется по замкнутой траектории (окружности), можно заключить, что составляющая вектора скорости в направлении вектора В равна нулю, т.е. a = 90°. Направление силы Лоренца подчиняется, как известно, правилу левой руки. Угол между направлениями е u В sin a = где т – масса протона; R – радиус окружности, по которой движется протон. Отсюда R = Протон получил скорость, пройдя ускоряющую разность потенциалов. По закону сохранения энергии работа, совершённая полем при перемещении протона, равна кинетической энергии, приобретённой протоном, т.е. А = Т. (2) Работа сил электрического поля при перемещении протона определяется по формуле А = еU. (3)
Кинетическая энергия протона Т = Подставив выражение А по (3) и выражение Т по (4) в (2), получим eU = откуда u = Подставляя выражение для u в (1), получим R = Проверим единицы величин правой и левой частей расчётной формулы, чтобы убедиться, что эти единицы совпадают. Для этого подставим в формулу вместо величин их единицы в Международной системе: м = Выпишем числовые значения в СИ и подставим их в (6): U = 400 В; е = 1,60·10–19 Кл (см. табл. 1); т = 1,67·10–27 кг (см. табл. 1); В = 0,2 Тл; a = p/2, sin a = 1; R =
Пример 5. Ток, текущий в рамке, содержащей N витков, создаёт магнитное поле. В центре рамки индукция В = 0,126 Тл. Найти магнитный момент рамки, если её радиус R = 10 см. Р е ш е н и е. Магнитный момент рамки с током р м = I S N, (1) где I – сила тока в рамке; S – площадь, охватываемая витком (S = p R 2); N – число витков в рамке. Индукция магнитного поля в центре кругового тока (многовиткового) В = откуда I = Подставляя в (1) выражения для I и S, получим р м = Выпишем числовые значения величин в СИ и подставим их в расчётную формулу (2): В = 0,126 Тл; R = 0,1 м; m0 = 4p·10–7 Гн/м; m = 1; р м =
Пример 6. Плоская рамка площадью S = 100 см2, содержащая N = 20 витков тонкого провода, вращается в однородном магнитном поле с индукцией В = 100 мТл. Амплитуда э.д.с. индукции Е max = 10 В. Определить частоту вращения рамки. Р е ш е н и е. Для определения частоты вращения рамки используем понятие угловой скорости вращения: w = где Т – период вращения; п – частота вращения. Отсюда п = Угловую скорость вращения найдём из соотношения Е = NBS w sin w t, (2) где Е – мгновенное значение э.д.с. индукции. Амплитудой Е является значение Е max, соответствующее значению sin w t = 1. Из соотношения (2) имеем w = Подставив выражение w по (3) в (1), получаем п = Выразим значения всех входящих в формулу, в СИ: Е max = 10 В; N = 20; В = 100 мТл = 0,1 Тл; S = 100 см2 = 10–2м2. п =
Пример 7. На немагнитный каркас длиной l = 50 см и площадью сечения S = 3 см2 намотан в один слой провод диаметром d = 0,4 мм так, что витки плотно прилегают друг к другу. Найти индуктивность получившегося соленоида и магнитный поток, пронизывающий поперечное сечение соленоида при токе I = 1 А. Р е ш е н и е. 1. Индуктивность соленоида вычисляется по формуле L = m0m n 2 V, (1) где п – число витков, приходящихся на единицу длины соленоида; V – объём соленоида.
Число витков п получим, разделив единицу длины на диаметр провода d: п = Объём соленоида V = Sl, где S – площадь поперечного сечения соленоида; l – длина соленоида. Подставим выражения для п и V в равенство (1): L = m0m Выпишем числовые значения в СИ и подставим их в расчётную формулу (3): l = 50 см = 0,5 м; S = 3 см2 = 3·10–4 м2; d = 0,4 мм = 4·10–4 м; m0 = 4p·10–7 Гн/м; m = 1; L = 4p·10–7 ·1 2. При наличии тока в соленоиде любое его поперечное сечение пронизывает магнитный поток Ф м = BS, (4) где В – магнитная индукция в соленоиде. Магнитная индукция соленоида определяется по формуле В = m0m I n. (5) Подставив выражения п и В по (2) и (5) в (4), получим расчётную формулу Ф м = m0m Выпишем вычисления, подставив в расчётную формулу значения величин I, S и d в СИ: Ф м = 4p·10–7 ·1
Пример 8. Колебательный контур состоит из плоского воздушного конденсатора с двумя пластинами площадью по S = 100 см2 каждая и катушки с индуктивностью L = 10–5 Гн. Период колебаний в контуре Т = 10–7 с. Определить расстояние между пластинами конденсатора. Р е ш е н и е. Искомое расстояние может быть найдено из формулы ёмкости плоского конденсатора С = где e0 – электрическая постоянная; e – диэлектрическая проницаемость среды между пластинами конденсатора; S – площадь пластины конденсатора; d – расстояние между пластинами. Отсюда d = Ёмкость С найдём из формулы Томсона, определяющий период колебаний Т в колебательном контуре, Т = 2p Отсюда С = Подставив это выражение С в (1), получим d = Выразим величины, входящие в это равенство в СИ и подставим их в расчётную формулу (2): L = 10–5 Гн; S = 100 см2 = 10–2 м2; Т = 10–7 с; e0 = 8,85·10–12 Ф/м; e = 1 (для воздуха); d = Пример 9. Длина железного сердечника тороида 40 см, длина воздушного зазора 1 см. Число витков N = 500. При какой величине тока индукция магнитного поля в зазоре будет равна 1,4 Тл. Р е ш е н и е. По закону полного тока циркуляция вектора напряженности по замкнутому контуру равна сумме токов, пронизывающих контур (рис. 2).
Потоком рассеяния пренебрегаем, магнитный поток в сердечнике и в зазоре будет одинаковым, а также одинаковой будет индукция магнитного поля: В 1 = В 2 = 1,4 Тл. Напряженность магнитного поля в зазоре:
Величины в единицах СИ: магнитная проницаемость μ 2 = 1 (для воздуха), магнитная постоянная μ 0 = 4π ∙ 10-7 Гн/м. Поставляем числовые значения Рис. 2 Напряженность поля в железном сердечнике находим по графику зависимости B от H (см. приложение). Для В = 1,4 Тл напряженность равна Н=0,8∙103А/м = 800 А/м. Тогда Величина тока равна:
IV. Оптика. Геометрическая оптика. КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОВЕРКИ УСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Каков диапазон длин волн видимого света? 2. Чему равна скорость движения фотонов? 3. Чем является свет – волной или частицей (корпускулой)? 4. Что называется оптически однородной средой? 5. Верно ли, что при переходе света из одной среды в другую длина световой волны l изменяется, а частота n остаётся неизменной? Объясните ответ. 6. Какое отражение света называют диффузным? 7. Каков физический смысл абсолютного показателя преломления среды? 8. Если с 1 и с 2 < с 1 – скорости света в первой и во второй средах, то какая из этих сред является оптически более плотной? 9. Какие два условия необходимы для полного отражения света от прозрачной среды? 10. Трёхгранная призма изготовлена из вещества с аномальной дисперсией. Какие лучи света данная призма отклоняет сильнее: красные или фиолетовые? 11. Что называют углом дисперсии? 12. Почему при прохождении белого света через трёхгранную призму происходит его разложение в спектр? 13. С помощью спектрометра можно получить спектр излучения любого вещества, находящегося в раскалённом состоянии. В каком случае этот спектр будет: 1) линейчатым; 2) полосатым; 3) сплошным? 14. На чём основан спектральный анализ? 15. Что называется фокусом линзы? Где он находится? 16. Фокусное расстояние линзы равно 25 см. Чему равна её оптическая сила? 17. Зависит ли фокусное расстояние f линзы от среды, в которой она находится? Можно ли, заменив окружающую среду, превратить собирающую линзу в рассеивающую? Объясните ответ. 18. Где и какое изображение даёт двояковыпуклая линза, если предмет находится за её двойным фокусом? Постройте это изображение. 19. Чем обусловлены сферическая и хроматическая аберрации линзы? Как можно устранить или уменьшить эти аберрации? 20. На каком расстоянии от объектива помещают предмет, рассматриваемый в микроскоп? 21. Какое изображение предмета даёт глаз и где оно помещается? 22. На какое расстояние аккомодирован глаз при расслабленной ресничной мышце? Каково расстояние ясного зрения для глаза? 23. Что называют предельным углом зрения невооружённого глаза? Чему он равен? 24. К свету какой длины волны (цвета) наиболее чувствителен глаз человека? 25. Что характеризует коэффициент видности? Дайте его определение. 26. Перечислите основные фотометрические характеристики и их единицы. Дайте определения этих характеристик и их единиц. 27. Что называют точечным источником света? 28. Во сколько раз освещённость в центре круглого стола больше, чем на его краю, на высоте, равной радиусу столешницы? 29. Объясните явление парникового эффекта. 30. Интенсивность света, прошедшего сквозь слой воды толщиной 4 м, уменьшилась в 2,72 раза. Чему равен коэффициент поглощения света для воды? 31. Какие реакции называют фотохимическими? 32. Что такое фотосинтез? Кратко охарактеризуйте его значение.
Волновая оптика.
КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОВЕРКИ УСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Почему нельзя получить интерференционную картину от двух светящихся тел, например от двух электроламп? 2. Для чего служит и как устроена оптическая система, называемая зеркалами Френеля? 3. Два когерентных луча с разностью хода в три световых волны интерферируют в некоторой точке. Что будет в этой точке: максимум или минимум освещённости? 4. Почему интерференционная картина, создаваемая на экране двумя когерентными источниками света, будет чёткой только при условии, что расстояние d между этими источниками гораздо меньше их расстояния L до экрана? 5. Почему радиоволны огибают здания и другие крупные объекты, а световые волны не огибают? 6. Что называют периодом (постоянной) дифракционной решётки? 7. Сколько штрихов на миллиметр должна иметь дифракционная решётка, пригодная для изучения инфракрасных спектров с длиной волны l порядка 102 мкм? 8. Объясните, почему при использовании белого света дифракционные максимумы становятся цветными (спектральными). Почему при этом только центральный максимум оказывается белым? 9. Почему разрешающая способность электронного микроскопа значительно больше, чем оптического микроскопа? 10. Протон и электрон движутся с одинаковой скоростью. Во сколько раз и какие волны длиннее: электронные или протонные? 11. Какой свет (луч) называют поляризованным? Чем он отличается от естественного света? 12. Интенсивность света, прошедшего сквозь поляризатор и анализатор, уменьшилась вдвое по сравнению с интенсивностью падающего естественного света. Какова взаимная ориентация поляризатора и анализатора (поглощение света в них пренебречь)? 13. Что происходит с обыкновенным лучом, падающим на слой канадского бальзама призмы Николя?
Квантовая оптика.
КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОВЕРКИ УСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Какой вид электромагнитного излучения является самым распространённым в природе? 2. Назовите количественные характеристики процессов испускания и поглощения, а также их единицы. Дайте определения этих характеристик и единиц. 3. У какого тела лучепоглощательная способность равна единице? 4. Сформулируйте закон Киргхофа. 5. Что называют спектральной плотностью энергетической светимости тела? 6. Поглощательная способность тела равна 0,8. Чему равна его испускательная способность, если испускательная способность абсолютно чёрного тела при той же температуре равна 5×107 Дж/(м2×с)? 7. Чему равно отношение кванта энергии излучения к частоте этого излучения? 8. С какой целью проводил Резерфорд опыты по рассеянию альфа-частиц? 9. Сформулируйте постулаты Бора. 10. Чему равна частота излучения атома водорода, соответствующая коротковолновой границе серии Лаймана? 11. Какие свойства – волновые или корпускулярные – обнаруживает свет в явлении фотоэффекта? 12. Сформулируйте три закона фотоэффекта и объясните второй и третий из них на основе квантовой теории света. 13. Чему равно отношение давлений света на зеркальную и чёрную поверхности? 14. Чему равно отношение импульса фотона к его частоте?
V. Физика атомного ядра.
КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОВЕРКИ УСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Сколько протонов и сколько нейтронов входит в состав ядра атома висмута? 2. Какой химический элемент имеет атомное ядро с символическим обозначением 3. Что называют массовым числом атома? 4. Охарактеризуйте a-, b- и g-излучения. 5. Каким способом можно замедлить процесс распада радиоактивного вещества? 6. Чему равны порядковый номер и массовое число изотопа, получающегося из 7. В каких единицах выражается постоянная распада? 8. Чему равна постоянная распада вещества, если среднее время жизни его атомов 0,1 мин? 9. Кем была осуществлена первая искусственная ядерная реакция? Какая это реакция (запишите её)? В чём заключалось её историческое значение? 10. Какие частицы являются более эффективными «снарядами» для «обстрела» атомных ядер при осуществлении ядерных реакций, a-частицы или нейтроны? Объясните ответ. 11. Чему равна удельная энергия связи ядра атома водорода (протия)? 12. Что называется критической массой ядерного горючего? 13. Изложите принцип устройства и действия ядерного уранового реактора на медленных нейтронах. 14. Почему термоядерная реакция (синтеза) может идти только при очень высокой температуре? 15. Какой из химических элементов выделяет наибольшую ядерную энергию при синтезе атомных ядер? 16. Какие частицы называют элементарными? 17. Какая из элементарных частиц имеет наименьшую массу покоя? Чему равен её электрический заряд? ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
Примеры решения задач
Пример 10. Лампа с силой света I = 50 кд расположена на расстоянии r = 1 м от лежащей на столе книги. Освещённость книги Е = 25 лк. Под каким углом падает свет на книгу? На какой высоте подвешена лампа над столом? Р е ш е н и е. Лампу можно принять за точечный источник света, так как её размеры малы в сравнении с расстоянием её до книги. Поэтому определить угол a, под которым падает свет, можно из формулы освещённости Е = где a – угол, под которым падают лучи (рис. 3). Из формулы (1) определим cos a:
Подставляем числовые значения величин в формулу (2) и вычисляем cos a = Следовательно, a = 60°. Рис. 3 Из рис. 3 видно, что высота лампы над столом h = r cos a = 1· 0,5 м = 0,5 м. Пример 11. Фокусное расстояние объектива микроскопа f 1 = 5 мм, окуляра f 2 = 25 мм. Предмет находится на расстоянии s = 5,1 мм от объектива (рис. 4). Вычислить длину тубуса микроскопа и даваемое микроскопом увеличение b. Р е ш е н и е. Увеличение микроскопа определяется по формуле b = b1 b2, (1) где b1 – увеличение, даваемое объективом; b2 – увеличение даваемое окуляром. b1 и b2 определяются по формулам b1 = b2 = где s ¢ – расстояние от объектива до даваемого им действительного изображения, см; 25 – расстояние наилучшего видения для нормального глаза, см. С учётом (2) и (3) формула (1) примет вид b =
Рис. 4
Расстояние s ¢ от объектива до изображения можно определить из формулы линзы
где s – расстояние от предмета до линзы. Откуда s ¢ = Вычислим s ¢: s ¢ = Выпишем числовые значения величин, входящих в формулу (4), и вычислим увеличение микроскопа: s ¢ = 25,5 см; f 1 = 5 мм = 0,5 см; f 2 = 25 мм = 2,5 см; b = Длину тубуса определим, исходя из следующих соображений. Действительное изображение, даваемое объективом, должно лежать почти в фокусе окуляра, так как окуляр действует как лупа (рис. 4). Поэтому длина тубуса L = s ¢ + f 2. (5) Подставив числовые значения в (5), вычислим длину тубуса L = 25,5 см + + 2,5 см = 28 см. Если принять, что L» s ¢, то для определения увеличения микроскопа можно также пользоваться приближённой формулой b = Подставив в эту формулу числовые значения, получим b =
Пример 12. Определить число штрихов на 1 мм дифракционной решётки, если при нормальном падении света длиной волны l = 600 нм решётка даёт первый максимум на расстоянии l = 3,3 см от центрального. Расстояние от решётки до экрана L = 110 см. Р е ш е н и е. Число штрихов N на 1 мм решётки определим по формуле N = где d – период решётки, т.е. расстояние между штрихами решётки. Период решётки найдём из формулы условия максимума d · sin j = k l, (2) где j – угол, под которым наблюдается k -й максимум (рис. 5); k – порядок (номер) максимума. Ввиду того, что для максимума 1-го порядка угол мал, можно принять sin j» tg j =
Рис. 5 Подставив в формулу (2) выражение синуса угла из (3), определим постоянную решётки d = С учётом (4) формула (1) примет вид N = Выпишем числовые значения, выразив их в СИ, и подставим в (5): l = 3,3 см = 3,3·10–2 м; L = 110 см = 1,10 м; k = 1; l = 600 нм = 600·10–9 м = 6·10–7 м; N =
Пример 13. Определить концентрацию С сахарного раствора, если при прохождении света через трубку с этим раствором длиной l = 20 см плоскость поляризации света поворачивается на угол j = 10°. Удельное вращение сахара в растворе [a] = 0,6 град/(дм∙%). Р е ш е н и е. Кон
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.046 с.) |

 = 2pn
= 2pn
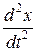 +
+  x = 0
x = 0




 = d T
= d T
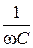



 ; U эф =
; U эф = 
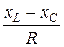

 Р е ш е н и е. На рис. 1 провода расположены перпендикулярно к плоскости чертежа. Маленькими кружочками изображены сечения проводов. Условимся, что ток I 1, течёт к нам (знак ·), а ток I 2 – от нас (знак Å). Общая индукция В в точке А равна векторной (геометрической) сумме индукции
Р е ш е н и е. На рис. 1 провода расположены перпендикулярно к плоскости чертежа. Маленькими кружочками изображены сечения проводов. Условимся, что ток I 1, течёт к нам (знак ·), а ток I 2 – от нас (знак Å). Общая индукция В в точке А равна векторной (геометрической) сумме индукции  и
и  полей, создаваемых каждым током в отдельности, т.е.
полей, создаваемых каждым током в отдельности, т.е. =
=  , (3)
, (3)
 . (4)
. (4)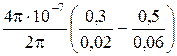 Тл = 1,33·10–6 Тл = 1,33 мкТл.
Тл = 1,33·10–6 Тл = 1,33 мкТл. .
. .
. . (2)
. (2) Тл = 1,01·10–3 Тл = 1,01 мТл.
Тл = 1,01·10–3 Тл = 1,01 мТл. . (2)
. (2) Тл = 0,052 Тл = 52 мТл.
Тл = 0,052 Тл = 52 мТл. и
и 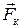 всегда составляет 90°. Следовательно, сила Лоренца является центростремительной силой, т.е. F л = F ц с или
всегда составляет 90°. Следовательно, сила Лоренца является центростремительной силой, т.е. F л = F ц с или ,
,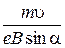 . (1)
. (1) . (4)
. (4) . (5)
. (5) . (6)
. (6) = м.
= м. м = 1,45·10–2 м = 1,45 см.
м = 1,45·10–2 м = 1,45 см. ,
, .
. . (2)
. (2) А·м2 = 6,3·102 А·м2 = 630 А·м2.
А·м2 = 6,3·102 А·м2 = 630 А·м2.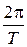 = 2p п,
= 2p п,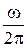 . (1)
. (1)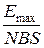 . (3)
. (3)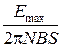 .
.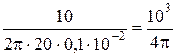 = 79,5 с–1.
= 79,5 с–1.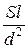 . (3)
. (3)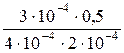 Гн = 1,17·10–3 Гн = 1,17 мГн.
Гн = 1,17·10–3 Гн = 1,17 мГн. .
.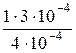 Вб = 9,42·10–7 Вб = 0,942 мкВб.
Вб = 9,42·10–7 Вб = 0,942 мкВб.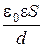 .
.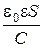 . (1)
. (1)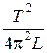 .
.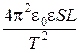 . (2)
. (2)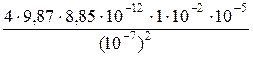 м = 3,49·10–3 м = 3,49 мм.
м = 3,49·10–3 м = 3,49 мм.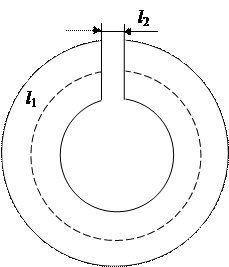
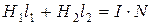
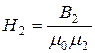
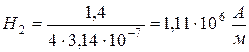 .
.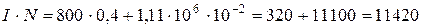 (А∙витков)
(А∙витков) (А)
(А)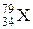 ?
?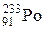 в результате двух a-распадов и одного b-распада?
в результате двух a-распадов и одного b-распада?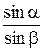 = п 21
= п 21
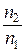
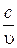
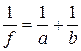
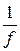
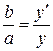
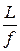
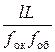
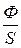
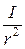 cos a
cos a
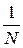
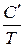
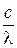
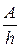 ; lгр =
; lгр = 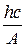
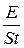
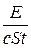 (1 + r)
(1 + r)
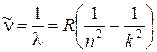
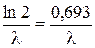
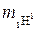 + (A – Z) mn – m я
+ (A – Z) mn – m я
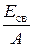
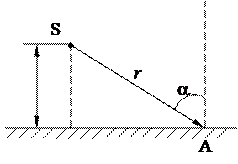 cos a =
cos a = 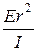 . (2)
. (2)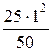 = 0,5.
= 0,5.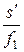 ; (2)
; (2)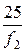 , (3)
, (3)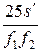 . (4)
. (4)
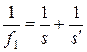 ,
,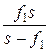 .
.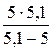 мм = 255 мм = 25,5 см.
мм = 255 мм = 25,5 см.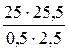 = 510.
= 510.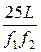 .
.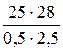 = 560.
= 560.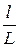 . (3)
. (3)
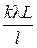 . (4)
. (4)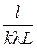 . (5)
. (5)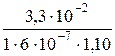 м–1 = 50 000 м–1 = 50 мм–1.
м–1 = 50 000 м–1 = 50 мм–1.


