
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории электромагнитного поля.Содержание книги
Поиск на нашем сайте
Вихревое электрическое поле Из электростатики мы знаем, что электрическое поле создается электрическими зарядами Q, cиловые линии такого поля не замкнуты, а циркуляция вектора Следовательно, электрическое поле Ток смещения Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями. Для электрического поля между обкладками можно записать теорему.Гаусса в виде:
Уравнения Максвелла в интегральной форме
Обобщение законов электромагнетизма было сделано в конце XIX в. Дж. К. Максвеллом в виде 4 уравнений. Он показал, что из этих уравнений можно вывести все основные формулы, описывающие электрические и магнитные явления в самых различных ситуациях. В основе теории электромагнитного поля Максвелла лежат два положения.
1. Всякое переменное магнитное поле порождает вихревое электрическое Поле.
2. Всякое изменяющееся во времени электрическое поле порождает вихревое магнитное поле.
Тогда полевые уравнения Максвелла в интегральной форме имеют вид:
Первое уравнение связывает значение скорости изменения магнитного потока через любую поверхность S и циркуляцию вектора напряженности электрического поля Второе уравнение устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем; оно указывает, что переменное электрическое поле приводит к появлению магнитного поля. Таким образом, мы должны считать, что магнитное поле создается не только токами проводимости, но и токами смещения. Это очень важный результат, так как токов проводимости может вообще не быть (например, в вакууме), но если есть электрическое поле и оно меняется со временем, то и в этом случае появляется магнитное поле. Это обобщенный закон Био-Савара-Лапласа..
Третье уравнение представляет собой теорему Гаусса в электростатике и указывает, что линии индукции электрического поля не замкнуты и что источником электростатического поля служат электрические заряды.
Четвертое уравнение представляеттеорему Гаусса для магнитного поля и указывает на то, что линии индукции магнитного поля являются замкнутыми, т.е., что в природе нет одиночных магнитных зарядов (монополей).
Из уравнений Максвелла следует, что электрическое и магнитное поля нельзя рассматривать как независимые, изменение во времени одного из этих полей приводит к появлению другого. Чтобы использовать уравнения Максвелла для расчета полей, к ним нужно еще добавить уравнения, характеризующие свойства среды (материальные уравнения), в которые входят диэлектрическая проницаемость ε, магнитная проницаемость μ и электропроводность σ среды. Для изотропных сред, не содержащих сегнетоэлектриков и ферромагнетиков.:
Последняя формула – это закон Ома в дифференциальной форме.
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ Незатухающие колебания Свободные (собственные) электрические колебания — колебания, совершающиеся без внешнего воздействия за счет первоначально накопленной энергии. Такие колебания совершаются в контуре, состоящем из катушки индуктивности L и конденсатора C. Если конденсатор предварительно зарядить, а потом подключить к катушке, то он будет разряжаться через катушку индуктивности. Ток разрядки создает магнитное поле в катушке. Магнитное поле, в свою очередь, за счет возникновения э.д.с. самоиндукции обеспечит перезарядку конденсатора. В каждый момент времени напряжения на катушке UL и конденсаторе UC равны друг другу, т.е. UC + UL=0. Тогда уравнение колебаний в таком контуре имеет вид: Решением его является q=q0·cos(ω0·t+φ0). Сила тока в цепи изменяется по закону I = – dq/dt = q0·ω0·sin(ω0·t + φ0) = I0· sin(ω0·t + φ0), где Полная энергия электромагнитных колебаний в контуре не изменяется с течением времени и равна:
Затухающие колебания Реальный колебательный контур имеет омическое сопротивление R, поэтому колебания в нем затухают, т.к. энергия, запасенная в контуре, выделяется в виде тепла. Уравнение затухающих колебаний в RLC -контуре имеет вид: В контуре возникнут колебания при условии:
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1586; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.254.103 (0.006 с.) |

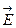 (обозначим его
(обозначим его 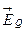 ) равна нулю:
) равна нулю: 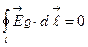 . С другой стороны, в явлении электромагнитной индукции изменяющееся магнитное поле приводит к э.д.с. εинд, т.е., к появлению электрического поля (обозначим его
. С другой стороны, в явлении электромагнитной индукции изменяющееся магнитное поле приводит к э.д.с. εинд, т.е., к появлению электрического поля (обозначим его  ),:
),:  . Сравнивая эти два выражения, видим, что между рассматриваемыми полями (
. Сравнивая эти два выражения, видим, что между рассматриваемыми полями (  .
.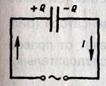 появление в окружающем пространстве вихревого магнитного поля. Согласно Максвеллу, конденсатор является для постоянного тока разрывом цепи, через него ток не протекает, однако, в цепи переменного тока, содержащей конденсатор (рис.), электрический ток протекает и приборы фиксируют наличие магнитного поля у проводников с током, но оказалось, что возникает и магнитное поле между обкладками конденсатора, хотя там нет движения зарядов. А что там есть? Переменное электрическое поле вследствие постоянной перезарядки конденсатора. Вот это переменное электрическое поле, приводящее к возникновению магнитного поля Максвелл назвал «током смещения». Подчеркнем, что из всех свойств, присущих току проводимости, он приписал току смещения лишь одно − способность создавать в окружающем пространстве магнитное поле.
появление в окружающем пространстве вихревого магнитного поля. Согласно Максвеллу, конденсатор является для постоянного тока разрывом цепи, через него ток не протекает, однако, в цепи переменного тока, содержащей конденсатор (рис.), электрический ток протекает и приборы фиксируют наличие магнитного поля у проводников с током, но оказалось, что возникает и магнитное поле между обкладками конденсатора, хотя там нет движения зарядов. А что там есть? Переменное электрическое поле вследствие постоянной перезарядки конденсатора. Вот это переменное электрическое поле, приводящее к возникновению магнитного поля Максвелл назвал «током смещения». Подчеркнем, что из всех свойств, присущих току проводимости, он приписал току смещения лишь одно − способность создавать в окружающем пространстве магнитное поле. . Если возьмем производную по времени от этого выражения, то получим величину, имеющую размерность силы тока, это и есть ток смещения IСМ:
. Если возьмем производную по времени от этого выражения, то получим величину, имеющую размерность силы тока, это и есть ток смещения IСМ: 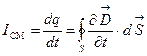 , где величина, характеризующая быстроту изменения электрического поля в конденсаторе
, где величина, характеризующая быстроту изменения электрического поля в конденсаторе 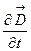 , имеет смысл плотности тока смещения
, имеет смысл плотности тока смещения  . Таким образом, согласно Максвеллу, магнитное поле создается не только токами проводимости IПРОВ, но и переменными электрическими полями. Поэтому теорему о циркуляции вектора
. Таким образом, согласно Максвеллу, магнитное поле создается не только токами проводимости IПРОВ, но и переменными электрическими полями. Поэтому теорему о циркуляции вектора 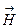 можно записать как:
можно записать как: .
.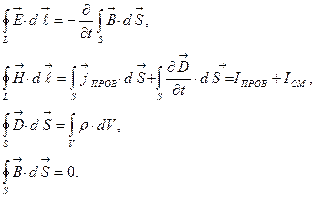

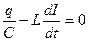 . Если учесть, что заряд на конденсаторе q и ток в цепи I связаны соотношением I = − dq/dt (уменьшение заряда на конденсаторе приводит к возрастанию тока в цепи и наоборот), приходим к уравнению свободных гармонических незатухающих колебаний:
. Если учесть, что заряд на конденсаторе q и ток в цепи I связаны соотношением I = − dq/dt (уменьшение заряда на конденсаторе приводит к возрастанию тока в цепи и наоборот), приходим к уравнению свободных гармонических незатухающих колебаний: 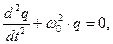 где частота собственных колебаний:
где частота собственных колебаний: 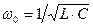
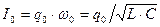 – амплитуда тока. При свободных гармонических колебаниях в колебательном контуре происходит периодическое преобразование энергии We электрического поля конденсатора в энергию магнитного поля Wm катушки и наоборот:
– амплитуда тока. При свободных гармонических колебаниях в колебательном контуре происходит периодическое преобразование энергии We электрического поля конденсатора в энергию магнитного поля Wm катушки и наоборот: 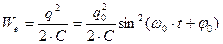 ;
; 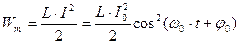 .
. .
. где β=R /(2· L) – коэффициент затухания.
где β=R /(2· L) – коэффициент затухания.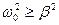 , т.е., при L > C·R2/4. Решение уравнения колебаний имеет вид:
, т.е., при L > C·R2/4. Решение уравнения колебаний имеет вид:  , где
, где  Затухание колебаний характеризуют логарифмическим декрементом затухания
Затухание колебаний характеризуют логарифмическим декрементом затухания  и добротностью
и добротностью 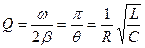 . Если значение индуктивности L ≤ C·R2/4, то э.д.с. самоиндукции оказывается недостаточной, чтобы вызвать перезарядку обкладок конденсатора, процесс будет апериодическим. Сопротивление контура, при котором колебательный процесс переходит в апериодический (ω0 = β), называется критическим:
. Если значение индуктивности L ≤ C·R2/4, то э.д.с. самоиндукции оказывается недостаточной, чтобы вызвать перезарядку обкладок конденсатора, процесс будет апериодическим. Сопротивление контура, при котором колебательный процесс переходит в апериодический (ω0 = β), называется критическим: 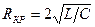 .
.


