
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы сохранения в механике.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любое тело или совокупность тел можно рассматривать как систему материальных точек. Состояние системы характеризуется заданием координат и импульсов всех ее частей. Зная законы действующих в системе сил и состояние системы в начальный момент, можно с помощью дифференциальных уравнений динамики определить состояние системы в любой момент времени. Но часто ввиду сложности систем и процессов, происходящих в них, невозможно до конца провести подобное решение. В системе взаимодействующих тел координаты, скорости и ускорения тел постоянно меняются. Однако, существуют три физические величины, которые в замкнутой системе (системе не взаимодействующей с внешними телами) остаются неизменными (сохраняются). Такими величинами являются импульс, энергия и момент импульса (об этой величине ниже). Особенно важная роль этих величин связана с тем, что они являются аддитивными: их значения для системы, состоящей из частей, равно сумме значений для каждой из частей в отдельности. Закон сохранения механической энергии: в инерциальной системе отсчета полная механическая энергия замкнутой системы частиц, в которой действуют только консервативные силы, сохраняется: E = ЕКИН + ЕПОТ = const. Сохраняется именно полная механическая энергия, в то время как кинетическая и потенциальная энергии по отдельности могут меняться. В основе закона сохранения механической энергии лежит свойство однородности времени, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора начала отсчета времени. Например, потенциальная энергия поднятого на некоторую высоту тела не меняется с течением времени. Если бы это было не так, то можно было бы поднять тело, дождаться момента, когда его энергия увеличится, и заставить тело совершить работу. Мы получили бы вечный двигатель, работающий за счет разности энергий: возросшей с течением времени и затраченной на подъем тела. Закон сохранения импульса: в инерциальной системе отсчета импульс замкнутой системы частиц остается постоянным как по величине, так и по направлению, т.е. Действительно, из уравнения движения При этом импульсы отдельных частей системы могут меняться. У незамкнутой системы может сохраняться не сам импульс, а его проекция на то направление, по которому сумма проекций действующих сил равна нулю. В основе закона сохранения импульса лежит свойство однородности пространства, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора положения начала координат. Если бы пространство было неоднородным, т.е. точки пространства были бы неэквивалентны, то при движении свободного тела эта неэквивалентность проявилась бы в изменении импульса (появлении ускорения). С помощью законов сохранения можно, не решая уравнений динамики, сделать во многих случаях ряд заключений о свойствах процессов, не вникая в их детальное рассмотрение. Законы сохранения представляют собой общие фундаментальные принципы и отражают свойства пространства и времени.
МЕХАНИКА ТВЕРДОГО ТЕЛА.
Кинетическая энергия вращения. Момент инерции материальной точки и тела относительно неподвижной оси. Пусть материальная точка массой m движется вокруг некоторой оси по окружности радиуса r со скоростью υ. Тогда кинетическую энергию точки с учетом связи линейной и угловой скоростей υ =ω·r можно записать так:
Моментом инерции тела относительно оси называется сумма моментов инерции элементов (материальных точек), из которых состоит тело: Момент инерции сплошного тела определяют интегрированием по всему объему (по всем материальным точкам): Если тело имеет плотность ρ, то последнее равенство можно представить в виде:
Момент инерции сплошного цилиндра массой т и радиуса основания R относительно оси, проходящей через центр масс цилиндра параллельно его образующей, рассчитанный по этой формуле, равен: Для сплошного шара массой т и радиуса R момент инерции относительно оси, проходящей через центр масс шара, равен: Момент инерции для стержня длиной ℓ и массой т относительно оси, проходящей через центр масс стержня перпендикулярно ему,: Момент инерции J тела характеризует, с одной стороны, инертные свойства тела при вращательном движении, а с другой стороны, распределение вещества в пространстве относительно оси. Момент инерции, так же как и масса тела, является аддитивной величиной. Если известен момент инерции Jo тела относительно оси, проходящей через центр масс тела, то можно найти его момент инерции относительно любой другой параллельной ей оси: J = J0 + m·d 2, где d – расстояние между осями. Последнее равенство выражает теорему Штейнера: момент инерции относительно любой оси вращения равен моменту инерции относительно параллельной оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения. Из теоремы Штейнера очевидно, что всегда J>J0, т.е. минимальное значение момента инерции достигается для оси, проходящей через центр масс. Единицей момента инерции в системе СИ служит 1 кг·м2. Если тело катится, то кинетическая энергия такого тела определяется поступательным движением тела как целого и вращением относительно движущейся оси:
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 704; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.009 с.) |

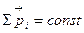 .
. следует для замкнутой системы (
следует для замкнутой системы ( ), что импульс системы
), что импульс системы 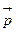 остается постоянным.
остается постоянным.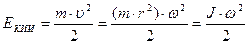 , где величина J=m·r2 называется моментом инерции материальной точки.
, где величина J=m·r2 называется моментом инерции материальной точки. .
. .
. , где учтено, что d т= ρ·dV.
, где учтено, что d т= ρ·dV. .
.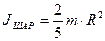 .
. .
. .
.


