
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый постулат (принцип относительности): все законы физики имеют одинаковую форму во всех инерциальных системах отсчета (ИСО).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
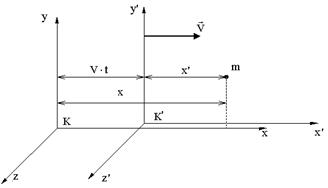
Пусть система отсчета K является неподвижной, а система K’ движется относительно нее вдоль оси x со скоростью υ. Уравнения преобразования координат и времени для т. m при переходе от одной ИСО к другой, полученные Лоренцем, имеют вид:
Следствия из преобразований Лоренца. 1. Сокращение длины. Пусть вдоль оси x’ в движущейся системе отсчета K’ лежит стержень длины ℓ o (это собственная длина или длина предмета (стержня) в той системе отсчета, в которой он покоится). Тогда ℓ – длина стержня относительно неподвижной системы отсчета K – равна: Таким образом, движущийся предмет кажется наблюдателю более коротким, чем покоящийся. Сокращение происходит только в направлении относительного движения и становится заметным лишь при υ, близкой к скорости света в вакууме с. 2. Замедление времени. где Δ t0 – собственное время, т.е. промежуток времени в системе, где часы покоятся, Δ t соответствует промежутку времени в системе, относительно которой часы движутся, причем Δ t > Δ t0. Таким образом, движущиеся часы идут медленнее покоящихся. 3. Относительность одновременности. События, одновременные в одной ИСО, оказываются неодновременными по отношению к другой ИСО. 4. Релятивистские формулы преобразования скоростей (закон сложения скоростей) получаются дифференцированием по времени преобразований Лоренца:
Здесь их, иу, uz, u’x, u ’ y и и'г — проекции скорости движущейся частицы на оси неподвижной и подвижной систем отсчета, соответственно. Отсюда следует, что скорость света, равная u’x = с относительно системы отсчета K’, и относительно K будет равна их = с. Физические величины, которые не меняются при переходе от одной инерциальной системы к другой, называются инвариантами теории относительности. К инвариантам, например, относятся скорость света в вакууме, масса и электрический заряд частицы, пространственно-временной интервал А. Эйнштейн показал, что закон природы – основное уравнение динамики Из этой формулы видно, что тело, обладающее массой, не может двигаться со скоростью, большей или равной скорости света с. Из этой же формулы следует, что со скоростью света может двигаться, обладая конечным импульсом, только безмассовая частица (m =0). Это, например, фотон. Основное уравнение динамики в СТО принимает, т.о., вид:
Если сила Если истолковывать
Согласно СТО, пространство и время являются относительными, зависят друг от друга, образуя единый 4-х мерный пространственно-временной континуум. Несколько позже в общей теории относительности А. Эйнштейн показал, что на пространство и время влияет тяготение, а именно, вблизи очень массивных тел пространство искривляется, а время замедляется. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
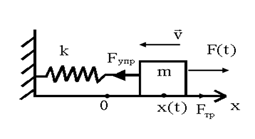
Свободные (собственные) колебания –колебания, происходящие без внешних воздействий за счет первоначально полученной телом энергии. Рассмотрим горизонтальный пружинный маятник жесткостью k и массой m, помещенный в среду с коэффициентом сопротивления r, на который вдоль оси х действует переменная внешняя сила F(t), изменяющаяся со временем, например, по гармоническому закону F(t) = F0 · cosΩt с некоторой частотой Ω. Уравнение движения маятника:
где введены обозначения Проанализируем уравнение (2).
1. Свободные гармонические незатухающие колебания.
Его решением является гармоническая функция: в чем легко убедиться, подставив (4) в (3). В (4) xm, ω 0 и φ0 – постоянные величины. xm – амплитуда – величина, указывающая максимальное значение координаты х при отклонении от положения равновесия, ω 0 – собственная частота, аргумент косинуса Частота колебаний зависит только от свойств колеблющейся системы, но не от амплитуды, а амплитуда и начальная фаза колебаний определяются начальными условиями ее движения, выводящими систему из состояния покоя. Скорость колеблющейся частицы равна: Ускорение частицы при таком движении: Складывая кинетическую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы:
Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потенциальная энергии изменяются со временем, как sin2(ω0·t + φ0) и cos2(ω0·t + φ0), так что когда одна из них увеличивается, другая – уменьшается, т.е. процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения частицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x, действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса). Примечание: В механике обычно рассматривают колебания: – математического маятника с периодом – физического маятника с периодом – пружинного маятника с периодом
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.183.161 (0.009 с.) |

 Второй постулат (постоянство скорости света): свет распространяется в пустом пространстве со скоростью с = 3·108 м/с, не зависящей от скорости движения источника или наблюдателя.
Второй постулат (постоянство скорости света): свет распространяется в пустом пространстве со скоростью с = 3·108 м/с, не зависящей от скорости движения источника или наблюдателя.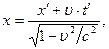



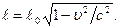
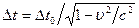 ,
, 
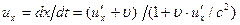 ;
;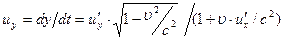 ;
;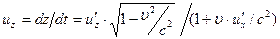 .
.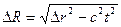 .
.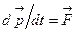 – будет инвариантен к преобразованиям Лоренца, если импульс тела
– будет инвариантен к преобразованиям Лоренца, если импульс тела 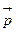 будет иметь вид:
будет иметь вид: 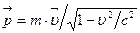 .
.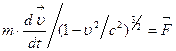 .
.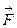 совершает работу, разгоняя тело от нулевой скорости до некоторой релятивистской скорости
совершает работу, разгоняя тело от нулевой скорости до некоторой релятивистской скорости 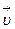 , то эта работа целиком идет на создание кинетической энергии, т.е.:
, то эта работа целиком идет на создание кинетической энергии, т.е.: 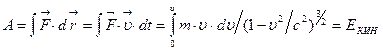 . Вычисление интеграла приводит к выражению:
. Вычисление интеграла приводит к выражению:  .
.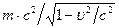 как полную энергию
как полную энергию  тела, то отсюда следует, что когда тело покоится и его кинетическая энергия равна нулю, оно тем не менее обладает энергией т·с2. В соответствии с этим т·с2 называют энергией покоя тела: Е0 = m·c2. Это знаменитая формула Эйнштейна, говорящая о том, что масса тела является не только мерой инертности или мерой гравитационного действия, но и мерой энергосодержания тела. Используя выражения для импульса и энергии тела можно получить еще одно часто используемое выражение для полной энергии тела:
тела, то отсюда следует, что когда тело покоится и его кинетическая энергия равна нулю, оно тем не менее обладает энергией т·с2. В соответствии с этим т·с2 называют энергией покоя тела: Е0 = m·c2. Это знаменитая формула Эйнштейна, говорящая о том, что масса тела является не только мерой инертности или мерой гравитационного действия, но и мерой энергосодержания тела. Используя выражения для импульса и энергии тела можно получить еще одно часто используемое выражение для полной энергии тела: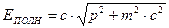 .
. Движение, которое повторяется через равные промежутки времени, называется колебательным. Промежуток времени T, по истечение которого движение повторяется, называется периодом колебания. В моменты времени t и t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/ Т. Она определяет, сколько раз в секунду повторяется движение, и измеряется в герцах (Гц). Круговой (циклической) частотой называется величина ω = 2 π v.
Движение, которое повторяется через равные промежутки времени, называется колебательным. Промежуток времени T, по истечение которого движение повторяется, называется периодом колебания. В моменты времени t и t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/ Т. Она определяет, сколько раз в секунду повторяется движение, и измеряется в герцах (Гц). Круговой (циклической) частотой называется величина ω = 2 π v.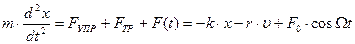 (1), где сила упругости FУПР пропорциональна смещению х, а сила трения (сопротивления) FТР среды – скорости υ= dx/dt. Перепишем (1) по другому:
(1), где сила упругости FУПР пропорциональна смещению х, а сила трения (сопротивления) FТР среды – скорости υ= dx/dt. Перепишем (1) по другому: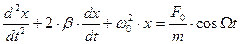 (2),
(2),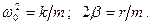
 Маятник в отсутствие силы трения (r =0) и внешней силы (F0= 0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:
Маятник в отсутствие силы трения (r =0) и внешней силы (F0= 0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид: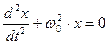 (3).
(3).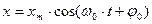 (4),
(4),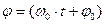 носит название фазы колебания; φ0 — начальная фаза колебания (в момент t = 0).
носит название фазы колебания; φ0 — начальная фаза колебания (в момент t = 0).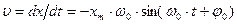 (5).
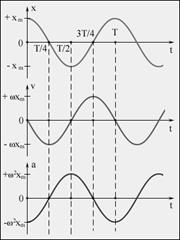
(5).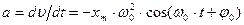 (6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0 =0.
(6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0 =0.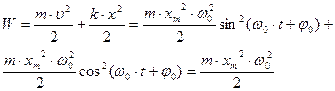 (7).
(7). , где ℓ– длина маятника;
, где ℓ– длина маятника; , где J– момент инерции маятника, a – расстояние от точки подвеса маятника до его центра масс;
, где J– момент инерции маятника, a – расстояние от точки подвеса маятника до его центра масс; , где k– жесткость пружины.
, где k– жесткость пружины.


