
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухатомные молекулы. Схема энергетических уровней. Комбинационное рассеяние света.Содержание книги
Поиск на нашем сайте
Молекула – это наименьшая частица вещества, состоящая из одинаковых или различных атомов, соединенных химическими связями, и являющаяся носителем его основных химических и физических свойств. Преимущественно можно говорить о двух типах химической связи: ионной (гетерополярной) и ковалентной (гомеополярной). Ионная связь осуществляется благодаря кулоновскому притяжению между разноименно заряженными ионами (например, молекулы NaCl, КВг), а ковалентная – в результате обменного взаимодействия, носящего чисто квантовый характер и не имеющего аналога в классической физике (например, молекулы Н2, СО). Число атомов, составляющих молекулы, может быть от двух – двухатомные молекулы (Н2, СО, КС1) – до сотен и тысяч – многоатомные молекулы (белки,...). Простейшая молекула с ковалентной связью – молекула водорода – состоит из двух протонов (ядер атома водорода) и двух электронов. Ковалентная связь объясняется принципом неразличимости тождественных частиц. Между двумя электронами (а они являются тождественными частицами) наблюдается обменное взаимодействие, возникающее как бы за счет обмена валентными электронами между двумя атомами. При сближении двух водородных атомов до расстояний порядка боровского радиуса (при обязательном условии антипараллельности спинов валентных электронов) возникает их взаимное притяжение и образуется устойчивая молекула водорода. Состояние молекулы как квантовой системы описывается уравнением Шредингера, учитывающим взаимодействие электронов с ядрами, электронов друг с другом, а также кинетическую энергию электронов и ядер. Для приближенного решения этой задачи (довольно сложной) используют адиабатное приближение, согласно которому квантово-механическая система разделяется на тяжелые и легкие частицы – ядра и электроны. Так как массы и скорости этих частиц сильно различаются, то считается, что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле электронов. Следовательно, в адиабатном приближении уравнение Шредингера для молекулы распадается на два уравнения – для электронов и ядер. Полная энергия молекулы без учета энергии поступательного движения (она не квантуется, поэтому ее изменения не приводят к возникновению дискретного спектра) и энергии ядер (она обусловливает только сверхтонкую структуру спектральных линий)
где Еэл – энергия, обусловленная движением электронов относительно ядер, Екол – энергия, обусловленная колебанием ядер (учитывает периодически изменяющееся относительное положение ядер), Eвр – энергия, обусловленная вращением ядер (учитывает периодически изменяющуюся ориентацию молекулы в пространстве). Каждая из входящих в выражение (169) энергий квантуется (ей соответствует набор дискретных уровней энергии) и определяется квантовыми числами. Отношения
где т – масса электрона, М имеет порядок массы ядер; Приближенная квантовая модель молекулы [см. (169) и рис. 86] – это совокупность далеко отстоящих друг от друга электронных уровней (различные Еэл при Екол = Евр = 0), довольно близко расположенных друг к другу колебательных уровней (заданное Еэл при различных Екол и Евр = 0) и еще более близких друг к другу вращательных уровней (заданные Еэл и Екол при различных Евр). Молекулярные спектры – спектры излучения (поглощения), возникающие при квантовых переходах между уровнями энергии молекул. Спектр излучения (поглощения) молекулы определяется: 1) структурой ее энергетических уровней; 2) правилами отбора (например, изменение квантовых чисел, отвечающих как колебательному, так и вращательному движению, равно ± 1). Спектр молекул довольно сложный. Различают электронные спектры (соответствуют переходам с одного электронного уровня на другой), колебательные спектры (соответствуют переходам с одного колебательного уровня на другой), вращательные спектры (соответствуют переходам с одного вращательного уровня на другой); кроме того, возможны еще электронно-колебательные и колебательно-вращательные спектры. Итак, при разных типах переходов между уровнями (при обязательном соблюдении правил отбора) возникают различные типы молекулярных спектров. Молекулярные спектры за их характерный вид называют полосатыми. Это совокупность более или менее узких полос в ультрафиолетовой, видимой и инфракрасной областях. В 1928 г. академики Г. С. Ландсберг (1890—1957) и Л. И. Мандельштам и одновременно индийские физики Ч. Раман (1888—1970) и К. Кришнан (р. 1911) открыли явление комбинационного рассеяния света. Если на вещество (газ, жидкость, прозрачный кристалл) падает строго монохроматический свет, то в спектре рассеянного света помимо несмещенной спектральной линии обнаруживаются новые линии, частоты которых представляют собой суммы или разности частоты n падающего света и частот ni собственных колебаний (или вращений) молекул рассеивающей среды. Линии в спектре комбинационного рассеяния с частотами n – ni, меньшими частоты n падающего света, называются стоксовыми (или красными) спутниками, линии с частотами n + ni, большими n, — антистоксовыми (или фиолетовыми) спутниками. Анализ спектров комбинационного рассеяния приводит к следующим выводам: 1) линии спутников располагаются симметрично по обе стороны от несмещенной линии; 2) частоты ni не зависят от частоты падающего на вещество света, а определяются только рассеивающим веществом, т. е. характеризуют его состав и структуру; 3) число спутников определяется рассеивающим веществом; 4) интенсивность антистоксовых спутников меньше интенсивности стоксовых и с повышением температуры рассеивающего вещества увеличивается, в то время как интенсивность стоксовых спутников практически от температуры не зависит. Объяснение закономерностей комбинационного рассеяния света дает квантовая теория. Согласно этой теории, рассеяние света есть процесс, в котором один фотон поглощается и один фотон испускается молекулой. Если энергии фотонов одинаковы, то в рассеянном свете наблюдается несмещенная линия. Однако возможны процессы рассеяния, при которых энергии поглощенного и испущенного фотонов различны. Различие энергии фотонов связано с переходом молекулы из нормального состояния в возбужденное (испущенный фотон будет иметь меньшую частоту — возникает стоксов спутник) либо из возбужденного состояния в нормальное (испущенный фотон будет иметь большую частоту — возникает антистоксов спутник). Рассеяние света сопровождается переходами молекулы между различными колебательными или вращательными уровнями, в результате чего и возникает ряд симметрично расположенных спутников. Число спутников, таким образом, определяется энергетическим спектром молекул, т. е. зависит только от природы рассеивающего вещества. Так как число возбужденных молекул гораздо меньше, чем число невозбужденных, то интенсивность антистоксовых спутников меньше, чем стоксовых. С повышением температуры число возбужденных молекул растет, в результате чего возрастает и интенсивность антистоксовых спутников. Молекулярные спектры (в том числе и спектры комбинационного рассеяния света) применяются для исследования строения и свойств молекул, используются в молекулярном спектральном анализе, лазерной спектроскопии, квантовой электронике и т. д.
Билет 41 Теплоемкость твердых тел В качестве модели твердого тела рассмотрим правильно построенную кристаллическую решетку, в узлах которой частицы (атомы, ионы, молекулы), принимаемые за материальные точки, колеблются около своих положений равновесия — узлов решетки — в трех взаимно перпендикулярных направлениях. Таким образом, каждой составляющей кристаллическую решетку частице приписывается три колебательных степени свободы, каждая из которых, согласно закону равнораспределения энергии по степеням свободы (см. § 50), обладает энергией kT. Внутренняя энергия моля твердого тела
где NA— постоянная Авогадро; NAk=R (R — молярная газовая постоянная). Молярная теплоемкость твердого тела
т. е. молярная (атомная) теплоемкость химически простых тел в кристаллическом
состоянии одинакова (равна 3 R) и не зависит от температуры. Этот закон был эмпирически получен французскими учеными П. Дюлонгом (1785—1838) и Л. Пти (1791—1820) и носит название закона Дюлонга и Пти. Если твердое тело является химическим соединением (например, NaCl), то число частиц в моле не равно постоянной Авогадро, а равно nNA, где n — число атомов в молекуле (для NaCl число частиц в моле равно 2 NA, так, в одном моле NaCl содержится NA атомов Na и NA атомов Cl). Таким образом, молярная теплоемкость твердых химических соединений
т. е. равна сумме атомных теплоемкостей элементов, составляющих это соединение. Как показывают опытные данные (табл. 4), для многих веществ закон Дюлонга и Пти выполняется с довольно хорошим приближением, хотя некоторые вещества (С, Be, В) имеют значительные отклонения от вычисленных теплоемкостей. Кроме того, так же как и в случае газов (см. § 53), опыты по измерению теплоемкости твердых тел при низких температурах показали, что она зависит от температуры (рис. 113). Вблизи нуля кельвин теплоемкость тел пропорциональна Т 3, и только при достаточно высоких температурах, характерных для каждого вещества, выполняется условие (73.1). Алмаз, например, имеет теплоемкость, равную 3 R при1800 К! Однако для большинства твердых тел комнатная температура является уже достаточно высокой. Таблица 4
Расхождение опытных и теоретических значений теплоемкостей, вычисленных на основе классической теории, объяснили, исходя из квантовой теории теплоемкостей, А. Эйнштейн и П. Дебай. Билет 42 Понятие о квантовой теории теплоемкости. Фононы Квантовая статистика устранила трудности в объяснении зависимости теплоемкости газов (в частности, двухатомных) от температуры (см. § 53). Согласно квантовой механике, энергия вращательного движения молекул и энергия колебаний атомов в молекуле могут принимать лишь дискретные значения. Если энергия теплового движения значительно меньше разности энергий соседних уровней энергии (kT <<D E), то при столкновении молекул вращательные и колебательные степени свободы практически не возбуждаются. Поэтому при низких температурах поведение двухатомного газа подобно одноатомному. Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными, т. е. D E вращ<<D E кол (см. § 230), то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоемкость возрастает; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоемкости (см. рис. 80). Функции распределения Ферми — Дирака для T =0 К и T >0 заметно различаются (рис. 312) лишь в узкой области энергий (порядка kT). Следовательно, в процессе нагревания металла участвует лишь незначительная часть всех электронов проводимости.Этим и объясняется отсутствие заметной разницы между теплоемкостями металлов и диэлектриков, что не могло быть объяснено классической теорией (см. § 103). Как уже указывалось (см. § 73), классическая теория не смогла объяснить также зависимость теплоемкости твердых тел от температуры, а квантовая статистика решила эту задачу. Так, А. Эйнштейн, приближенно считая, что колебания атомов кристаллической решетки независимы (модель кристалла как совокупности независимых колеблющихся с одинаковой частотой гармонических осцилляторов), создал качественную квантовую теорию теплоемкости кристаллической решетки. Она впоследствии была развита П. Дебаем, который учел, что колебания атомов в кристаллической решетке не являются независимыми (рассмотрел непрерывный спектр частот гармонических осцилляторов). Рассматривая непрерывный спектр частот осцилляторов, П. Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле. Согласно корпускулярно-волновому дуализму свойств вещества, упругим волнам в кристалле сопоставляют фононы, обладающие энергией Е= Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (например, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке — он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе. Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе — Эйнштейна (см. § 235), так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным; поэтому в формуле (235.1) для фононов необходимо m положить равным нулю. Применение статистики Бозе — Эйнштейна к фононному газу — газу из невзаимодействующих бозе-частиц — привело П. Дебая к количественному выводу, согласно которому при высоких температурах, когда T >> T D (классическая область), теплоемкость твердых тел описывается законом Дюлонга и Пти (см. § 73), а при низких температурах, когда T << T D (квантовая область), — пропорциональна кубу термодинамической температуры: СV~Т 3. В данном случае TD — характеристическая температура Дебая, определяемая соотношением kТD= Модель квазичастиц — фононов — оказалась эффективной для объяснения открытого П. Л. Капицей явления сверхтекучести жидкого гелия (см. § 31, 75). Теория сверхтекучести, созданная (1941) Л. Д. Ландау и развитая (1947) российским ученым Н. Н. Боголюбовым (р. 1909), применена впоследствии к явлению сверхпроводимости (см. § 239). Билет 43 Размер, состав и заряд атомного ядра. Массовое и зарядовое числа Э. Резерфорд, исследуя прохождение a-частиц с энергией в несколько мегаэлектрон-вольт через тонкие пленки золота (см. § 208), пришел к выводу о том, что атом состоит из положительно заряженного ядра и окружающих его электронов. Проанализировав эти опыты, Резерфорд также показал, что атомные ядра имеют размеры примерно 10–14 — 10–15 м (линейные размеры атома примерно 10–10 м). Атомное ядро состоит из элементарных частиц — протонов и нейтронов (протонно-нейтронная модель ядра была предложена российским физиком Д. Д. Иваненко (р. 1904), а впоследствии развита В. Гейзенбергом). Протон (р) имеет положительный заряд, равный заряду электрона, и массу покоя тр= 1,6726×10–27кг» 1836 тe, где тe — масса электрона. Нейтрон (n) — нейтральная частица с массой покоя тп= 1,6749×10–27кг»1839 тe. Протоны и нейтроны называются нуклонами (от лат. nucleus — ядро). Общее число нуклонов в атомном ядре называется массовым числом А. Атомное ядро характеризуется зарядом Ze, где Z — зарядовое число ядра, равное числу протонов в ядре и совпадающее с порядковым номером химического элемента в Периодической системе элементов Менделеева. Известные в настоящее время 107 элементов таблицы Менделеева имеют зарядовые числа ядер от Z = 1 до Z = 107. Ядро обозначается тем же символом, что и нейтральный атом: Сейчас протонно-нейтронная модель ядра не вызывает сомнений. Рассматривалась также гипотеза о протонно-электронном строении ядра, но она не выдержала экспериментальной проверки. Так, если придерживаться этой гипотезы, то массовое число А должно представлять собой число протонов в ядре, а разность между массовым числом и числом электронов должна быть равна зарядовому числу. Эта модель согласовывалась со значениями изотопных масс и зарядов, но противоречила значениям спинов и магнитных моментов ядер, энергии связи ядра и т. д. Кроме того, она оказалась несовместимой с соотношением неопределенностей (см. § 215). В результате гипотеза о протонно-электронном строении ядра была отвергнута. Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. От числа же электронов зависит их распределение по состояниям в атоме, от которого, в свою очередь, зависят химические свойства атома. Следовательно, заряд ядра определяет специфику данного химического элемента, т.е. определяет число электронов в атоме, конфигурацию их электронных оболочек, величину и характер внутриатомного электрического поля. Ядра с одинаковыми Z, но разными А (т. е. с разными числами нейтронов N=A–Z) называются изотопами, а ядра с одинаковыми А, но разными Z — изобарами. Например, водород (Z =1) имеет три изотопа: Радиус ядра задается эмпирической формулой
где R 0 = (1,3¸1,7)10–15 м. Однако при употреблении этого понятия необходимо соблюдать осторожность (из-за его неоднозначности, например из-за размытости границы ядра). Из формулы (251.1) вытекает, что объем ядра пропорционален числу нуклонов в ядре. Следовательно, плотность ядерного вещества примерно одинакова для всех ядер (»1017 кг/м3).
Спин ядра и его магнитный момент Использование приборов высокой разрешающей способности и специальных источников возбуждения спектра позволило обнаружить сверхтонкую структуру спектральных линий. Ее существование В. Паули объяснил (1924) наличием у атомных ядер собственного момента импульса (спина) и магнитного момента. Собственный момент импульса ядра — спин ядра — складывается из спинов нуклонов и из орбитальных моментов импульса нуклонов (моментов импульса, обусловленных движением нуклонов внутри ядра). Обе эти величины являются векторами, поэтому спин ядра представляет их векторную сумму. Спин ядра квантуется по закону
где I — спиновое ядерное квантовое число (его часто называют просто спином ядра), которое принимает целые или полуцелые значения 0, Атомное ядро кроме спина обладает магнитным моментом рmя. Магнитный момент ядра связан со спином ядра (см. аналогичное выражение (131.5) для электрона): pmя=gяLя, где g я — коэффициент пропорциональности, называемый ядерным гиромагнитным отношением. Единицей магнитных моментов ядер служит ядерный магнетон
где тp — масса протона (ср. эту формулу с магнетоном Бора (§ 131)). Ядерный магнетон в mp / me»1836 раз меньше магнетона Бора, поэтому магнитные свойства атомов определяются в основном магнитными свойствами его электронов. В случае эффекта Зеемана (см. § 223) при помещении атома в магнитное поле наблюдается расщепление энергетических уровней и спектральных линий (тонкая структура), обусловленное спин-орбитальным взаимодействием электронов. Во внешнем магнитном поле также наблюдается расщепление уровней энергии атома на близко расположенные подуровни (сверхтонкая структура), обусловленное взаимодействием магнитного момента ядра с магнитным полем электронов в атоме. Магнитные моменты ядер могут, таким образом, определяться спектроскопическим методом по сверхтонкой структуре спектральных линий. Однако магнитные моменты ядер примерно на три порядка меньше магнитных моментов электронов (см. (253.1) и (§ 131)), поэтому расщепление спектральных линий, соответствующее сверхтонкой структуре, значительно меньше расщепления за счет взаимодействия между спиновым и орбитальным моментами электрона (тонкая структура). Таким образом, из-за малости эффекта, даже при использовании спектральных приборов очень большой разрешающей способности, точность этого метода невелика. Поэтому были разработаны более точные (не оптические) методы определения магнитных моментов ядер, одним из которых является метод ядерного магнитного резонанса. Явление ядерного магнитного резонанса заключается в следующем: если на вещество, находящееся в сильном постоянном магнитном поле, действовать слабым переменным радиочастотным магнитным полем, то при частотах, соответствующих частотам переходов между ядерными подуровнями, возникает резкий (резонансный) максимум поглощения. Ядерный магнитный резонанс обусловлен происходящими под влиянием переменного магнитного поля квантовыми переходами между ядерными подуровнями. Точность метода задается точностью измерения напряженности постоянного магнитного поля и резонансной частоты, так как по их значениям вычисляются магнитные моменты ядер. Так как для измерения этих величин применяются прецизионные методы, то р mя можно определять с высокой точностью (до шести знаков). Метод ядерного магнитного резонанса позволяет наблюдать ядерный резонанс на ядрах, обладающих магнитным моментом порядка 0,1 m я. Количество вещества, необходимое для измерений, должно составлять 10–3—10 г (в зависимости от значения р mя). Измерение значений магнитных моментов ядер часто сводится к сравнению резонансных частот исследуемых ядер с резонансной частотой протонов, что позволяет освободиться от точной калибровки магнитного поля, которая является довольно трудоемкой. Билет 44 Дефект массы и энергия связи ядра Исследования показывают, что атомные ядра являются устойчивыми образованиями. Это означает, что в ядре между нуклонами существует определенная связь. Массу ядер очень точно можно определить с помощью масс-спектрометров — измерительных приборов, разделяющих с помощью электрических и магнитных полей пучки заряженных частиц (обычно ионов) с разными удельными зарядами Q/m. Масс-спектрометрические измерения показали, что масса ядра меньше, чем сумма масс составляющих его нуклонов. Но так как всякому изменению массы (см. § 40) должно соответствовать изменение энергии, то, следовательно, при образовании ядра должна выделяться определенная энергия. Из закона сохранения энергии вытекает и обратное: для разделения ядра на составные части необходимо затратить такое же количество энергии, которое выделяется при его образовании. Энергия, которую необходимо затратить, чтобы расщепить ядро на отдельные нуклоны, называется энергией связи ядра (см. § 40). Согласно выражению (40.9), энергия связи нуклонов в ядре
где тp, тn, т я — соответственно массы протона, нейтрона и ядра. В таблицах обычно приводятся не массы т я ядер, а массы т атомов. Поэтому для энергии связи ядра пользуются формулой
где m H— масса атома водорода. Так как m H больше mp на величину me, то первый член в квадратных скобках включает в себя массу Z электронов. Но так как масса атома т отличается от массы ядра т я как раз на массу Z электронов, то вычисления по формулам (252.1) и (252.2) приводят к одинаковым результатам. Величина
называется дефектом массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них атомного ядра. Часто вместо энергии связи рассматривают удельную энергию связи dE св — энергию связи, отнесенную к одному нуклону. Она характеризует устойчивость (прочность) атомных ядер, т. е. чем больше dE св, тем устойчивее ядро. Удельная энергия связи зависит от массового числа А элемента (рис. 342). Для легких ядер (А £12) удельная энергия связи круто возрастает до 6¸7 МэВ, претерпевая целый ряд скачков (например, для Уменьшение удельной энергии связи при переходе к тяжелым элементам объясняется тем, что с возрастанием числа протонов в ядре увеличивается и энергия их кулоновского отталкивания. Поэтому связь между нуклонами становится менее сильной, а сами ядра менее прочными. Наиболее устойчивыми оказываются так называемые магические ядра, у которых число протонов или число нейтронов равно одному из магических чисел: 2, 8, 20, 28, 50, 82, 126. Особенно стабильны дваждымагические ядра, у которых магическими являются и число протонов, и число нейтронов (этих ядер насчитывается всего пять: Из рис. 342 следует, что наиболее устойчивыми с энергетической точки зрения являются ядра средней части таблицы Менделеева. Тяжелые и легкие ядра менее устойчивы. Это означает, что энергетически выгодны следующие процессы: 1) деление тяжелых ядер на более легкие; 2) слияние легких ядер друг с другом в более тяжелые. При обоих процессах выделяется огромное количество энергии; эти процессы в настоящее время осуществлены практически: реакции деления и термоядерные реакции.
Билет 45 Ядерные силы. Модели ядра Между составляющими ядро нуклонами действуют особые, специфические для ядра силы, значительно превышающие кулоновские силы отталкивания между протонами. Они называются ядерными силами. С помощью экспериментальных данных по рассеянию нуклонов на ядрах, ядерным превращениям и т.д. доказано, что ядерные силы намного превышают гравитационные, электрические и магнитные взаимодействия и не сводятся к ним. Ядерные силы относятся к классу так называемых сильных взаимодействий. Перечислим основные свойства ядерных сил: 1) ядерные силы являются силами притяжения; 2) ядерные силы являются короткодействующими — их действие проявляется только на расстояниях примерно 10–15 м. При увеличении расстояния между нуклонами ядерные силы быстро уменьшаются до нуля, а при расстояниях, меньших их радиуса действия, оказываются примерно в 100 раз больше кулоновских сил, действующих между протонами на том же расстоянии; 3) ядерным силам свойственна зарядовая независимость: ядерные силы, действующие между двумя протонами, или двумя нейтронами, или, наконец, между протоном и нейтроном, одинаковы по величине. Отсюда следует, что ядерные силыимеютнеэлектрическую природу; 4) ядерным силам свойственно насыщение, т. е. каждый нуклон в ядре взаимодействует только с ограниченным числом ближайших к нему нуклонов. Насыщение проявляется в том, что удельная энергия связи нуклонов в ядре (если не учитывать легкие ядра) при увеличении числа нуклонов не растет, а остается приблизительно постоянной; 5) ядерные силы зависят от взаимной ориентации спинов взаимодействующих нуклонов. Например, протон и нейтрон образуют дейтрон (ядро изотопа 6) ядерные силы не являются центральными, т. е. действующими по линии, соединяющей центры взаимодействующих нуклонов. Сложный характер ядерных сил и трудность точного решения уравнений движения всех нуклонов ядра (ядро с массовым числом А представляет собой систему из А тел) не позволили до настоящего времени разработать единую последовательную теорию атомного ядра. Поэтому на данной стадии прибегают к рассмотрению приближенных ядерных моделей, в которых ядро заменяется некоторой модельной системой, довольно хорошо описывающей только определенные свойства ядра и допускающей более или менее простую математическую трактовку. Из большого числа моделей, каждая из которых обязательно использует подобранные произвольные параметры, согласующиеся с экспериментом, рассмотрим две: капельную и оболочечную. 1. Капельная модель ядра (1936; Н. Бор и Я. И. Френкель). Капельная модель ядра является первой моделью. Она основана на аналогии между поведением нуклонов в ядре и поведением молекул в капле жидкости. Так, в обоих случаях силы, действующие между составными частицами — молекулами в жидкости и нуклонами в ядре, — являются короткодействующими и им свойственно насыщение. Для капли жидкости при данных внешних условиях характерна постоянная плотность ее вещества. Ядра же характеризуются практически постоянной удельной энергией связи и постоянной плотностью, не зависящей от числа нуклонов в ядре. Наконец, объем капли, так же как и объем ядра (см. (251.1)), пропорционален числу частиц. Существенное отличие ядра от капли жидкости в этой модели заключается в том, что она трактует ядрокаккаплю электрически заряженной несжимаемой жидкости (с плотностью, равной ядерной), подчиняющуюся законам квантовой механики. Капельная модель ядра позволила получить полуэмпирическую формулу для энергии связи нуклонов в ядре, объяснила механизм ядерных реакций и особенно реакции деления ядер. Однако эта модель не смогла, например, объяснить повышенную устойчивость ядер, содержащих магические числа протонов и нейтронов. 2. Оболочечная модель ядра (1949—1950; американский физик М. Гепперт-Майер (1906—1975) и немецкий физик X.Иенсен (1907—1973)). Оболочечная модель предполагает распределение нуклонов в ядре по дискретным энергетическим уровням (оболочкам), заполняемым нуклонами согласно принципу Паули, и связывает устойчивость ядер с заполнением этих уровней. Считается, что ядра с полностью заполненными оболочками являются наиболее устойчивыми. Такие особо устойчивые (магические) ядра действительно существуют (см. § 252). Оболочечная модель ядра позволила объяснить спины и магнитные моменты ядер, различную устойчивость атомных ядер, а также периодичность изменений их свойств. Эта модель особенно хорошо применима для описания легких и средних ядер, а также для ядер, находящихся в основном (невозбужденном) состоянии. По мере дальнейшего накопления экспериментальных данных о свойствах атомных ядер появлялисьвсе новые факты, не укладывающиеся в рамки описанных моделей. Так возникли обобщенная модель ядра (синтез капельной и оболочечной моделей), оптическая модель ядра (объясняет взаимодействие ядер с налетающими частицами) и другие модели.
Билет 46 Радиоактивное излучение и его виды Французский физик А. Беккерель (1852—1908) в 1896 г. при изучении люминесценции солей урана случайно обнаружил самопроизвольное испускание ими излучения неизвестной природы, которое действовало на фотопластинку, ионизировало воздух, проникало сквозь тонкие металлические пластинки, вызывало люминесценцию ряда веществ. Продолжая исследование этого явления, супруги Кюри — Мария (1867—1934) и Пьер — обнаружили, что беккерелевское излучение свойственно не только урану, но и многим другим тяжелым элементам, таким, как торий и актиний. Они показали также, что урановая смоляная обманка (руда, из которой добывается металлический уран) испускает излучение, интенсивность которого во много раз превышает интенсивность излучения урана. Таким образом удалось выделить два новых элемента — носителя беккерелевского излучения: полоний Обнаруженное излучение было названо радиоактивным излучением, а само явление — испускание радиоактивного излучения — радиоактивностью. Дальнейшие опыты показали, что на характер радиоактивного излучения препарата не оказывают влияния вид химического соединения, агрегатное состояние, механическое давление, температура, электрические и магнитные поля, т. е. все те воздействия, которые могли бы привести к изменению состояния электронной оболочки атома. Следовательно, радиоактивные свойства элемента обусловлены лишь структурой его ядра. В настоящее время под радиоактивностью понимают способность некоторых атомных ядер самопроизвольно (спонтанно) превращаться в другие ядра с испусканием различных видов радиоактивных излучений и элементарных частиц. Радиоактивность подразделяется на естественную (наблюдается у неустойчивых изотопов, существующих в природе) и искусственную (наблюдается у
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.143 (0.015 с.) |

 , (169)
, (169) (170)
(170) , поэтому
, поэтому  .
.
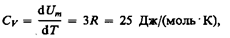 (73.1)
(73.1)
 . Фонон есть квант энергии звуковой волны (так как упругие волны — волны звуковые). Фононы являются квазичастицами — элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах.
. Фонон есть квант энергии звуковой волны (так как упругие волны — волны звуковые). Фононы являются квазичастицами — элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах. , где
, где 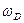 —предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел (см. § 73 и рис. 113).
—предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел (см. § 73 и рис. 113). , гдеХ — символхимического элемента, Z атомный номер (число протонов в ядре), А — массовоечисло (число нуклонов в ядре).
, гдеХ — символхимического элемента, Z атомный номер (число протонов в ядре), А — массовоечисло (число нуклонов в ядре). Н—протий (Z =1, N =0),
Н—протий (Z =1, N =0),  Н—дейтерий (Z =1, N =1),
Н—дейтерий (Z =1, N =1),  Н — тритий (Z =1, N =2), олово—десять, и т. д. В подавляющем большинстве случаев изотопы одного и того же химического элемента обладают одинаковыми химическими и почти одинаковыми физическими свойствами (исключение составляют, например, изотопы водорода), определяющимися в основном структурой электронных оболочек, которая является одинаковой для всех изотопов данного элемента. Примером ядер-изобар могут служить ядра
Н — тритий (Z =1, N =2), олово—десять, и т. д. В подавляющем большинстве случаев изотопы одного и того же химического элемента обладают одинаковыми химическими и почти одинаковыми физическими свойствами (исключение составляют, например, изотопы водорода), определяющимися в основном структурой электронных оболочек, которая является одинаковой для всех изотопов данного элемента. Примером ядер-изобар могут служить ядра  Ве,
Ве,  В,
В,  С. В настоящее время известно более 2500 ядер, отличающихся либо Z, либо А, либо тем и другим.
С. В настоящее время известно более 2500 ядер, отличающихся либо Z, либо А, либо тем и другим.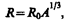 (251.1)
(251.1)
 , 1,
, 1,  ,.... Ядра с четными А имеют целые I, с нечетными — полуцелые I.
,.... Ядра с четными А имеют целые I, с нечетными — полуцелые I. (253.1)
(253.1)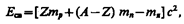 (252.1)
(252.1)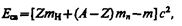 (252.2)
(252.2)
 He — 7,1 МэВ, для
He — 7,1 МэВ, для  Li — 5,3 МэВ), затем более медленно возрастает до максимальной величины 8,7 МэВ у элементов с А =50¸60, а потом постепенно уменьшается у тяжелых элементов (например, для
Li — 5,3 МэВ), затем более медленно возрастает до максимальной величины 8,7 МэВ у элементов с А =50¸60, а потом постепенно уменьшается у тяжелых элементов (например, для  U она составляет 7,6 МэВ). Отметим для сравнения, что энергия связи валентных электронов в атомах составляет примерно 10 эВ (в 106! раз меньше).
U она составляет 7,6 МэВ). Отметим для сравнения, что энергия связи валентных электронов в атомах составляет примерно 10 эВ (в 106! раз меньше).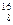 O,
O, 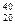 Ca,
Ca,  Ca,
Ca,  Pb).
Pb). Рo и радий
Рo и радий  Ra.
Ra.


