
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение моментов. Результирующий момент многоэлектронной системы.Содержание книги
Поиск на нашем сайте
КВАНТОВОЕ СЛОЖЕНИЕ МОМЕНТОВ - сложение моментов (орбитальных, спиновых, полных) независимых частиц (или систем - атомов, молекул и т. д.) по законам квантовой механики. Применяется также назв. векторное сложение моментов. В случае двух частиц задача состоит в определении спектра возможных собств. значений оператора квадрата суммарного момента J=j 1+ j 2 +...+j N(4) может быть выполнено последоват. применением операции (1). В частности, наиб. значение J=j 1+ j 2 +...+j N имеет кратность, равную единице (т. е. встречается в разложении прямого произведения
Каждый электрон в атоме обладает орбитальным моментом импульса и собственным моментом Механические моменты связаны с соответствующими магнитными моментами, вследствие чего между всеми имеется взаимодействие. Моменты складываются в результирующий момент атома При этом возможны два случая. 1. Моменты взаимодействуют между собой сильнее, чем с которые в свою очередь сильнее связаны друг с другом, чем с Вследствие этого все складываются в результирующую моменты складываются в а затем уже дают суммарный момент атома Такой вид связи встречается чаще всего и называется связью Рёссель — Саундерса или вязью. 2. Каждая пара взаимодействует между собой сильнее, чем с другими вследствие чего образуются результирующие для каждого электрона в отдельности, которые затем уже объединяются в атома. Такой вид связи, называемый вязью, наблюдается у тяжелых атомов. Сложение моментов осуществляется по квантовым законам (см. § 24). Рассмотрим подробнее сложение моментов в случае связи Рёссель — Саундерса. Орбитальные квантовые числа U всегда бывают целыми. Соответственно квантовое число L суммарного орбитального момента также бывает целым (либо нулем). Квантовое число S результирующего спинового момента атома может быть целым или полуцелым в зависимости от того, каким является число электронов в атоме — четным или нечетным. При четном числе электронов N квантовое число S принимает все целые значения от «параллельны» друг другу) до нуля (все попарно компенсируют друг друга). Так, например, при может иметь значения 2, 1, 0. При нечетном N квантовое число S принимает все полуцелые значения от «параллельны» друг другу) до кроме одного, попарно компенсируют друг друга). Например, при возможными значениями S будут: При данных квантовое число J результирующего, момента может иметь одно из следующих значений:
Следовательно, будет целым, если S — целое (т. е. при четном числе электронов в атоме), и полуцелым, если S — полуцелое (т. е. при нечетном числе электронов). Так, например, 1) в случае возможные значения J равны 3, 2, 1; 2) в случае возможные значения равны Энергия атома зависит от взаимной ориентации моментов (т. е. от квантового числа L), от взаимной ориентации моментов (от квантового числа S) и от взаимной ориентации квантового числа l). Условно терм атома записывается следующим образом:
где под L подразумевается одна из букв S, Р, D, F и т. д. в зависимости от значения числа L. Например, термы
относятся к состояниям с одинаковыми одинаковыми но различными J, равными 0, 1, 2. Символ (32.1) содержит в себе сведения о значениях трех квантовых чисел L, S и. В случае, когда, стоящее слева вверху число дает мультиплетность терма, т. е. количество подуровней, отличающихся значением числа J (см. (32.2)). В случае, когда фактическая мультиплетность равна Однако символ терма все равно пишут в виде (32.1), иначе он не содержал бы сведений о значении квантового числа Обозначениями типа (32.1) мы уже пользовались в § 29 применительно к атомам щелочных металлов. Однако для этих элементов характерно то, что S атома, совпадая с s валентного электрона, равно Теперь же мы познакомились с символическими обозначениями термов для любых случаев.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.68 (0.007 с.) |

 и его проекции
и его проекции  на фиксированную ось и соответствующих собств. ф-ций
на фиксированную ось и соответствующих собств. ф-ций  - операторы моментов частиц 1,2). Спектр имеет вид
- операторы моментов частиц 1,2). Спектр имеет вид 
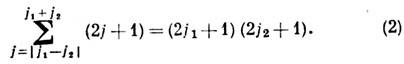
 группы вращений трёхмерного пространства SO(3) на неприводимые компоненты, что символически записывается в виде
группы вращений трёхмерного пространства SO(3) на неприводимые компоненты, что символически записывается в виде 
 только один раз). В теории атомов применяются след. схемы сложения моментов: 1) связь Расселла - Саундерса (LS- связъ),в к-рой сначала складываются орбитальные и спиновые моменты отд. электронов:
только один раз). В теории атомов применяются след. схемы сложения моментов: 1) связь Расселла - Саундерса (LS- связъ),в к-рой сначала складываются орбитальные и спиновые моменты отд. электронов:






