
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренняя энергия и способы её изменения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Энергия, которая связана со всевозможными движениями частиц и их взаимодействием, энергию покой частиц называют внутренней. Внутреннюю энергию макроскопической системы можно представить как сумму кинетических энергий теплового движения молекул (поступ, вращ, кин эн атомов), потенциальных энергий взаимодействий молекул между собой, потенциальную энергию вз атомов в многоатом мол и кристаллах и внутренних энергий атомов. Внутренняя энергия явл функцией состояния системы.ЕWki Wпi Wпai Ui, чаще всго изучаются процессы при которых u=конст, и её отбрасывают.,В модели идеального газа также отбрасывают пот эн вз, т.к. вз на расстоянии не учит., для одноат идел газа Wпаi=0, U=EWki U=NWc, где Wc средняя энергия молекул, а N=m/M Na, при учёте степеней свободы и i/2m/M RT.,для ВДВ U=m/Mc_vT-m^2/M^2 a/V Изменяется за счёт мех энергии при соверш раб над телом. За счёт внутр энергии других тел при теплообмене. Теплопередача за счёт теплопроводности, конвекции, электромагнитного излучения. Первый закон тд. При изменении внутренней энергии системы за счёт внутренней энергии других тел (притеплообмене, за счет мех эн др тел, изменение внутренней энергии системы dU равно сумме количества теплоты, сообщённого системе dQ и работы dA’ над системой. ΔU=Q+A’ (A=-A’) Q=delta U+A при изох проц Cv=dQv/dt=dU/dt, отношение Cv/Cp=гамма=i+2/i –показатель адиабаты. Количество теплоты и теплоёмкость. Q- энергия, переданная системе при теплообмене. C=dQ/dt, Суд= C/m, Q=mCуд(T2-T1) C-молярн=MC/m, Q идёт не только на нагревание но и на соверщ работы. Теплоёмкость ид газов при пост объёме cv= im/2MR cv=Cv*M/m Работа газа dA=pdV – при изм обьёма A=int(V1-V2)(pdV) Коли́чество теплоты́ — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основныхтермодинамических величин. Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние. Рассмотрим систему, состоящую из двух тел
где
где
Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела Отметим, что, как и совершённая работа, количество переданной теплоты зависит от конкретного процесса, совершённого над телом. Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:
Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объеме равна: Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии длятермодинамических систем. Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физикаДж. П. Джоуля и немецкого физика Г. Гельмгольца[1]. Согласно первому началу термодинамики, термодинамическая система может совершать работутолько за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника. уществует несколько эквивалентных формулировок первого начала термодинамики В любой изолированной системе запас энергии остаётся постоянным.[2] Это — формулировка Дж. П. Джоуля (1842 г.). Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.
Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты
Для элементарного количества теплоты
Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил. Важно заметить, что Квантовая теория теплоёмкостей Эйнштейна была создана Эйнштейном в 1907 году при попытке объяснить экспериментально наблюдаемую зависимость теплоёмкости от температуры. При разработке теории Эйнштейн опирался на следующие предположения: § Атомы в кристаллической решетке ведут себя как гармонические осцилляторы, не взаимодействующие друг с другом. § Частота колебаний всех осцилляторов одинакова. § Число осцилляторов в 1 моле вещества равно § Энергия их квантована: § Число осцилляторов с различной энергией определяется распределением Больцмана: Внутренняя энергия 1 моля вещества:
и составляет:
отсюда:
Определяя теплоёмкость как производную внутренней энергии по температуре, получаем окончательную формулу для теплоёмкости:
Согласно модели, предложенной Эйнштейном, при абсолютном нуле температуры теплоёмкость стремится к нулю, при больших температурах, напротив, выполняется закон Дюлонга — Пти. Величина
4.11 Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — термодинамический процесс, происходящий в системе при постоянном внешнем давлении; на термодинамической диаграмме изображается изобарой. Пример изобарного процесса — расширение газа в цилиндре со свободно ходящим нагруженным поршнем. Если изобарный процесс происходит настолько медленно, что давление в системе можно считать постоянным и равным внешнему давлению, а температуpa меняется так медленно, что в каждый момент времени сохраняется термодинамическое равновесие, то изобарный процесс считается обратимым. Для осуществления изобарного процесса к системе надо подводить (или отводить) теплоту ΔQ, которая расходуется на работу расширения PdV и изменение внутренней энергии dU, то есть ΔQ = PdV + dU = TdS, dS — изменение энтропии, T — абсолютная температура. Для идеального газа при изобарном процессе объём пропорционален температуре (закон Гей-Люссака) в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц. Работа, совершаемая при изобарных процессах равна произведению внешнего давления на изменение объёма, а для обратимых изобарных процессов внешнее давление равно внутреннему. Изменение энтропии при обратимом изобарном процессе равно Изохорический или изохорный процесс от др.-греч. ισος — «ровный», и chora —«пространство, занятое место») — это термодинамический процесс, который происходит при постоянстве объёма. В газах и жидкостях осуществляется очень просто: для этого достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. При изохорическом процессе давление идеального газа прямо пропорциально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется, так как часть теплоты, которую получает система, расходуется на увеличение энергии взаимодействия частиц. На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: T (температура), V (объем) и P (давление). Из определения работы следует, что изменение работы при изохорном процессе равна: Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре. Несколько изотерм для идеального газа нa p-V диаграмме Для осуществления И. п. систему обычно помещают в термостат (массивное тело, находящееся в тепловом равновесии), теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро и её температура практически не отличается от температуры термостата. Можно осуществить И. п. иначе — с применением источников или стоков тепла, контролируя постоянство температуры с помощью термометров. К И. п. относится, например, кипение жидкости или плавление твёрдого тела при постоянном давлении. В идеальном газе при И. п. произведение давления на объём постоянно (Бойля — Мариотта закон). При И. п. системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа. Работа, совершенная идеальным газом в И.п., равна В твёрдом теле и большинстве жидкостей И. п. очень мало изменяет объём тела, если только не происходит фазовый переход. Первый закон термодинамики для изотермического процесса записывается в виде:
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством. Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы[3]. Адиабатический процесс для идеального газа описывается уравнением Пуассона. Работа газа Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок
где F — сила, с которой газ действует на поршень. Перепишем уравнение:
где s — площадь поршня. Тогда работа будет равна[9][10]
где Основное уравнение термодинамики примет вид[11]:
Это условие будет выполняться, если скорость хода поршня (протекания процесса в общем случае) будет удовлетворять определённым условиям. С одной стороны она должна быть достаточно малой, чтобы процесс можно было считать квазистатическим. Иначе при резком изменении хода поршня давление, которое его перемещает, будет отличаться от давления в целом по газу. То есть газ должен находиться в равновесии, без турбулентностей и неоднородностей давления и температуры. Для этого достаточно передвигать поршень со скоростью, существенно меньшей, чем скорость звука в данном газе. С другой стороны скорость должна быть достаточно большой, чтобы можно было пренебречь обменом тепла с окружающей средой и процесс оставался адиабатическим[12][13]. Однако работа может совершаться и другими путями — например, идти на преодоление межмолекулярного притяжения газов. В этом случае параллельно с изменением внутренней энергии будет происходить процессы совершения нескольких работ разной физической природы, и основное уравнение термодинамики примет вид:
где
Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:
Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объеме равна:
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.117 (0.008 с.) |

 и
и  . Предположим, что тело
. Предположим, что тело  , где
, где  — изменение внутренней энергии тела
— изменение внутренней энергии тела 
 — макроскопическая работа внешних сил над телом
— макроскопическая работа внешних сил над телом 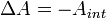
 — работа, совершённая телом
— работа, совершённая телом 
 первое начало становится содержательным законом, допускающим экспериментальную проверку.
первое начало становится содержательным законом, допускающим экспериментальную проверку. Единица измерения теплоёмкости в системе СИ — Дж/К.Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T:
Единица измерения теплоёмкости в системе СИ — Дж/К.Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T: R = 8.31 Дж/(моль К) — универсальная газовая постоянная.А при постоянном давлении
R = 8.31 Дж/(моль К) — универсальная газовая постоянная.А при постоянном давлении 

 , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества
, сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества  при химическом потенциале
при химическом потенциале  , и работы
, и работы  [3], совершённой над системой внешними силами и полями, за вычетом работы
[3], совершённой над системой внешними силами и полями, за вычетом работы  .
.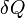 , элементарной работы
, элементарной работы  и малого приращения
и малого приращения 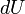 внутренней энергии первый закон термодинамики имеет вид:
внутренней энергии первый закон термодинамики имеет вид: .
.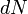 являются полными дифференциалами, а
являются полными дифференциалами, а  , где
, где 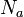 — число Авогадро.
— число Авогадро. ,
, 

 .
. находится из соотношения для среднего значения:
находится из соотношения для среднего значения:
 ,
, .
. .
. иногда называется температурой Эйнштейна.
иногда называется температурой Эйнштейна.
 Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует:
Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует: 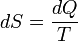 ыше была выведена формула для определения количества теплоты. Перепишем ее в диференциальном виде:
ыше была выведена формула для определения количества теплоты. Перепишем ее в диференциальном виде:  где ν — количество вещества, — молярная теплоемкостью при постоянном объеме.
где ν — количество вещества, — молярная теплоемкостью при постоянном объеме. где — Nчисло частиц газа, —T температура, и —V1V2 и объём газа в начале и конце процесса, —k- Постоянная Больцмана.
где — Nчисло частиц газа, —T температура, и —V1V2 и объём газа в начале и конце процесса, —k- Постоянная Больцмана.

 Серьёзное исследование адиабатических процессов началось в XVIII веке[1].
Серьёзное исследование адиабатических процессов началось в XVIII веке[1]. 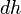 совершать работу[9][10]
совершать работу[9][10]


 — давление газа,
— давление газа,  — малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки
— малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки  на которых расширение одинаково[9].
на которых расширение одинаково[9].

 ,
,  — дифференциальное выражение для работы,
— дифференциальное выражение для работы,  — внешние параметры, которые меняются при совершении работы,
— внешние параметры, которые меняются при совершении работы, 


