
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярно кинетическое строение вещества.Содержание книги
Поиск на нашем сайте
4.1 1) Тепловое излучение Тела, нагретые до достаточно высокой температуры, приобретают способность светиться. По мере уменьшения температуры изменяется не только интенсивность излучения но и его спектральный состав. В нём всё сильнее обнаруживается преобладание длинных волн – красных и инфракрасных. Электромагнитное излучение, возникающее за счёт внутренней энергии излучающего тела и зависящее только от температуры называется тепловым излучением. Если энергия расходуемая на излучение не восполняется теплом, то излучение с течением времени уменьшается и температура постепенно понижается. Единственное излучение, способное находиться в равновесии с веществом. Равновесное излучение. Устанавливается в адиабатно - замкнутой теплоизолированной системе (теплоизолированной) 2) Законы Кирхгофа (или правила Кирхгофа) — неизменные соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров. В этом случае законы формулируются следующим образом. Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком). Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве, то она описывается уравнениями напряжений. Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Зависимость испускательной способности от частоты и температуры называется функцией Киргофа: rv = f(f,T). 3) Абсолютно чёрное тело — физическая абстракция, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой. Первый закон излучения Вина В 1893 году Вильгельм Вин, исходя из представлений классической термодинамики, вывел следующую формулу:
Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина. Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана-Больцмана, но нельзя найти значения постоянных, входящих в эти законы. Исторически именно первый закон Вина назывался законом смещения, но в настоящее время термином "закон смещения Вина" называют закон максимума. Второй закон излучения Вина.В 1896 году Вин на основе дополнительных предположений вывел второй закон:
Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина. Попытка описать излучение абсолютно чёрного тела исходя из классических принципов термодинамики и электродинамики приводит к закону Рэлея — Джинса: Закон Планка Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка: 4.2 1)Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект. Законы фотоэффекта:
Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности. 3-ий закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода, покидает металл: 2) Экспериментальное изучение фотоэффекта
Катод через кварцевое стекло освещается светом. Под действием света из катода вырываются электроны (называемые фотоэлектронами), которые летят к аноду (положительно заряженному электроду) и образуют фототок, регистрируемый миллиамперметром С помощью такой установки, используя электроды, изготовленные из разных материалов, снимались вольт-амперные характеристики (ВАХ) при различных значениях падающего светового потока Ф. ВАХ - зависимость силы фототока I от напряжения U между электродами (анодом и катодом). Вид такой зависимости представлен на рисунке 4. Из вольт-амперной характеристики видно, что:
Ток насыщения соответствует тому состоянию, когда все фотоэлектроны, покидающие материал за 1 с, достигают анода. Работа задерживающего электрического поля определяется максимальной кинетической энергией фотоэлектронов: q·U = m·V2max/2 3) Уравнение Эйнштейна А. Эйнштейн показал, что все закономерности фотоэффекта объясняются, если предположить, что свет поглощается такими же порциями (квантами, фотонами), какими он по гипотезе Планка испускается. Согласно Эйнштейну, энергия фотона E=hν, полученная электроном, усваивается им целиком. Рассмотрим с квантовой точки зрения фотоэффект в металлах. Электрон удерживается в металле притяжением положительных ионов кристаллической решетки. Для того, чтобы покинуть металл, электрон должен совершить работу выхода Aвых. Если полученная электроном энергия E = hν > Aвых, то он при вылете будет обладать кинетической энергией. Величина этой энергии максимальна, если электрон покидает металл с поверхности, а не с какой-то глубины. В этом случае в соответствии с законом сохранения энергии выполняется соотношение, которое называется уравнением Эйнштейна для внешнего фотоэффекта: E = hν = Aвых +W max. Из формулы Эйнштейна видно, что фотоэффект с поверхности данного вещества наблюдается только при частотах, удовлетворяющих условию hν ≥ Aвых. Тогда красную границу фотоэффекта (ν0 или λ0) можно определить из уравнения hν0 = Aвых, т.е. Из формул (2.12) и (2.13) следует, что U3 является линейной функцией частоты ν падающего света (рис. 28): Точка пересечения U f(ν) 3. = с осью абсцисс (U3 0 =) дает значение красной границы фотоэффекта ν0. Экстраполируя прямую до пересечения с осью ординат, можно определить Aвых для данного металла. На основе фотоэффекта работают фотоэлементы — приемники излучения, которые преобразуют энергию излучения в электрическую. Они используются в различных системах автоматизации, сигнализации, связи и т.д. Кремневые фотоэлементы применяются для создания солнечных батарей.
4.3 1) Фото́н (от др.-греч. φῶς, род. пад. φωτός, «свет») — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Заряд фотона также равен нулю. Фотон может находиться только в двух спиновых состояниях с проекцией спина на направление движения (спиральностью) ±1. Этому свойству в классической электродинамике соответствует круговая правая и левая поляризация электромагнитной волны. Фотону как элементарной частице свойственен корпускулярно-волновой дуализм, он проявляет одновременно свойства частицы и волны. Фотоны обозначаются буквой, поэтому их часто называют гамма-квантами (особенно фотоны высоких энергий); эти термины практически синонимичны. С точки зрения Стандартной модели фотон является калибровочным бозоном. Виртуальные фотоны являются переносчиками электромагнитного взаимодействия, таким образом обеспечивая взаимодействие, например, между двумя электрическими зарядами.[2] 2) Корпускулярно-волновой дуализм — теория в квантовой механике, гласящая, что в зависимости от системы отсчета поток электромагнитного излучения можно рассматривать и как поток частиц (корпускул), и как волну. В частности, свет — это и корпускулы (фотоны), и электромагнитные волны. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла.[1]. Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может[источник не указан 26 дней] быть разделён на несколько пучков оптическими делителями лучей. Корпускулярные свойства света проявляются при фотоэффекте. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон). 4.4 1) 2) Теория Бора позволила объяснить существование линейчатых спектров.
4.7 4.8 Термодинамические параметры Параметры состояния Термодинамические параметры - температура, плотность, давление, объем, удельное электрическое сопротивление и другие физические величины: Основное уравнение МКТ. Уравнение, выражающее связь давления идеального газа со средними значениями характеристик молекул, называется осн ур МКТ. Вводится давление (мех напр) p=dF_д/dS, -модуль нормальной силы, действующей на участок поверхности, при равном распределении: p=Fд/S, давление на стенки сосуда по 2 з-ну Ньютона Fд=delta p_x/delta t, p=delta p_x/(S*delta t) –давление равно импульсу передаваемому молекулами газа единице площади поверхности сосуда за единицу времени. Изменение импульса при ударе о стенку: delta p_x=m_M*v_x-(-m_M*v_x)=2m_M*v_x, если молекула летит под углом к стенке то изменение импульса по оси у =0, давление Fy=0.Ударения молекул о стенки будут проходить через промежуток времени delta t, необходимого для того, чтобы молекуле пересечь сосуд и вернуться обратно 2l. Delta t=2l/v_x. Средняя сила Fi=delta p_xi/delta t=1m_M*v_xi^2/2l=m_M*v_xi^2/l, сила со стороны всех молекул: F=summ(Fi)=(m_M/l)*summ(i)(v_xi^2) среднее значение квадрата х составляющей скорости: v_xc^2=1/Nsumm(v_xi^2), F=..., квадрат любой скорости равен сумме квадратов проекций, для v_k^2=v_...c^2, так как молеклы движутся хаотически, все эти проекции равны. И v_xc^2=1/3v_k^2, подставим в F=..., тогда p=F/S=..., получим основное уравнение динамики, выражающее давление идеального газа через концентрацию и среднюю квадратичную скорость молекул p=1/3nm_Mv_k^2, p пропорц n, p m_M, p v_k^2, можно записать в виде p=2/3nWk.c.п. – средняя скорость поступательного движения молекул.
Вну́тренняя эне́ргия идеального газа Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме,
Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:
где
Термодинамическая вероятность — число способов, которыми может быть реализовано состояние физической системы. В термодинамике состояние физической системы характеризуется определёнными значениями плотности, давления, температуры и др. измеримых величин. Перечисленные величины определяют состояние системы в целом (её макросостояние). Однако при одной и той же плотности, температуре и т. д. частицы системы могут различными способами распределиться в пространстве и иметь различные импульсы. Каждое данное распределение частиц называется микросостоянием системы. Вероятность термодинамическая (обозначается W) равна числу микросостояний, реализующих данное макросостояние, из чего следует, что Вероятность термодинамическая не является вероятностью в математическом смысле. Она применяется в статистической физике для определения свойств систем, находящихся в термодинамическом равновесии (для них Вероятность термодинамическая имеет максимальное значение). Для расчёта Вероятность термодинамическая существенно, считаются ли частицы системы различимыми или неразличимыми. Поэтому классическая и квантовая механика приводят к разным выражениям для Вероятность термодинамическая 4.9 Уравнение состояния.f(p,V,T) – функциональная зависимость, которая называется термическим уравнением состояния тела. Примерами являются Ур-ния Менделеева-Клапейрона и В-д-В. На основе опытных законов Бойля-Мариотта, Гей-Люссака и Шарля, описывающих соответственно изотермический, изобарный и изохорный процессы изменения состояния идеальных газов, было получено уравнение состояния. Ур-ние Менделеева-Клайперона
Ур-ние Вдв. Для реальных газов уравнения менд-к. выпоняется до тех пор, пока давление не слишком высоко. При высоком давлении обьём газа меньше, соответствующего объёма идеального газа. Для реального газа оказывается недоступным объём, из-за других молекул (V-delta V) delta V=(m/M)b, где b-поправка на недост V в расчёте на 1 моль газа. B=4NaV_M, с учётом введённой поправки, уравнение состояния газа примет вид (Ур сост Клаузиуса0 p(v-(m/M)b)=(m/M)RT давление с учётом поправки delta p + p, тогда: (p+(m^2*a)/(M^2/V^2))V=m/MRT, где а – постоянная, характерная для газа. (p+(m^2*a)/(M^2/V^2))*(v-(m/M)b)= m/MRT –ур-ние Ван-дер-Ваальса. Изотермы реального газа и ВДВ Получаем Ур-ние умножив ВДВ на V^2 и раскрыв скобки – описвающее поведение газов –изотермы. Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре. Несколько изотерм для идеального газа нa p-V диаграмме Для осуществления И. п. систему обычно помещают в термостат (массивное тело, находящееся в тепловом равновесии), теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро и её температура практически не отличается от температуры термостата. Можно осуществить И. п. иначе — с применением источников или стоков тепла, контролируя постоянство температуры с помощью термометров. К И. п. относится, например, кипение жидкости или плавление твёрдого тела при постоянном давлении. В идеальном газе при И. п. произведение давления на объём постоянно (Бойля — Мариотта закон). При И. п. системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа. Работа, совершенная идеальным газом в И.п., равна В твёрдом теле и большинстве жидкостей И. п. очень мало изменяет объём тела, если только не происходит фазовый переход. Первый закон термодинамики для изотермического процесса записывается в виде:
4.10 4.11 Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — термодинамический процесс, происходящий в системе при постоянном внешнем давлении; на термодинамической диаграмме изображается изобарой. Пример изобарного процесса — расширение газа в цилиндре со свободно ходящим нагруженным поршнем. Если изобарный процесс происходит настолько медленно, что давление в системе можно считать постоянным и равным внешнему давлению, а температуpa меняется так медленно, что в каждый момент времени сохраняется термодинамическое равновесие, то изобарный процесс считается обратимым. Для осуществления изобарного процесса к системе надо подводить (или отводить) теплоту ΔQ, которая расходуется на работу расширения PdV и изменение внутренней энергии dU, то есть ΔQ = PdV + dU = TdS, dS — изменение энтропии, T — абсолютная температура. Для идеального газа при изобарном процессе объём пропорционален температуре (закон Гей-Люссака) в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц. Работа, совершаемая при изобарных процессах равна произведению внешнего давления на изменение объёма, а для обратимых изобарных процессов внешнее давление равно внутреннему. Изменение энтропии при обратимом изобарном процессе равно Изохорический или изохорный процесс от др.-греч. ισος — «ровный», и chora —«пространство, занятое место») — это термодинамический процесс, который происходит при постоянстве объёма. В газах и жидкостях осуществляется очень просто: для этого достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. При изохорическом процессе давление идеального газа прямо пропорциально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется, так как часть теплоты, которую получает система, расходуется на увеличение энергии взаимодействия частиц. На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: T (температура), V (объем) и P (давление). Из определения работы следует, что изменение работы при изохорном процессе равна: Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре. Несколько изотерм для идеального газа нa p-V диаграмме Для осуществления И. п. систему обычно помещают в термостат (массивное тело, находящееся в тепловом равновесии), теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро и её температура практически не отличается от температуры термостата. Можно осуществить И. п. иначе — с применением источников или стоков тепла, контролируя постоянство температуры с помощью термометров. К И. п. относится, например, кипение жидкости или плавление твёрдого тела при постоянном давлении. В идеальном газе при И. п. произведение давления на объём постоянно (Бойля — Мариотта закон). При И. п. системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа. Работа, совершенная идеальным газом в И.п., равна В твёрдом теле и большинстве жидкостей И. п. очень мало изменяет объём тела, если только не происходит фазовый переход. Первый закон термодинамики для изотермического процесса записывается в виде:
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством. Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы[3]. Адиабатический процесс для идеального газа описывается уравнением Пуассона. Работа газа Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок
где F — сила, с которой газ действует на поршень. Перепишем уравнение:
где s — площадь поршня. Тогда работа будет равна[9][10]
где Основное уравнение термодинамики примет вид[11]:
Это условие будет выполняться, если скорость хода поршня (протекания процесса в общем случае) будет удовлетворять определённым условиям. С одной стороны она должна быть достаточно малой, чтобы процесс можно было считать квазистатическим. Иначе при резком изменении хода поршня давление, которое его перемещает, будет отличаться от давления в целом по газу. То есть газ должен находиться в равновесии, без турбулентностей и неоднородностей давления и температуры. Для этого достаточно передвигать поршень со скоростью, существенно меньшей, чем скорость звука в данном газе. С другой стороны скорость должна быть достаточно большой, чтобы можно было пренебречь обменом тепла с окружающей средой и процесс оставался адиабатическим[12][13]. Однако работа может совершаться и другими путями — например, идти на преодоление межмолекулярного притяжения газов. В этом случае параллельно с изменением внутренней энергии будет происходить процессы совершения нескольких работ разной физической природы, и основное уравнение термодинамики примет вид:
где
Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:
Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объеме равна:
4.12 Цикл Карно.
Термодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия) совпадают.Идеализированные термодинамические циклы являются приближениями процессов, происходящих в реальных тепловых машинах для превращения тепловой энергии (то есть, внутренней энергии) в механическую работу, а также для охлаждения (при использовании обратного цикла).Тепловая машина состоит из рабочего тела, которое и проходит цикл, нагревателя и холодильника (с помощью которых меняется состояние рабочего тела).Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропия системы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, состоящей только из рабочего тела, нагревателя и холодильника, является Цикл Карно. Существуют также циклы Стирлинга и Эрикссона, в которых обратимость достигается путём введения дополнительного прибора — регенератора. Можно показать (см. статью Цикл Карно), что обратимые циклы обладают наибольшей эффективностью. 4.13 4.1 1) Тепловое излучение Тела, нагретые до достаточно высокой температуры, приобретают способность светиться. По мере уменьшения температуры изменяется не только интенсивность излучения но и его спектральный состав. В нём всё сильнее обнаруживается преобладание длинных волн – красных и инфракрасных. Электромагнитное излучение, возникающее за счёт внутренней энергии излучающего тела и зависящее только от температуры называется тепловым излучением. Если энергия расходуемая на излучение не восполняется теплом, то излучение с течением времени уменьшается и температура постепенно понижается. Единственное излучение, способное находиться в равновесии с веществом. Равновесное излучение. Устанавливается в адиабатно - замкнутой теплоизолированной системе (теплоизолированной) 2) Законы Кирхгофа (или правила Кирхгофа) — неизменные соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров. В этом случае законы формулируются следующим образом. Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.134 (0.017 с.) |

 .где uν — плотность энергии излучения ν — частота излучения T — температура излучающего тела f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.
.где uν — плотность энергии излучения ν — частота излучения T — температура излучающего тела f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.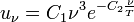 где uν — плотность энергии излученияν — частота излученияT — температура излучающего телаC1,C2 — константы.
где uν — плотность энергии излученияν — частота излученияT — температура излучающего телаC1,C2 — константы. Эта формула предполагает квадратичное возрастание спектральной плотности излучения в зависимости от его частоты. На практике такой закон означал бы невозможность термодинамического равновесия между веществом и излучением, поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию излучения коротковолновой области спектра. Такое гипотетическое явление было названо ультрафиолетовой катастрофой.
Эта формула предполагает квадратичное возрастание спектральной плотности излучения в зависимости от его частоты. На практике такой закон означал бы невозможность термодинамического равновесия между веществом и излучением, поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию излучения коротковолновой области спектра. Такое гипотетическое явление было названо ультрафиолетовой катастрофой. где I(ν)dν — мощность излучения на единицу площади излучающей поверхности в диапазоне частот от ν до ν + dν.
где I(ν)dν — мощность излучения на единицу площади излучающей поверхности в диапазоне частот от ν до ν + dν.  где u(λ)dλ — мощность излучения на единицу площади излучающей поверхности в диапазоне длин волн от λ до λ + dλ.
где u(λ)dλ — мощность излучения на единицу площади излучающей поверхности в диапазоне длин волн от λ до λ + dλ. (или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и если
(или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и если  , то фотоэффект уже не происходит.
, то фотоэффект уже не происходит.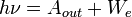 , где
, где 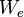 — максимальная кинетическая энергия, которую может иметь электрон при вылете из металла.
— максимальная кинетическая энергия, которую может иметь электрон при вылете из металла.

 . Так как внутренняя энергия идеального газа является функцией только от температуры, то
. Так как внутренняя энергия идеального газа является функцией только от температуры, то .
. является функцией и температуры, и объёма.
является функцией и температуры, и объёма.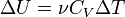 ,
, — количество вещества,
— количество вещества,  — изменение температуры.
— изменение температуры. . Вероятность термодинамическая связана с одной из основных макроскопических характеристик системы энтропией S соотношением Больцмана:
. Вероятность термодинамическая связана с одной из основных макроскопических характеристик системы энтропией S соотношением Больцмана:  , где
, где  — Больцмана постоянная.
— Больцмана постоянная. При учёте соотношений p=m/v=nm_M, M=m_M*Na, R=kNa, принимает вид: p=nkT, с учётом формулы p=2/3n Wk.c.п., получим Wk.c.п.=3/2kT(вывод закона) Для данной массы и молекулярной масс = пост, можно запистать:
При учёте соотношений p=m/v=nm_M, M=m_M*Na, R=kNa, принимает вид: p=nkT, с учётом формулы p=2/3n Wk.c.п., получим Wk.c.п.=3/2kT(вывод закона) Для данной массы и молекулярной масс = пост, можно запистать:
 где — Nчисло частиц газа, —T температура, и —V1V2 и объём газа в начале и конце процесса, —k- Постоянная Больцмана.
где — Nчисло частиц газа, —T температура, и —V1V2 и объём газа в начале и конце процесса, —k- Постоянная Больцмана.


 Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует:
Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует: 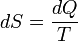 ыше была выведена формула для определения количества теплоты. Перепишем ее в диференциальном виде:
ыше была выведена формула для определения количества теплоты. Перепишем ее в диференциальном виде:  где ν — количество вещества, — молярная теплоемкостью при постоянном объеме.
где ν — количество вещества, — молярная теплоемкостью при постоянном объеме. Серьёзное исследование адиабатических процессов началось в XVIII веке[1].
Серьёзное исследование адиабатических процессов началось в XVIII веке[1]. 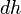 совершать работу[9][10]
совершать работу[9][10]


 — давление газа,
— давление газа,  — малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки
— малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки  на которых расширение одинаково[9].
на которых расширение одинаково[9].

 ,
,  — дифференциальное выражение для работы,
— дифференциальное выражение для работы,  — внешние параметры, которые меняются при совершении работы,
— внешние параметры, которые меняются при совершении работы,  Единица измерения теплоёмкости в системе СИ — Дж/К.Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T:
Единица измерения теплоёмкости в системе СИ — Дж/К.Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T: R = 8.31 Дж/(моль К) — универсальная газовая постоянная.А при постоянном давлении
R = 8.31 Дж/(моль К) — универсальная газовая постоянная.А при постоянном давлении 
 то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо.Можно показать, что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бо́льшим КПД. Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно.
то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо.Можно показать, что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бо́льшим КПД. Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно.


