
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы динамики механической системыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
1. Основные понятия и определения Механическая система – определенным образом выделенная совокупность материальных точек, взаимодействующих друг с другом по закону равенства действия и противодействия. Внешние силы механической системы – силы, с которыми действуют на точки системы тела и точки, в нее не входящие. Внутренние силы механической системы – силы взаимодействия между точками рассматриваемой системы. Центр масс механической системы – геометрическая точка, положение которой определяется радиус-вектором
где Количество движения механической системы – есть векторная сумма количеств движения отдельных точек системы:
где Кинетический момент (главный момент количества движения системы) относительно какой-либо точки – есть векторная сумма моментов количеств движений точек этой системы, взятых относительно точки О:
Кинетический момент системы относительно осей координат:
Кинетический момент твердого тела, вращающегося вокруг неподвижной оси
Кинетическая энергия системы равна сумме кинетических энергий всех материальных точек системы:
Кинетическая энергия твердого тела: а) при поступательном движении:
где б) при вращательном движении:
где в) при плоском движении:
где Элементарная работа переменной силы равна скалярному произведению силы
Работа переменной силы на конечном перемещении по произвольной траектории равна криволинейному интегралу, взятому вдоль дуги кривой
Элементарная работа внешних сил, приложенных к твердому телу: а) поступательное движение:
где б) вращательное движение:
где в) плоское движение:
где
Теорема о движении центра масс механической системы Центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы, действующие на систему
В проекциях на оси координат это равенство эквивалентно трем скалярным:
где Следствия: 1. Одними внутренними силами нельзя изменить характер движения центра масс системы. 2. Если главный вектор внешних сил равен нулю, то центр масс материальной системы находится в покое или движется равномерно и прямолинейно
3. Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс на эту ось не изменяется
4. Пара сил, приложенная к твердому телу не может изменить движение его центра масс. Посредством теоремы можно решать прямые и обратные задачи динамики. Рекомендуемая последовательность действий при решении задач: 1) дать анализ движения тел, входящих в исследуемую механическую систему; 2) изобразить на схеме все внешние силы системы (активные и реакции внешних связей); 3) выбрать систему координат; 4) записать теорему в проекциях на оси декартовых координат; 5) вычислить суммы проекций всех внешних сил системы на оси координат; 6) в зависимости от условий задачи решать прямую, либо обратную задачу динамики.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.10 (0.005 с.) |

 :
: ,
, 
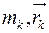 – масса и радиус-вектор материальной точки соответственно,
– масса и радиус-вектор материальной точки соответственно,  – масса системы.
– масса системы. ,
, – скорость материальной точки и цента масс соответственно.
– скорость материальной точки и цента масс соответственно. .
.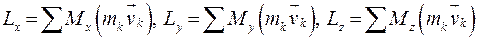 .
. равен произведению момента инерции тела относительно этой оси на проекцию угловой скорости
равен произведению момента инерции тела относительно этой оси на проекцию угловой скорости  :
: .
.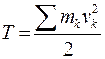 .
.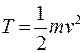 ,
, – масса тела,
– масса тела, 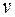 – скорость любой его точки;
– скорость любой его точки; ,
,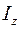 – момент инерции твердого тела относительно оси вращения
– момент инерции твердого тела относительно оси вращения  – угловая скорость вращения;
– угловая скорость вращения; ,
, – модуль скорости центра масс тела,
– модуль скорости центра масс тела,  – момент инерции твердого тела относительно оси
– момент инерции твердого тела относительно оси  и элементарного перемещения
и элементарного перемещения  :
: .
. от элементарной работы:
от элементарной работы: .
. ,
,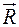 – главный вектор системы сил,
– главный вектор системы сил,  ,
,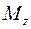 – главный момент системы сил относительно оси вращения
– главный момент системы сил относительно оси вращения  – элементарное угловое перемещение тела;
– элементарное угловое перемещение тела; ,
, – элементарное перемещение полюса О,
– элементарное перемещение полюса О,  – главный момент системы сил относительно оси, проходящей через полюс,
– главный момент системы сил относительно оси, проходящей через полюс,  .
. ,
, ,
,  ,
,  – проекции ускорения центра масс системы.
– проекции ускорения центра масс системы. .
.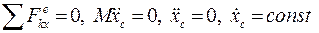 .
.


