Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение теоремы об изменении кинетического момента механической системы к решению задач
Пример 1 Маховик, момент инерции которого I, в начале торможения имел угловую скорость Определить, через сколько времени его угловая скорость уменьшится в два раза, если момент сил сопротивления пропорционален квадрату угловой скорости (коэффициент пропорциональности равен k).
Решение: 1) Механическая система состоит из одного твёрдого тела, вращающегося вокруг неподвижной оси. 2) Так как сила тяжести маховика и сила реакции со стороны вала пересекают ось вращения, их моменты относительно неё равны нулю. 3) Дифференциальные уравнения вращения твёрдого тела относительно неподвижной оси имеет вид:
где Мс момент сил сопротивления, равный Мс = kω 2, тогда: Получили дифференциальные уравнения первого порядка относительно неизвестной функции ω (t). Разделяя переменные, получим: Вычисляем неопределённые интегралы отдельно левой и правой частей:
Произвольную постоянную определяем из начальных условий: t 0=0, ω (t 0)= ω 0: Подставляя значение С 1, получим закон изменения угловой скорости:
Если угловая скорость уменьшится в два раза, то это произойдёт в момент времени:
Пример 2
Решение. 1) Определяем состав исследуемой механической системы. Механическая система состоит из двух твёрдых тел: диска 1 и диска 2. 2) Проводим кинематический анализ движений тел и материальных точек, входящих в исследуемую систему: – диск1 совершает вращательное движение вокруг неподвижной оси Oz; – диск 2 совершает сложное движение, состоящее их двух движений: переносного вращательного вокруг оси Oz с угловой скоростью ω и относительного вращательного вокруг оси BD с постоянной угловой скоростью ω 2. 3) Описываем и обозначаем все внешние силы, действующие на тела и материальные точки, входящие в рассматриваемую систему:
Силы тяжести дисков 4) Записываем теорему об изменении момента количества движения механической системы относительно оси Oz:
где Lz – момент количества движения механической системы; Определяем моменты внешних сил: Тогда из уравнения (1) следует, что Lz (t)=const, т.е. момент количества движения механической системы в момент времени t 0=0 и в момент времени tк равны: Lz (t 0)= Lz (tк). Механическая система состоит из двух твердых тел, поэтому Lz (t)= Lz 1(t)+ Lz 2(t), где Lz 1(t), Lz 2(t) – моменты количеств движения дисков 1 и 2. Диск 1 совершает вращательное движение вокруг неподвижной оси Для однородного диска Диск 2 участвует в двух движениях и момент количества абсолютного движения относительно неподвижной оси равен сумме момента относительно той же оси количества движения его центра масс, в предположении, что в нём сосредоточена вся его масса, и момента относительно оси, проходящей через его центр масс количеств относительного движения диска по отношению к поступательно перемещающимся координатным осям:
где
Подставляя в (2) выражения (4-6) с учётом (3), получаем:
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.166.7 (0.007 с.) |
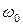 .
. ,
, .
. .
. .
. .
. .
. .
.
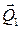 и
и  приложенные в их центрах тяжести и направленные параллельно оси Oz. Реакция подпятника
приложенные в их центрах тяжести и направленные параллельно оси Oz. Реакция подпятника  , приложенная в точке Е и направленная в произвольном направлении в пространстве. Реакция подшипника
, приложенная в точке Е и направленная в произвольном направлении в пространстве. Реакция подшипника  , направленная перпендикулярна оси Oz.
, направленная перпендикулярна оси Oz. (1)
(1) ‑ сумма моментов всех внешних сил, действующих на тела, входящие в механическую систему, относительно той же оси.
‑ сумма моментов всех внешних сил, действующих на тела, входящие в механическую систему, относительно той же оси.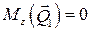 ,
,  , так как эти силы параллельны оси Oz;
, так как эти силы параллельны оси Oz;  ,
,  , так как эти силы пересекают ось Oz.
, так как эти силы пересекают ось Oz. и его момент количества движения равен: Lz 1(t 0)= I 1 ω 0, Lz 1(tк)= I 1 ω, где I 1 – момент инерции диска 1 относительно оси Oz.
и его момент количества движения равен: Lz 1(t 0)= I 1 ω 0, Lz 1(tк)= I 1 ω, где I 1 – момент инерции диска 1 относительно оси Oz. .
. ,
,  , (5)
, (5) ‑ момент инерции диска 2 относительно собственной оси.
‑ момент инерции диска 2 относительно собственной оси. , (6)
, (6) , откуда
, откуда