
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обеспечение механической прочности конструкций РЭССодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обеспечение механической прочности конструкций РЭС Усталостью называется процесс постепенного накопления повреждений в материале детали под действием переменных напряжений. По статистическим данным на МВ приходится от 30% до 50% отказов бортовых РЭС, причем, из них 80% приходится на усталость (установлено в результате испытаний). Приведенные цифры показывают актуальность обеспечения механической прочности конструкций РЭС. Конструкции РЭС, работающие в условиях механических воздействий, должны отвечать требованиям прочности и устойчивости. Определения для этих свойств даны в ГОСТ 16962-71: Вибро- и ударопрочность - способность конструкций выполнять функции и сохранять значения параметров в пределах норм, установленных стандартами, после воздействия механических факторов. Вибро- и удароустойчивость - способность конструкции выполнять заданные функции и сохранять свои параметры в пределах норм, установленных стандартами, во время воздействия механических факторов. Наиболее жёсткие условиями эксплуатации свойственны бортовым ЭС. Например, на них могут воздействовать вибрации с частотами от 20 до 2000 Гц, с уровнями ускорений до 50g. В указанной полосе частот часто не удается избавиться от резонансов элементов конструкции, при которых сильно возрастают ускорения, перемещения и напряжения в них, а затем к их разрушениям. Разработчики РЭС очень часто ограничиваются только стендовыми испытаниями конструкций на прочность и устойчивость, не прибегая к математическому моделированию. Недостатки такого подхода: · сами по себе испытания малоинформативны из-за невозможности установить датчики во многих точках изделия; · испытания не позволяют провести исследования конструкции в критических режимах из-за её разрушения; · результаты испытаний нельзя распространить на другие образцы из-за случайных значений разбросов параметров. Эти проблемы вполне успешно решаются путем математического моделирования на ЭВМ или путем его интеграции с экспериментом. Моделирование РЭС Для определения динамических характеристик РЭС как сложной механической системы (МС) строится ее модель, которая должна быть достаточно точной и в то же время достаточно простой для аналитического исследования.
К важнейшим характеристикам МС относится масса, которая является мерой его инертности, и число степеней свободы, которое определяется количеством координат, необходимым для однозначного задания положения системы в пространстве. Число степеней свободы МС в общем случае является бесконечно большим, так как любое тело состоит из бесконечного числа материальных точек, не имеющих между собой абсолютно жестких связей. При решении инженерных задач, реальная конструкция заменяется моделью с ограниченным числом степеней свободы, которое определяется требуемой точностью результатов. Наиболее простая расчетная модель (РМ), имеющая одну степень свободы, приведена на рисунке 8.2. Ею может быть представлен, например, блок установленный на амортизаторах, если он перемещается только вдоль одной оси - Z. В этой модели вся масса конструкции сосредоточена в элементе массы m, жесткость конструкции - в элементе (пружине) с коэффициентом жесткости k, а демпфирующая связь - в элементе демпфирования b. Поведение такой модели определяется не только параметрами m, k, b и характером действующей силы, но и местом приложения этой силы. В связи с этим, различают модели с кинематическим и силовым возбуждением (рис. 8.2 а, б).
а) б) Рис. 8.2 - Модели с одной степенью свободы: а) с кинематическим
возбуждением; б) с силовым возбуждением.
Рассмотрим более сложные случаи моделирования МС. На рис. 8.3,а представлен эскиз конструкции блока разъемного типа. Его модель может иметь несколько степеней свободы, простейшая из них имеет две степени свободы: - первую степень свободы по отношению к действующим извне вибрациям вносит шасси; - вторую степень свободы вносит печатный узел (ПУ) относительно шасси, поскольку динамические усилия могут быть переданы на печатные платы только через этот элемент конструкции.
Рис. 8.3 – Моделирование разъемной конструкции блока Для элементов конструкций типа стержней модель может быть построена путем многократного повторения простейшей РМ (рис. 8.4). Очевидно, что когда число дискретных элементов в такой модели n®¥, то мы будем иметь модель с распределенными параметрами. Анализ моделей этого типа из-за сложности эффективен только с применением ЭВМ.
Рис. 8.4 – Модели конструктивов типа стержня (а) и пластины (б)
Динамические свойства любой МС существенно зависят от характера восстанавливающих и диссипативных сил. К восстанавливающим силам, относятся силы упругости, возникающие при деформации элементов. Диссипативные силы вызывают необратимое рассеяние энергии механических колебаний. Основные их виды: - силы трения в опорах и сочленениях; - силы сопротивления среды, в которой происходят колебания; - силы внутреннего трения в материалах опор (в амортизаторах). Действие диссипативных сил приводит к затуханию свободных и ограничению вынужденных колебаний.
8.3 Вибрационные воздействия на систему с одной степенью свободы
Случай силового возбуждения Рассмотрим модель, изображенную на рисунке 8.2,б. Кроме возбуждающей силы P=P0 sin wt в этой МС действующая сила инерции Имеется два случая: свободные и для вынужденные колебания. Для свободных колебаний при отсутствии демпфирования ( величина коэффициента демпфирования (затухания)
где
V – мгновенная (начальная) скорость, которая была сообщена массе m в момент времени t=0. Частота w0 не зависит от начальных условий (от начальной скорости V) и определяется только собственными параметрами МС (k и m), поэтому она получила название собственной частоты. С увеличением массы или с уменьшением жесткости пружины k, частота w0 уменьшается. Амплитуда колебаний зависит от начальных условий (от V). Для реальных МС коэффициент
где Учитывая, что величина
Выражение (8.3) описывает затухающее колебание с периодом  (рис. 8.5). (рис. 8.5).
Рис. 8.5 Более точное представление о процессе затухания колебаний дает величина логарифмического декремента затухания: При вынужденных колебаниях на МС постоянно воздействует внешняя сила Р. В этом случае колебательный процесс описывается выражением:
Второе слагаемое в этом выражении – это перемещение при вынужденных колебаниях:
В последних двух формулах используются параметры:
j - начальная фаза вынужденных колебаний. С течением времени (t®¥) колебания МС устанавливаются, а их амплитуда становится равной zв=mZст, откуда m = zв /Zст. Коэффициент динамичности m системыпоказывает, как в зависимости от частотной расстройки изменяется амплитуда вынужденных колебаний относительно ее статического смещения Zст. Из формулы (8.4) следует, что амплитуда перемещения при вынужденных колебаниях зависит не только от параметров МС и возмущающей силы, но и от частоты w. Зависимость коэффициента динамичности m от частоты расстройки является амплитудно-частотной характеристикой (АЧХ) системы при силовом возбуждении (рис. 8.6).
Рис. 8.6 - Зависимость коэффициента динамичности от частотной расстройки при различной степени затухания колебаний.
На частоте
где Для типовых конструкций известны ориентировочные значения m: для микроблоков пенального типа – около 40, для цифровых ячеек на металлических рамках – 10...25, для ячеек на платах из стеклотекстолита – 5...12.
Критерии вибропрочности РЭС В общем виде условиями (критериями) обеспечения вибропрочности конструкции являются: 1) отсутствие в конструкции механических резонансов; 2) ограничение амплитуды виброперемещения и виброскорости значениями, исключающими опасные напряжения и усталостные явления в элементах конструкции; Механические резонансы для конструкций РЭС очень опасны, т.к. при их возникновении многократно возрастают нагрузки на элементы в системе. Поэтому при разработке конструкции стремятся «вывести» собственные частоты ее элементов за пределы диапазона частот внешних воздействий. При расчетах на вибропрочность в первую очередь проверяется выполнение условия: w0 >wв (или ω где w0 - собственная частота элемента; wв, При механических воздействиях на конструкцию могут возникать напряжения связанные с изгибом, кручением и растяжением-сжатием ее элементов. Однако для РЭС, как правило, наиболее опасны изгибные колебания. В этом случае напряжение на изгиб должно отвечать следующему условию
где Ми – изгибающий момент в наиболее опасном сечении элемента конструкции; Wu – момент сопротивления при изгибе. Как уже отмечалось, при знакопеременных напряжениях после некоторого числа циклов нагружения может наступить поломка элемента из-за усталости в материале. В основе усталостных повреждений лежит процесс образования и развития микротрещин в наиболее нагруженном сечении, приводящий, в конечном счете, к разрушению элемента конструкции. Чаще всего в РЭС разрушаются выводы ЭРЭ при наступлении в них высокочастотных резонансов. Если известно максимальное напряжение в выводах, то по кривой усталости для материала (рис. 8.8) можно определить число циклов до разрушения и, таким образом, сделать прогноз долговечности изделия.
Рис. 8.8 – Кривые Велера для меди и алюминия.
Время работы элемента до разрушения выводов можно определить по формуле
где Np - число циклов нагрузки до разрушения; f01 - частота свободных колебаний основного тона элемента. На практике достаточно произвести расчеты вибропрочности только для самых «слабых» элементов конструкции. К ним можно отнести выводы слабо закрепленных ЭРЭ, тонкопроводные монтажные соединения, элементы типа пластин (платы, панели) и др. Виброизоляция Виброизоляция – единственный способ виброзащиты, который дает возможность обеспечить в полосе частот внешних воздействий значение h <1. Он осуществляется путем установки между РЭС и основанием системы амортизаторов (АМ). Амортизатор представляет собой конструкцию, объединяющую упругий и демпфирующий элементы. Упругие силы в АМ создаются пружинами, упругой составляющей жесткости резиновых или полимерных элементов, упругостью металлорезины или троса. Демпфирование в конструкциях АМ осуществляется за счет использования сил сухого или вязкого трения. Примеры конструкций АМ см. на листе РМ-5 (см. ниже). В число основных параметров АМ входят: · номинальная нагрузка амортизатора Pн; · частота свободных колебаний АМ при номинальной нагрузке (вдоль основной оси); · статический прогиб при номинальной нагрузке (zст); · жесткость амортизатора k; · эксплуатационные параметры. Проектирование системы виброизоляции производится в следующей последовательности: 1) выбирают тип АМ с учетом допустимых нагрузок и условий эксплуатации; 2) выбирают схему расстановки (монтажа) АМ; 3) производят статический расчет системы виброизоляции; 4) выбирают конкретный тип АМ с учетом статического расчета; 5) производят динамический расчет системы виброизоляции. АПН - амортизатор пространственного нагружения (это модификация АФД)
Плоскостные или чашечные амортизаторы АП (АЧ)
Сеточный амортизатор
При выборе АМ необходимо выполнять правило: каждый АМ должен работать при номинальной нагрузке, т.к. большая нагрузка приведет к снижению его надежности, а недостаточная - к повышению резонансной частоты. На практике достаточно выполнить условие Pi=(0,7..1,3) Pн. Число амортизаторов должно быть nам³3.
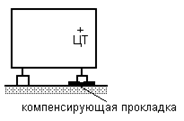
При расстановке АМ обычно используют так называемую рациональную схему, которая должна отвечать следующим требованиям: а) общая статическая грузоподъемность всех АМ равняется весу блока; б) центр тяжести (ЦТ) блока и центр реакции (ЦР) амортизаторов, лежат на одной вертикальной оси. Если ЦТ и ЦР совпадают, то схема расстановки называется абсолютно рациональной.
Примеры схем расстановки амортизаторов.
Рисунок 8.19 - Варианты размещения АМ. Вариант с нижним монтажом (рисунок 8.19,а) получил широкое распространение, так как он позволяет разместить блоки РЭС рядом. Однако если действуют боковые нагрузки, то необходим достаточный зазор между блоками, чтобы избежать соударений. Если ЦТ блока смещен, то для устранения перекосов используют компенсирующие прокладки (рисунок 8.20). Если все амортизаторы имеют одинаковую жесткость Кz, то смещение блока вдоль оси z будет происходить без перекосов, т.е. исключаются повороты относительно осей x и y. Частота собственных колебаний вдоль оси z в этом случае определяется по формуле:
где m -масса блока.
Рисунок 8.20 - Выравнивание блока с помощью прокладки.
Использование в системе АМ у которых Кx =Кy приводит к возникновению в ней сложных (связанных) колебаний. Чтобы избежать этого явления АМ устанавливаются в плоскости ЦТ (рисунок 8.19,б). При этом схема размещения АМ будет абсолютно рациональной. Такой же результат достигается при двустороннем монтаже АМ (рисунок 8.19,в). Монтаж АМ под углом наиболее эффективен при изоляции пространственных колебаний, однако и наиболее сложен, т.к. при небольшом нарушении симметрии в системе возникают связанные между собой колебания. При разработке схемы расстановки АМ их стремятся расположить так, чтобы движения в направлении всех шести степеней свободы были независимыми (чтобы возникали только несвязные колебания). Это дает возможность для каждого АМ обеспечить движение только вдоль оси, т.к. движения и повороты АМ в двух других направлениях для них являются неблагоприятными. Статический расчет системы виброизоляции сводится к определению статических прогибов в амортизаторах и выбору конкретных типов АМ. В результате расчета получают значения координат каждого из амортизаторов, их реакции Рi. и статические прогибы zстi. Если zстi неодинаковы, то производят расчет компенсирующих прокладок. Динамический расчет производится с целью определения эффективности системы виброизоляции. Эффективность определяется следующим соотношением: Э=(1-h)*100%, где h - коэффициент передачи вибраций. Сначала определяют частоту свободных колебаний блока:
где Далее проверяют выполнение условия Фактически это означает, что система амортизации проектируется с запасом 5..6 крат. Если запас обеспечен, то, определив h, рассчитывают величину эффективности Э. Она должна быть не ниже требуемого значения (обычно 90..95%). Если эффективность недостаточна, то выбираются другие АМ.
Обеспечение механической прочности конструкций РЭС
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.241.201 (0.014 с.) |




 , сила упругости пружины Pу=kz и диссипативная сила (сила демпфирования)
, сила упругости пружины Pу=kz и диссипативная сила (сила демпфирования)  .
. =0 ) колебания описываются выражением:
=0 ) колебания описываются выражением: , (8.2)
, (8.2) – частота свободных колебаний;
– частота свободных колебаний; – амплитуда свободных колебаний;
– амплитуда свободных колебаний; ¹0 (он обычно находится в пределах 0,02…0,3). В этом случае колебания системы будут совершаться по закону:
¹0 (он обычно находится в пределах 0,02…0,3). В этом случае колебания системы будут совершаться по закону: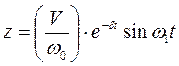 , (8.3)
, (8.3) – собственная частота с демпфированием.
– собственная частота с демпфированием. близка к нулю, на практике считают w1 =w0.
близка к нулю, на практике считают w1 =w0.
 , где
, где  - период затухающих колебаний.
- период затухающих колебаний.
 , (8.4)
, (8.4)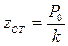 - статический прогиб упругого элемента
- статический прогиб упругого элемента - коэффициент динамичности МС (др. название - коэффициент динамического усиления при силовом возбуждении колебаний);
- коэффициент динамичности МС (др. название - коэффициент динамического усиления при силовом возбуждении колебаний); - коэффициент частотной расстройки;
- коэффициент частотной расстройки;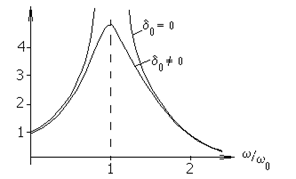
 возникает резонанс, при котором амплитуда вынужденных колебаний достигает максимальной величины. В этом случае коэффициент динамичности равен добротности механической системы Q:
возникает резонанс, при котором амплитуда вынужденных колебаний достигает максимальной величины. В этом случае коэффициент динамичности равен добротности механической системы Q: ,
, – относительный коэффициент демпфирования (затухания) МС;
– относительный коэффициент демпфирования (затухания) МС;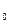 <
<  ) ,
) ,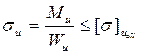 ,
,
 ,
,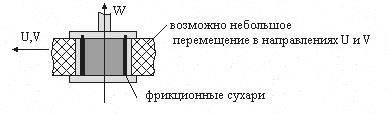 Дополнительные диссипативные силы образуются за счёт трения шайбы о сухари, следовательно, возможны нагрузки не только в направлении W – это является преимуществом перед выше рассмотренными амортизаторами.
Дополнительные диссипативные силы образуются за счёт трения шайбы о сухари, следовательно, возможны нагрузки не только в направлении W – это является преимуществом перед выше рассмотренными амортизаторами.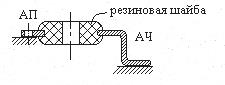 Резиновая шайба определяет упругие силы и упругие свойства амортизатора. Основные параметры этого амортизатора совпадают с параметрами амортизаторов типа АД, кроме требований разрежения.
Резиновая шайба определяет упругие силы и упругие свойства амортизатора. Основные параметры этого амортизатора совпадают с параметрами амортизаторов типа АД, кроме требований разрежения.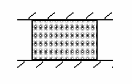 Необычный амортизатор, упругий элемент которого получается прессованием тонкой проволоки (сталь, бериллиевая бронза). При больших деформациях отдельные спирали вытягиваются в одном направлении, что напоминает картинку деформации материалов с длинными волокнами - резины. Поэтому материал упругого элемента сеточного амортизатора обычно называют металлической резиной. Достоинство: небольшие масса и габариты.
Необычный амортизатор, упругий элемент которого получается прессованием тонкой проволоки (сталь, бериллиевая бронза). При больших деформациях отдельные спирали вытягиваются в одном направлении, что напоминает картинку деформации материалов с длинными волокнами - резины. Поэтому материал упругого элемента сеточного амортизатора обычно называют металлической резиной. Достоинство: небольшие масса и габариты.
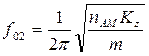 ,
,
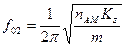
 -суммарная жесткость АМ, величины Кi определяются по справочнику.
-суммарная жесткость АМ, величины Кi определяются по справочнику. , где fн - нижняя частота внешних воздействий.
, где fн - нижняя частота внешних воздействий.


