
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Расчет металлических конструкций по методу предельныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Тема 3. Расчет металлических конструкций по методу предельных состояний Понятие о предельных состояниях конструкций; расчетные ситуации. Расчет конструкций по первой группе предельных состояний. Расчет конструкций по второй группе состояний. Нормативные и расчетные сопротивления
Все строительные конструкции, в том числе и металлические, рассчитываются в настоящее время по методу предельных состояний. В основе метода лежит поня- тие о предельных состояниях конструкций. Под предельными подразумеваются такие состояния, при которых конструкции перестают удовлетворять предъявляе- мым к ним в процессе эксплуатации или при возведении требованиям, заданным в соответствии с назначением и ответственностью сооружений. В металлических конструкциях различают две группы предельных состояний: Предельные состояния первой группы характеризуются потерей несущей способности и полной непригодностью конструкций к эксплуатации. К предельным состояниям первой группы относятся: - разрушение любого характера (вязкое, хрупкое, усталостное); - общая потеря устойчивости формы; - потеря устойчивости положения; - переход конструкции в изменяемую систему; - качественное изменение конфигурации; - развитие пластических деформаций, чрезмерных сдвигов в соединениях и т. д. Выход за границы первой группы предельных состояний означает полную утрату работоспособности конструкции. Предельные состояния второй группы характеризуются непригодностью к нормальной эксплуатации, вследствие появления недопустимых перемещений (прогибов, углов поворота, колебаний и т. д.), а также недопустимого раскрытия трещин (для железобетонных конструкций). В соответствии с действующими нормами [5] при расчете строительных конструкций реализуются две расчетные ситуации: аварийная и установившаяся. Расчет по первой группе предельных состояний направлен на предотв- ращение аварийной расчетной ситуации, которая может возникнуть не более одного раза в течение всего срока эксплуатации конструкции. Расчет по второй группе предельных состояний характеризует установив- шуюся расчетную ситуацию, соответствующую нормативным условиям эксплуатации. Расчет конструкции, направленной на предотвращение предельных состояний первой группы (аварийной расчетной ситуации) выражается неравенством: N ≤ Ф (3.1) где N – усилие в рассматриваемом элементе (продольная сила, изгибающий момент, поперечная сила) Ф – несущая способность элемента При аварийной расчетной ситуации усилие N зависит от предельной расчетной нагрузки Fm, определяемой по формуле:
Fm = F0 ∙ gfm где F0 - характеристическое значение нагрузки, gfm - коэффициент надежности по предельному значению нагрузки, учитывающий возможное отклонение нагрузки в неблагоприятную сторону. Характеристическое значение нагрузки F0 и коэффициент gfm определяют по значениям ДБН [5]. При подсчете нагрузок, как правило, учитывают коэффициент надежности по назначению сооружению gn, зависящий от степени ответственности сооружения Fm = F0 ∙ gfm ∙ gn Значение коэффициента gn приведены в табл. 3.1
Таблица 3.1 Коэффициенты надежности по назначению сооружения gn
Правую часть неравенства (3.1) можно представить в виде Ф = SRygc (3.2) где Ry - расчетное сопротивление стали, установленное по пределу текучести, S - геометрическая характеристика сечения (при растяжении или сжатии – площадь сечения А, при изгибе – момент сопротивления W и т. д.), gc - коэффициент условия работы конструкции, значения которого установлены СНиП [4] и приведены в табл. А 1 приложения А. Подставляя в формулу (3.1) значение (3.2), получим N ≤ SRygc Для растянутых элементов при S = A N ≤ ARygc Разделив левую и правую части неравенства на А, получим условие прочности растянутого элемента
Для изгибаемых элементов при S=W M ≤ WRygc Условие прочности изгибаемого элемента
Формула для проверки устойчивости сжатого элемента
При расчете конструкций, работающих при повторных нагружениях (например, при расчете подкрановых балок) для определения усилий используют циклическую расчетную нагрузку, значение которой определяют по формуле Fc = F0gfcgn где F0 - характеристическое значение крановой нагрузки; gfc - коэффициент надежности по циклическому расчетному значению крановой нагрузки Расчет стальных конструкций, направленный на предотвращение предельных состояний второй группы выражается неравенством d ≤ [ d ], (3.3) где d - деформации или перемещения конструкций, возникающие от эксплуатационного расчетного значения нагрузок; для определения можно использовать методы строительной механики (например, метод Мора, начальных параметров); [ d ] - предельные деформации или перемещения, установленные нормами [4]. Эксплуатационное расчетное значение нагрузки характеризует условия нормальной эксплуатации и определяется по формуле Fl = F0 gfе gn где F0 - характеристическое значение нагрузки, gfе - коэффициент надежности по эксплуатационной расчетной нагрузке. Для изгибаемых элементов (балок, ферм) нормируется относительный прогиб f/l, где f - абсолютный прогиб, l - пролет балки. Формула для проверки жесткости балки на двух опорах имеет вид
где для главных балок для балок настила qe - эксплуатационное расчетное значение нагрузки, определяемое по формуле qe = q0 gfe gn Характеристическое значение нагрузки qe и коэффициент надежности по эксплуатационной расчетной нагрузке gfe принимаются по указаниям норм [5]. Ко второй группе предельных состояний относится также расчет на трещиностойкость в железобетонных конструкциях. Для некоторых материалов, например, пластмасс характерна ползучесть – нестабильность деформаций во времени. В этом случае проверку жесткости конструкций следует выполнять с учетом ползучести. В таких расчетах используют квазипостоянную расчетную нагрузку, значение которой определяют по формуле: Fp = F0 gfp gn где F0 - характеристическое значение квазипостоянной нагрузки; gfp - коэффициент надежности для квазипостоянной расчетной нагрузки.
В металлических конструкциях различают два вида расчетного сопротивления R: - Ry - расчетное сопротивление, установленное по пределу текучести и используемое в расчетах, предполагающих упругую работу материала; - Ru - расчетное сопротивление, установленное по пределу прочности и используемое в расчетах конструкций, где допустимы значительные пластичные деформации. Расчетное сопротивление Ry и Ru определяются по формулам: Ry = Ryn/gm и Ru = Run/gm в которых Ryn и Run - нормативные сопротивления, соответственно равные Ryn = sm Run = sв - где sm - предел текучести, sв - предел прочности (временного сопротивления) материала; gm - коэффициент надежности по материалу, учитывающий изменчивость свойств материала и выборочный характер испытаний образцов по определе- нию sm и sв, а также масштабный фактор – механические характеристики определяются на малых образцах при кратковременном одноосном растяже- нии, в то время как металл работает длительное время в большеразмерных конструкциях. Значение нормативных сопротивлений Ryn = sm и Run = sв, а также значения коэффициента gm устанавливают статистически. Нормативные сопротивления имеют статистическую обеспеченность не менее 0,95, т.е. в 95 случаях из 100 sm и sв будут не менее значений, указанных в сертификате. Коэффициент надежности по материалу gm установлен на основании анализа кривых распределения результатов испытаний стали. Значения этого коэффициента в зависимости от ГОСТ или ТУ на сталь дает табл. 2 СНиП [4]. Значения этого коэффициента изменяются от 1,025 до 1,15. Нормативные Ryn и Run и расчетные Ry и Ru сопротивления для разных марок стали в зависимости от вида проката (лист или фасон) м его толщины представлены в табл. 51 СНиП [4]. В расчетах также используют расчетное сопротивление на сдвиг (срез) Rs =0,58 Ry, на смятие Rp = Ru и др. Нормативные и расчетные сопротивления для некоторых наиболее применяемых марок сталей приведены в табл. 3.2.
Таблица 3.2. Нормативные и расчетные сопротивления стали по ГОСТ 27772-88.
Таким образом, в методе предельных состояний все исходные величины, случайные по своей природе, представляются в нормах некоторыми нормативными значениями, а влияние их изменчивости на конструкцию учитывается соответствующими коэффициентами надежности. Каждый из введенных коэффициентов учитывает изменчивость лишь одной исходной величины (нагрузки, условий работы, свойств материалов, степени ответственности сооружения). Эти коэффициенты часто называют частными, а сам метод расчета по предельным состояниям за рубежом называют методом частных коэффициентов. Литература: [1], с. 50-52; с. 55-58. [2], с. 23-25
Тесты для самоконтроля I. Потеря устойчивости относится к предельным состояниям: 1. I группы; 2. II группы; 3. III группы. II. Коэффициент γm учитывает: 1. условия работы конструкции; 2. изменчивость свойств материала; 3. изменчивость нагрузок. III. Расчетное сопротивление Ry определяют по формуле: 1. Ry = Ryn / γm ; 2. Ry = Run / γn ; 3. Ry = Run / γc. IV. Непригодность конструкций к эксплуатации характеризует предель- ное состояние: 1. I группы; 2. II группы; 3. III группы. V. Коэффициент γn учитывает: 1. Степень ответственности сооружения; 2. изменчивость свойств материала; 3. изменчивость нагрузок. VI. Расчетное сопротивление Ry устанавливают: 1. по пределу упругости; 2. по пределу текучести; 3. по пределу прочности.
VII. Коэффициент γ fm применяют для определения расчетной нагрузки: 1. предельной; 2. эксплуатационной 3. циклической. VIII. Расчет на устойчивость выполняют с учетом расчетной нагрузки: 1. предельной; 2. эксплуатационной 3.циклической. IХ. Хрупкое разрушение относится к предельным состояниям: 1. I группы; 2. II группы; 3. III группы. Х. Для одноэтажных жилых зданий коэффициент γn принимают равным: 1. γn = 1; 2. γn = 0,95; 3. γn = 0,9; ХI. Для особо ответственных зданий коэффициент γn принимают равным: 1. γn = 1; 2. γn = 0,95; 3. γn = 0,9; ХII. Ко второй группе предельных состояний относится расчет: 1. на прочность; 2. на жесткость; 3. на устойчивость. 3.2 Классификация нагрузок. Нагрузка от веса конструкции и грунта. Нагрузки на перекрытия и покрытия зданий. Снеговая нагрузка. Ветровая нагрузка. Сочетания нагрузок. По характеру воздействия нагрузки делятся на: механические и немехани- ческой природы. Механические нагрузки (силы, приложенные к конструкции, или вынужденные деформации) учитываются в расчетах непосредственно. Воздействия немеханической природы, например, влияние агрессивной среды, как правило, в расчете учитывается косвенно. В зависимости от причин возникновения нагрузки и воздействия подразделяют- ся на основные и эпизодические. В зависимости от изменчивости во времени нагрузки и воздействия подразде- ляются на постоянные и переменные (временные). Переменные (временные) нагрузки делятся на: длительные; кратковременные; эпизодические.
Основой для назначения нагрузок являются их характеристические значения. Расчетные значения нагрузок определяются умножением характеристических значений на коэффициент надежности по нагрузке, зависящий от вида нагруже- ния. В зависимости от характера нагрузок и целей расчета используют четыре вида расчетных значений - предельное; эксплуатационное; циклическое; квазипостоянное. Их значения определяют соответственно по формулам: Fm = F0 · γf m · γ n, (3.5) Fe = F0 · γf e · γ n, (3.6) Fc = F0 · γf c · γ n, (3.7) Fp = F0 · γf p · γ n, (3.8) где F0 – характеристическое значение нагрузки; γf m, γf e, γf c, γf p - коэффициенты надежности по нагрузке; γ n – коэффициент надежности по назначению сооружения, учитывающий степень его ответственности (см. табл. 3.1).
К постоянным нагрузкам относят: - вес несущих и ограждающих конструкций здания; - вес и давление грунтов (насыпей, засыпок); - усилие от предварительного напряжения в конструкциях.
К переменным длительным нагрузкам относят: - вес временных перегородок, подливок, подбетонок под оборудование; - вес стационарного оборудования и его заполнения жидкостями, сыпучими телами; - давление газов, жидкостей и сыпучих тел в ёмкостях и трубопроводах; - нагрузки на перекрытия от складируемых материалов в складах, архивах и т.д.; - температурные технологические воздействие от оборудования; - вес слоя воды в водонаполненных покрытиях; - вес отложения производственной пыли; - воздействия, обусловленные деформациями основания без изменения структу- ры грунта; - воздействии, обусловленные изменением влажности, агрессивности среды, усадкой и ползучестью материалов.
К переменным кратковременным нагрузкам относят: - снеговые нагрузки; - ветровые нагрузки; - гололедные нагрузки; - нагрузки от подвижного подъемно-транспортного оборудования, включая мос- товые и подвесные краны; - температурные климатические воздействия; - нагрузки от людей, животных, оборудования на перекрытия жилых, обществен- ных и сельскохозяйственных зданий; - вес людей, ремонтных материалов в зоне обслуживания оборудования; - нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательных режимах.
К эпизодическим нагрузкам относят: - сейсмические воздействия; - взрывные воздействия; - нагрузки аварийные, вызванные нарушениями технологического процесса, по- ломкой оборудования; - нагрузки, обусловленные деформациями основания с коренным изменением структуры грунта (при замачивании просадочных грунтов) или оседанием его в районах горных выработок и в карстовых районах.
Характеристические и расчетные значения эпизодических нагрузок определяются специальными нормативными документами. Характеристическое значение веса конструкций заводского изготовления следует определять на основании каталогов, стандартов, рабочих чертежей или паспортных данных заводов-изготовителей. Для других конструкций (монолит- ный железобетон, кирпичная кладка, грунт) значение веса определяют по проект- ным размерам и плотности материалов. Для железобетона плотность принимается ρ = 2500 кг/м3, для стали ρ = 7850 кг/м3, для кирпичной кладки ρ = 1800 кг/м3.
Постоянная нагрузка может иметь три расчетных значения: - предельное, определяемое по формуле: Fm = F0 · γf m · γ n, - эксплуатационное, определяемое по формуле: Fe = F0 · γf e · γ n, - квазипостоянное, определяемое по формуле: Fp = F0 · γf p · γ n, В приведенных формулах γ n – коэффициент надежности по назначению сооружения (см. табл. (3.1). Значения коэффициента надежности по предельному значению нагрузки γf m принимается по табл.3.3. Значение коэффициент надеж- ности по эксплуатационному значению нагрузки γf e принимается равным 1, т.е γf e = 1; равным 1 принимается также значение коэффициента γf p = 1, исполь- зуемого для определения квазипостоянного расчетного значения нагрузки, приме- няемого в расчетах на ползучесть.
Таблица 3.3 Значение коэффициента γf m
Значения в скобках следует использовать при проверке устойчивости конструкции на опрокидывание и в иных случаях, когда уменьшение веса конструкций и грунтов может ухудшить условия работы конструкции. В таблице 3.4 приведены характеристические значения равномерно распределен- ных нагрузок на перекрытия жилых и общественных зданий.
Таблица 3.4. Нагрузка на перекрытия и покрытия
Продолжение таблицы 3.4.
Предельное эксплуатационное значение нагрузок на перекрытия определяют по формулам: qm = q0· γfm · γn, qe = q0· γfe · γn.
Коэффициенты надежности для предельной нагрузки γfm = 1,3 при q0 < 2кН/м2; при q0 ≥ 2кН/м2 γfm = 1,2. Коэффициент надежности для эксплуатационной нагрузки γfe = 1. Снеговая нагрузка является переменной, для которой установлены три расчетных значения: предельное, эксплуатационное и квазипостоянное. Для расчета без учета реологических свойств материала используют предельное и эксплуатационное расчетные значения снеговой нагрузки. Предельное расчетное значение снеговой нагрузки на горизонтальную проек- цию покрытия определяется по формуле:
Sm = S0 · C · γfm, (3.9) где S0 – характеристическое значение снеговой нагрузки, равное весу снегового покрова на 1м2 поверхности земли. Значения S0 определяются в зависимости от снегового района по карте районирования или по приложению Е [5]. На терри- тории Украины выделено шесть снеговых районов; максимальное значение характеристической нагрузки для каждого из снеговых районов приведены в таблице 3.5. Запорожье расположено в III снеговом районе. Таблица 3.5.- Максимальные значения характеристической снеговой нагрузки
Более точные значения характеристической снеговой нагрузки для некоторых городов Украины приведены в таблице А.3 приложения А. Коэффициент с в формуле (3.9) определяется по формуле: С = μ · Се · Саlt, где: Се – коэффициент учитывающий режим эксплуатации кровли; Саlt – коэффициент географической высоты; μ - коэффициент перехода от веса снегового покрова на поверхности земли к снеговой нагрузке на покрытие, зависящий от формы кровли.
Для зданий с односкатными и двухскатными покрытиями (рис. 3.1) значения коэффициента μ принимают равным:
μ = 1 при α ≤ 250 μ = 0 при α > 600, где α – угол наклона кровли. Варианты 2 и 3 следует учитывать для зданий с двухскатными профилями (профиль б), при этом вариант 2 – 20 0 ≤ α ≤ 300, а вариант 3 – 100 ≤ α ≤ 300 только при наличии ходовых мостиков или аэрацион- ных устройств по коньку покрытия.
с покрытиями других очертаний мож- но найти в приложении Ж [5]. Коэффициент Се в формуле (3.9), учи- тывающий влияние режима эксплуата- ции на накопление снега на кровле (очистку, таяние и др.), устанавливается заданием на проектирование. Для неутеп- ленных покрытий цехов с повышенным тепловыделением при уклонах кровли свыше 3% и обеспечении надлежащего отвода талой воды следует принимать Се =0,8. При отсутствии данных о режи- ме эксплуатации кровли допускается принимать Се =1. Коэффициент Саlt – учитывает географическую высоту Н (км) размещения строительного объекта над уровнем моря. При Н < 0,5км, Саlt = 1, при Н ≥ 0,5км значение Саlt можно определить по формуле: Саlt = 1,4Н + 0,3 Коэффициент γfm по предельному расчетному значению снеговой нагрузки в формуле (3.9) определяется в зависимости от заданного среднего периода повто- ряемости Т по таблице 3.6
Таблица 3.6. Коэффициент γfm по предельному расчетному значению снеговой нагрузки
Промежуточные значения γfm следует определять линейной интерполяцией. Для объектов массового строительства допускается период повторяемости аварийной ситуации Т принимать равным установленному сроку эксплуатации конструкции Теf (табл. А.3, прилож. А). Эксплуатационное расчетное значение снеговой нагрузки определяется по формуле: Se = So · C · γfe, (3.10) где So и C – то же что и в формуле (3.9); γfe – коэффициент надежности по эксплуатационному значению снеговой нагрузки, определяемый по таблице 3.7 в зависимости от доли времени η на протяжении которой могут нарушаться условия второго предель- ного состояния; промежуточное значение γfe следует определять линей- ной интерполяцией. Таблица 3.7. Коэффициент γfe по эксплуатационному значению снеговой нагрузки
Значение η принимается по нормам проектирования конструкций или устанав- ливается заданием на проектирование в зависимости от их назначения, ответствен- ности и следствий выхода за предельное состояние. Для объектов массового строи- тельства допускается принимать η = 0,02 (2% времени от срока службы сооруже- ния).
Ветровая нагрузка является переменной, для которой установлены два расчет- ных значения: предельное и эксплуатационное. Предельное расчетное значение ветровой нагрузки определяется по формуле:
Wm = W0 · C γfm, (3.11)
где С – коэффициент определяемый по формуле (3.12); γfm – коэффициент надежности по предельному значению ветровой нагрузки; W0 - характеристическое значение ветровой нагрузки, равное средней (стати- ческой) составляющей давления ветра на высоте 10м над поверхностью земли. Значение W0 определяется в зависимости от ветрового района по карте районирования или по приложению Е [5]. На территории Украины выделено пять ветровых районов; максимальные характе- ристические значения нагрузки для каждого из ветровых районов приведены в таб- лице 3.8. Запорожье расположено в III ветровом районе.
Таблица 3.8. Максимальные характеристические значения ветровой нагрузки
Более точные значения характеристической ветровой нагрузки для некоторых городов Украины приведены в таблице А.2 прилож. А. Коэффициент С в формуле (3.11) определяется по формуле: С = Саер · Сh · Calt ·Crel · Cdir · Cd (3.12) где Саер – аэродинамический коэффициент; Сh - коэффициент, учитывающий высоту сооружения; Calt – коэффициент географической высоты; Crel – коэффи -циент рельефа; Cdir – коэффициент направления; Cd – коэффициент динамич- ности. Современные нормы предусматривают несколько аэродинамических коэффициентов: - внешнего воздействия Се; - трения Сf; - внутреннего воздействия Ci; - лобового сопротивления Сх; - поперечной силы Су. Значения аэродинамических коэффициентов определяются по приложению И[5] в зависимости от формы сооружения или конструктивного элемента. При расчете рам каркасов зданий обычно используют аэродинамический коэффициент внешнего воздействия Се. На рисунке 3.2 представлены сооружения простейшей формы, схемы ветрового давления на поверхности и аэродинамические коэффициенты внешнего воздействия к ним.
а – отдельно стоящие плоские сплошные конструкции; б – здания с двускатными покрытиями. Рис.3.2. Схемы ветровых нагрузок Для зданий с двускатными покрытиями (рис.3.2,б) аэродинамический коэффициент активного давления Се = + 0,8; значения коэффициентов Се1 и Се2 в зависимости от размеров здания приведены в табл. 3.9, коэффициент Се3 – в табл.3.10. Таблица 3.9. Значения коэффициентов Се1 и Се2
Таблица 3.10. Значения коэффициентов Се3
Знак «плюс» у коэффициентов соответствует направлению давления ветра на поверхность, знак «минус» - от поверхности. Промежуточные значения коэффи-циентов следует определять линейной интерполяцией. Максимальное значение коэффициента для откоса Се3 = 0,6. Коэффициент высоты сооружения Сh учитывает увеличение ветровой нагрузки по высоте здания и зависит от типа окружающей местности и определяется по таблице 3.11. Таблица 3.11. Значения коэффициентов Сh
Типы местности, окружающей сооружение, определяются для каждого расчет- ного направления ветра в отдельности: I – открытые поверхности морей, озер, а также равнины без препятствий, подвер- гающиеся действию ветра на участке длиной не менее 3 км; II – сельская местность с оградами (заборами), небольшими сооружениями, дома- ми и деревьями; III – пригородные и промышленные зоны, протяженные лесные массивы; IV – городские территории, на которых по крайней мере 15% поверхности заняты зданиями, имеющими среднюю высоту более 15 м. Сооружение считается расположенным на местности данного типа для опреде- ленного расчетного направления ветра, если в рассматриваемом направлении такая местность имеется на расстоянии 30 Z при полной высоте сооружения Z < 60м или 2 км при Z > 60м (Z – высота здания). Коэффициент географической высоты Calt учитывает высоту Н (км) размещения строительного объекта над уровнем моря и определяется по формуле:
Calt = 2Н, при Н > 0,5 км, Calt = 1, при Н ≤ 0,5 км.
Коэффициент рельефа Crel учитывает микрорельеф местности вблизи площад- ки, на которой расположен строительный объект, и принимается равным единице за исключением случаев, когда объект строительства расположен на холме или на склоне. Коэффициент направления Cdir учитывает неравномерность ветровой нагрузки по направлению ветра и, как правило, принимается равным единице. Cdir ≠ 1 при- нимается при специальном обосновании только для открытой равнинной местнос- ти. Коэффициент динамичности Cd учитывает, влияние пульсационной составляю- щей ветровой нагрузки и пространственную корреляцию ветрового давления на сооружение. Для сооружений, не требующих расчета динамики ветра Cd = 1. Коэффициент надежности по предельному расчетному значению ветровой наг- рузки γfm определяется в зависимости от заданного среднего периода повторяе- мости Т по таблице 3.12.
Таблица 3.12. Коэффициент надежности по предельному расчетному значению ветровой нагрузки γfm
Промежуточные значения γfm следует определять линейной интерполяцией. Для объектов массового строительства допускается средний период повторяемос - ти Т принимать равным установленному сроку эксплуатации конструкции Тef (по табл.А.3. прилож.А). Эксплуатационное расчетное значение ветровой нагрузки определяется по формуле:
We = Wo · C γfe, (3.13)
где Wo и C – то же, что и в формуле (3.12); γfe – коэффициент надежности по эксплуатационному расчетному значению ветровой
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 8553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.059 с.) |




 (3.4)
(3.4) - предельный относительный прогиб;
- предельный относительный прогиб;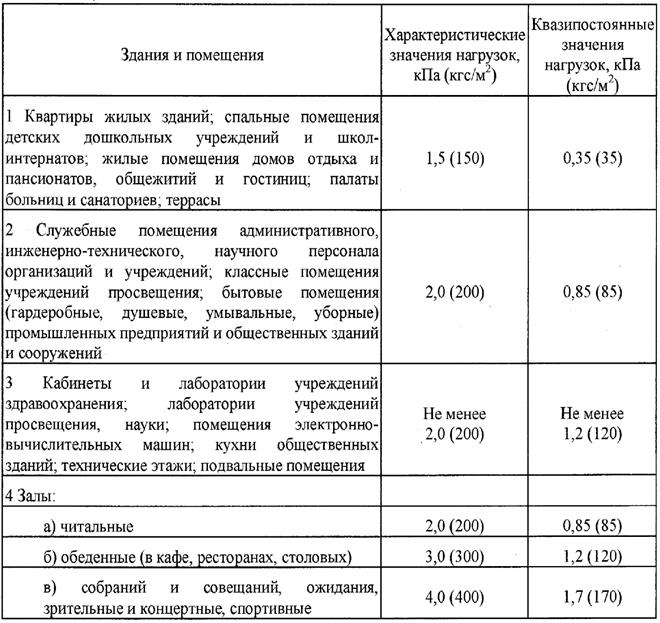



 Значение коэффициента μ для зданий
Значение коэффициента μ для зданий




