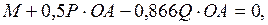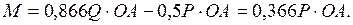Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы аналитической механикиСодержание книги Поиск на нашем сайте 1. Основные определения Механическая система – определенным образом выделенная совокупность материальных точек, взаимодействующих друг с другом по закону равенства действия и противодействия. Связи – любого рода ограничения, налагаемые на положение и скорости материальных точек. Возможные (виртуальные) перемещения точек – бесконечно малые перемещения, допускаемые наложенными в данный момент времени на точку связями. Возможные (виртуальные) перемещения системы – совокупность возможных перемещений точек системы. Число степеней свободы системы – число независимых возможных перемещений точек системы. Идеальные связи – есть связи, сумма элементарных работ реакций которых на любых возможных перемещениях точек системы равна нулю. Обобщенные координаты системы – независимые параметры, однозначно определяющие положение системы в пространстве. Обобщенные силы – коэффициенты, стоящие в выражении суммы работ активных сил при соответствующих обобщенных возможных перемещениях.
2. Принцип возможных перемещений (принцип Лагранжа).
Для равновесия системы материальных точек, подчиненных идеальным стационарным связям, необходимо и достаточно, чтобы сумма работ активных сил на любых возможных перемещениях точек системы равнялась нулю:
где В аналитической форме ПВП имеет вид:
где ПВП применяется для решения задач механики, при рассмотрении равновесия твердых тел и систем твердых тел, а также для определения зависимостей между величинами активных сил. Достоинством ПВП является отсутствие в его формулировке реакций идеальных связей. При наличии наложенных на систему неидеальных связей (негладкие опорные плоскости, поверхности) реакции указанных связей (силы трения) следует добавить к активным силам. ПВП может быть эффективно использован для определения реакций идеальных связей. При этом следует, применяя принцип освобождаемости от связей, отбросить соответствующую связь и заменить ее искомой реакцией. При составлении уравнения равновесия надо к активным силам добавить эту реакцию связи. Количество уравнений равновесия зависит от числа степеней свободы рассматриваемой механической системы. При использовании ПВП для решения задач на равновесие плоских многозвенных механизмов может быть использована аналогия между возможными перемещениями точек системы и их скоростями. Так, для нахождения возможных перемещений заданных точек многозвенных механизмов используется известное из кинематики понятие мгновенного центра скоростей (мгновенный центр вращений) и следствие из теоремы о проекциях скоростей точек плоской фигуры на ось, проходящую через эти точки. Для решения задач с помощью ПВП необходимо, прежде всего, определить число степеней свободы рассматриваемой механической системы. В случае системы с одной степенью свободы рекомендуется следующая последовательность действий: 1) Изобразить на рисунке активные силы; при наличии неидеальных связей добавить к активным силам силы трения. 2) Сообщить возможное перемещение одной из точек системы и выразить возможные перемещения точек приложения сил в зависимости от заданного возможного перемещения; 3) вычислить сумму работ всех указанных в п.1 сил их соответствующих возможных перемещениях их точек приложения, и приравнять эту сумму нулю; 4) решить составленное уравнение равновесия и определить искомую величину.
Пример решения задачи.
Плоский механизм с идеальными связями находится в равновесии под действием сил
Для решения задачи воспользуемся ПВП, согласно которому
где Рассматриваемый механизм имеет одну степень свободы. Его элементы (звенья) совершают следующие виды движений: кривошип ОА и О1В – вращательное движение относительно осей, проходящих через точки О и О1, треугольник АВС и шатун D – поступательное. Чтобы составить уравнение (2.3), сообщим механизму возможное перемещение и введем следующие обозначения для перемещений звеньев, к которым приложены активные силы: Примем за независимое возможное перемещение Сначала найдем возможное перемещение общей для звеньев ОА и АВС точки А. При вращательном движении звена ОА относительно точки О имеем
Направление Для определения возможного перемещения точки С находим мгновенный центр вращения звена АВС, зная линии действия перемещений двух точек А и В этого звена - Тогда линейные возможные перемещения точек А, В и С будут пропорциональны их расстояниям до мгновенного центра вращения:
Находим угловое перемещение звена АВС:
его направление определяется направлением Далее находим и изображаем линейное перемещение точки С
где
В случае необходимости находим по направлению Зная Запишем
Направление Теперь запишем уравнение (1) для механизма:
Так как
откуда
После подстановки исходных данных находим
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 или
или 
 активная сила, приложенная к
активная сила, приложенная к  -й точке системы,
-й точке системы,  - возможное перемещение этой точки.
- возможное перемещение этой точки.
 - проекции активных сил и соответствующих возможных перемещений точек их приложения на оси декартовых координат.
- проекции активных сил и соответствующих возможных перемещений точек их приложения на оси декартовых координат.
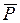 ,
, 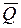 и пары сил с моментом
и пары сил с моментом  , приложенной к звену ОА. Используя принцип возможных перемещений, определить величину момента при следующих исходных данных:
, приложенной к звену ОА. Используя принцип возможных перемещений, определить величину момента при следующих исходных данных: 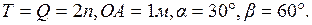 Звено АВС – прямоугольный треугольник с углом при вращении А, равным
Звено АВС – прямоугольный треугольник с углом при вращении А, равным  .
.
 - элементарные работы активных сил на соответствующих возможных перемещениях.
- элементарные работы активных сил на соответствующих возможных перемещениях. - угловое перемещение звена ОА,
- угловое перемещение звена ОА, 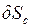 и
и  - линейные перемещения точек C и D.
- линейные перемещения точек C и D. установим кинематические зависимости между указанными возможными перемещениями. Способ их нахождения аналогичен определению скоростей точек при плоском движении.
установим кинематические зависимости между указанными возможными перемещениями. Способ их нахождения аналогичен определению скоростей точек при плоском движении.
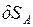 определяются направлением
определяются направлением  . Проводя перпендикуляры к направлениям
. Проводя перпендикуляры к направлениям  . При плоско-параллельном движении все точки звена АВС совершают вращательное движение относительно этой точки.
. При плоско-параллельном движении все точки звена АВС совершают вращательное движение относительно этой точки.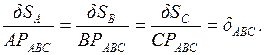

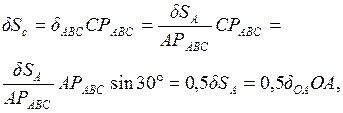
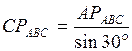 .
.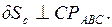 Направление
Направление  определяется направлением
определяется направлением 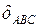 (вращение вокруг точки
(вращение вокруг точки 
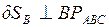 .
.


 за скобки, получим:
за скобки, получим:
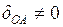 :
: