
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее уравнение динамики движенияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Механической системы
При движении материальной системы, подчиненной идеальным удерживающим связям, сумма работ активных сил и сил инерции на любых возможных перемещениях точек системы равна нулю:
то общее уравнение динамики имеет вид:
Преимущество общего уравнения динамики по сравнению с другими теоремами динамики заключается в том, что в его формулировке отсутствуют реакции идеальных связей. Если не все связи являются идеальными, например, имеются связи с трением, то, применяя общее уравнение динамики, следует к активным силам добавлять реакции, соответствующие неидеальным связям. Вычисление суммы работ сил инерции на возможных перемещениях точек твердого тела производится по формулам:
а) При поступательном движении:
где
б) При вращении вокруг неподвижной оси:
где
в) При плоском движении:
где
При решении задач с помощью общего уравнения динамики рекомендуется следующая последовательность действий: 1) Изобразить на рисунке активные и реакции, соответствующие неидеальным связям (силы трения); 2) Определить главные векторы и главные моменты сил инерции масс системы; 3) Дать возможное перемещение одной из точек системы и выразить возможные перемещения точек приложения всех сил, указанных в 1, 2, через это возможное перемещение. 4) Вычислить сумму работ всех сил на возможных перемещениях точек системы; составить общее уравнение динамики, приравняв в вычисленную сумму работ сил нулю;
5) Определить искомую величину либо провести интегрирование дифференциального уравнения движения.
Пример решения задачи.
Рис.2.1.
Механическая система состоит из ступенчатого шкива 2 (радиусы ступеней R2 и r2), груза 1 и сплошного катка 3, прикрепленных к концам нитей, намотанных на ступени шкива. На шкив при его вращении действует момент сил сопротивления M2 Радиус инерции ступенчатого шкива 2 Дано: R2 = R, r2 = 0,6 R, Р1 = 6Р, Р3 = 3Р, М2 = 0,2 РR, F = 2P, Pz2 = 0,5R, f = 0,1, α = 30˚, β = 60˚, γ = 60˚. Определить: а1 – ускорение груза 1.
1. Материальная система состоит из трех твердых тел и имеет одну степень свободы. Будем считать, что ускорение груза 1
2. Определим вид движений тел, входящих в систему. Груз 1 совершает поступательное движение; шкив 2 совершает вращательное движение вокруг неподвижной оси; каток 3 – совершает плоское движение.
3. Изобразим на рисунке активные силы
4. Определим главные вектора и главные моменты сил инерции масс системы и изобразим их на рисунке.
5. Дадим возможное перемещение центру масс груза 1 -
6. Вычислим сумму работ всех сил, указанных в пунктах 3 и 4, на возможных перемещениях точек системы и составим общее уравнение динамики, приравняв вычисленную сумму работ сил нулю.
После сокращения на заданное возможное перемещение получаем:
Так как
Сила трения скольжения Силу нормальной реакции
Момент инерции шкива 2, поскольку известен его радиус инерции, а каток 3 – сплошной
Окончательно ускорение груза 1 равно
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.183 (0.011 с.) |


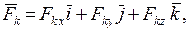
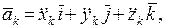



 - равнодействующая сил инерции (
- равнодействующая сил инерции ( );
);  - ускорение любой точки твердого тела;
- ускорение любой точки твердого тела; 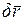 - возможное перемещение любой точки твердого тела.
- возможное перемещение любой точки твердого тела.
 - главный момент сил инерции относительно оси вращения
- главный момент сил инерции относительно оси вращения 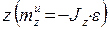 ;
;  - момент инерции твердого тела относительно оси вращения;
- момент инерции твердого тела относительно оси вращения;  - угловое ускорение вращательного движения твердого тела;
- угловое ускорение вращательного движения твердого тела;  - возможное угловое перемещение твердого тела.
- возможное угловое перемещение твердого тела.
 - главный вектор сил инерции
- главный вектор сил инерции  ;
;  - ускорение центра масс твердого тела;
- ускорение центра масс твердого тела; - главный момент сил инерции относительно оси, проходящей через центр масс С твердого тела перпендикулярно плоскости движения
- главный момент сил инерции относительно оси, проходящей через центр масс С твердого тела перпендикулярно плоскости движения  ;
;  - момент инерции твердого тела относительно оси, проходящей через центр масс С перпендикулярно плоскости движения;
- момент инерции твердого тела относительно оси, проходящей через центр масс С перпендикулярно плоскости движения;  - возможное перемещение центра масс С твердого тела;
- возможное перемещение центра масс С твердого тела;  - возможное угловое перемещение твердого тела.
- возможное угловое перемещение твердого тела.
 ρz2, f – коэффициент трения скольжения груза 1 о наклонную плоскость.
ρz2, f – коэффициент трения скольжения груза 1 о наклонную плоскость. направлено вниз по наклонной плоскости.
направлено вниз по наклонной плоскости. и реакции, соответствующие неидеальным связям
и реакции, соответствующие неидеальным связям  .
.

 и выразим возможные перемещения точек приложения всех сил, указанных в пунктах 3 и 4, через это возможное перемещение.
и выразим возможные перемещения точек приложения всех сил, указанных в пунктах 3 и 4, через это возможное перемещение. .
.
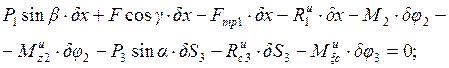
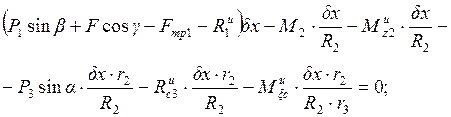




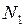 найдем из условия равенства нулю проекций на ось, перпендикулярную направлению движения груза 1 всех сил, действующих на него
найдем из условия равенства нулю проекций на ось, перпендикулярную направлению движения груза 1 всех сил, действующих на него





