
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 17 Первое начало термодинамикиСодержание книги
Поиск на нашем сайте
Вопрос 17 Первое начало термодинамики Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется только ее внутренняя энергия. Внутренняя энергия системы может изменяться в результате совершения над системой работы или сообщения ей теплоты. Например, вдвигая поршень в цилиндр, в котором находится газ, мы сжимаем этот газ, в результате чего его температура повышается, т. е. тем самым увеличивается внутренняя энергия газа. С другой стороны, температуру газа и его внутреннюю энергию можно увеличить за счет сообщения ему некоторого количества теплоты – энергии, переданной системе внешними телами путем теплообмена. Таким образом, существует две формы передачи энергии от одних тел к другим: работа и теплота. Энергия механического движения может превращаться в энергию теплового движения, и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных. Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U1, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U2, совершила работу А над внешней средой, т. е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа – положительной, когда система совершаетее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии U=U2–U1 будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой A, совершенной системой против внешних сил:
или
Уравнение (2.78) выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение (2.78) в дифференциальной форме будет иметь вид
где dU – бесконечно малое изменение внутренней энергии системы, А – элементарная работа, Q – бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а A и Q таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (2.79).
Из формулы (2.78) следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж). Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии dU =0. Тогда, согласно первому началу термодинамики, A=Q, т. е. вечный двигатель первого рода – периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, – невозможен (одна из формулировок первого начала термодинамики). Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде (рисунок 2.19). Рисунок 2.19 Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то производит над ним работу A=Fdl=pSdl=pdV. где S – площадь поршня, Sdl=dV – изменение объема системы. Таким образом,
Полную работу А, совершаемую газом при изменении его объема от V 1 до V 2, найдем интегрированием формулы (2.80):
Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (2.81) справедливо при любых изменениях объема твердых, жидких и газообразных тел. Произведенную при том или ином процессе работу можно изобразить графически с помощью кривой в координатах р, V. Пусть изменение давления газа при его расширении изображается кривой на рисунке 2.20. При увеличении объема на d V совершаемая газом работа равна pdV, т. e. определяется площадью полоски с основанием d V, заштрихованной на рисунке. Поэтому полная работа, совершаемая газом при расширении от объема V1 до объема V2 определяется площадью, ограниченной осью абсцисс, кривой p=f(V) и прямыми V1 и V2. Рисунок 2.20 Графически можно изображать только равновесные процессы – процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны, но чем медленнее процесс протекает, тем он ближе к равновесному. В дальнейшем рассматриваемые процессы будем считать равновесными.
Вопрос 18 Теплоемкость Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: Единица удельной теплоемкости – джоуль на килограмм-кельвин (Дж/(кгК)). Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: где v=m/M – количество вещества. Единица молярной теплоемкости – джоуль на моль-кельвин (Дж/(мольК)). Удельная теплоемкость с связана с молярной Сm соотношением
где М – молярная масса вещества. Если в процессе нагревания вещества его объем или давление поддерживается постоянными, то получают теплоемкости при постоянном объеме и постоянном давлении. Запишем выражение первого начала термодинамики (2.79) для 1 моль газа с учетом значений Q и А:
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (см. (2.80)) и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:
т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К. Подставим, тогда
Если газ нагревается при постоянном давлении, то выражение (2.85) можно записать в виде
Учитывая, что не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна СV (см. (2.86)), и дифференцируя уравнение Клапейрона – Менделеева pVm=RT (2.16) пo T (p = const), получаем
Выражение (2.89) называется уравнением Майера; оно показывает, что CP, всегда больше СV на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (2.87), выражение (2.89) можно записать в вид
Характеристикой для каждого газа является отношение СP к СV:
Молярные теплоемкости одноатомных газов определяются числом степеней свободы и не зависят от температуры в широком интервале температур. У двухатомных газов число степеней свободы зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы. Из экспериментальной зависимости молярной теплоемкости СV водорода (рисунок 2.21) следует, что при низкой температуре (50 К) СV=3/2R, при комнатной – СV=5/2R и при очень высокой – СV=7/2R. Следовательно, при низких температурах наблюдается только поступательное движение молекул, при комнатных – добавляетсяих вращение, а при высоких – к этим двум видам движения добавляются еще колебания молекул. Рисунок 2.21 При вычислении теплоемкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определенный дискретный ряд значений энергий). Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания «замораживается» и не вносят своего вклада в теплоемкость.
Второе начало термодинамики Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов. Кроме того, можно представить множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются. Появление второго начала термодинамики связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие нет. Второе начало термодинамики определяет направление протекания термодинамических процессов.
Используя понятие энтропии и неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает. Можно дать более краткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Здесь существенно, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом (убывать, возрастать, оставаться постоянной). Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах в замкнутой системе энтропия всегда возрастает. Формула Больцмана (2.134) позволяет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Таким образом, формула Больцмана позволяет дать статистическое толкование второго начала термодинамики. Оно, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему. Укажем еще две формулировки второго начала термодинамики: 1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому. Можно довольно просто доказать (предоставим это читателю) эквивалентность формулировок Кельвина и Клаузиуса. Кроме того, показано, что если в замкнутой системе провести воображаемый процесс, противоречащий второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это же доказывает эквивалентность формулировки Клаузиуса (а следовательно, и Кельвина) и статистической формулировки, согласно которой энтропия замкнутой системы не может убывать.
В середине XIX в. возникла проблема так называемой тепловой смерти вселенной. Рассматривая Вселенную как замкнутую систему к применяя к ней второе начало термодинамики, Клаузиус свел его содержание к утверждению, что энтропия Вселенной должна достигнуть своего максимума. Это означает, что со временем все формы движения должны перейти в тепловую. Переход же теплоты от горячих тел к холодным приведет к тому, что температура всех тел во Вселенной сравняется, т. е. наступит полное тепловое равновесие и все процессы во Вселенной прекратятся – наступит тепловая смерть Вселенной. Ошибочность вывода о тепловой смерти заключается в том, что бессмысленно применять второе начало термодинамики к незамкнутым системам, например к такой безграничной в бесконечно развивающейся системе, как Вселенная. Первые два начала термодинамики дают недостаточно сведений о поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом термодинамики, или теоремой Нернста – Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина: Так как энтропия определяется с точностью до аддитивной постоянной, то эту постоянную удобно взять равной нулю. Отметим, однако, что это произвольное допущение, поскольку энтропия по своей сущности всегда определяется с точностью до аддитивной постоянной. Из теоремы Нернста – Планка следует, что теплоемкости СP и СV при 0 К равны нулю. Закон Кулона Точечным называется заряд, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует. Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними:
где k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной. В случае разноименных зарядов возникает притяжение (F<0), в случае одноименных зарядов - отталкивание (F>0). Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид:
где F В СИ коэффициент пропорциональности равен k=
Величина
Формула (3.7) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
Вопрос 26 Потенциал Работа консервативны сил совершается за счет убыли потенциальной энергии. Работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q в начальной и конечной точках поля заряда Q:
Отношение U/Q Потенциал Потенциал поля, создаваемого точечным зарядом Q, равен Работа, совершаемая силами электростатического поля при перемещении заряда Q
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля при перемещении положительного единичного заряда из точки 1 в точку 2.
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения. Если перемещать заряд Q A откуда
Таким образом, потенциал — физическая величина, определяемая работой по перемещению положительного единичного заряда при удалении его из данной точки поля в бесконечность. Единица потенциала — вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В= 1 Дж/Кл). Если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов. Элементарная работа сил электростатического поля переноса положительного единичного точечного заряда на пути dl равна E d l = E Интеграл Формула справедлива только для электростатического поля.
Величину
называют электроемкостью уединённого проводника. Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала. Единица электроемкости — фарад (Ф). Емкость конденсатора - это физическая величина, равная отношению заряда Q,, накопленного в конденсаторе, к разности потенциалов (
Емкость плоского конденсатора:
Вопрос 17 Первое начало термодинамики Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется только ее внутренняя энергия. Внутренняя энергия системы может изменяться в результате совершения над системой работы или сообщения ей теплоты. Например, вдвигая поршень в цилиндр, в котором находится газ, мы сжимаем этот газ, в результате чего его температура повышается, т. е. тем самым увеличивается внутренняя энергия газа. С другой стороны, температуру газа и его внутреннюю энергию можно увеличить за счет сообщения ему некоторого количества теплоты – энергии, переданной системе внешними телами путем теплообмена. Таким образом, существует две формы передачи энергии от одних тел к другим: работа и теплота. Энергия механического движения может превращаться в энергию теплового движения, и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных. Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U1, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U2, совершила работу А над внешней средой, т. е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа – положительной, когда система совершаетее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии U=U2–U1 будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой A, совершенной системой против внешних сил:
или
Уравнение (2.78) выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение (2.78) в дифференциальной форме будет иметь вид
где dU – бесконечно малое изменение внутренней энергии системы, А – элементарная работа, Q – бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а A и Q таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (2.79). Из формулы (2.78) следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж). Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии dU =0. Тогда, согласно первому началу термодинамики, A=Q, т. е. вечный двигатель первого рода – периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, – невозможен (одна из формулировок первого начала термодинамики). Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде (рисунок 2.19). Рисунок 2.19 Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то производит над ним работу A=Fdl=pSdl=pdV. где S – площадь поршня, Sdl=dV – изменение объема системы. Таким образом,
Полную работу А, совершаемую газом при изменении его объема от V 1 до V 2, найдем интегрированием формулы (2.80):
Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (2.81) справедливо при любых изменениях объема твердых, жидких и газообразных тел. Произведенную при том или ином процессе работу можно изобразить графически с помощью кривой в координатах р, V. Пусть изменение давления газа при его расширении изображается кривой на рисунке 2.20. При увеличении объема на d V совершаемая газом работа равна pdV, т. e. определяется площадью полоски с основанием d V, заштрихованной на рисунке. Поэтому полная работа, совершаемая газом при расширении от объема V1 до объема V2 определяется площадью, ограниченной осью абсцисс, кривой p=f(V) и прямыми V1 и V2. Рисунок 2.20 Графически можно изображать только равновесные процессы – процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны, но чем медленнее процесс протекает, тем он ближе к равновесному. В дальнейшем рассматриваемые процессы будем считать равновесными.
Вопрос 18 Теплоемкость Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: Единица удельной теплоемкости – джоуль на килограмм-кельвин (Дж/(кгК)). Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: где v=m/M – количество вещества. Единица молярной теплоемкости – джоуль на моль-кельвин (Дж/(мольК)). Удельная теплоемкость с связана с молярной Сm соотношением
где М – молярная масса вещества. Если в процессе нагревания вещества его объем или давление поддерживается постоянными, то получают теплоемкости при постоянном объеме и постоянном давлении. Запишем выражение первого начала термодинамики (2.79) для 1 моль газа с учетом значений Q и А:
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (см. (2.80)) и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:
т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К. Подставим, тогда
Если газ нагревается при постоянном давлении, то выражение (2.85) можно записать в виде
Учитывая, что не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна СV (см. (2.86)), и дифференцируя уравнение Клапейрона – Менделеева pVm=RT (2.16) пo T (p = const), получаем
Выражение (2.89) называется уравнением Майера; оно показывает, что CP, всегда больше СV на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (2.87), выражение (2.89) можно записать в вид
Характеристикой для каждого газа является отношение СP к СV:
Молярные теплоемкости одноатомных газов определяются числом степеней свободы и не зависят от температуры в широком интервале температур. У двухатомных газов число степеней свободы зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы. Из экспериментальной зависимости молярной теплоемкости СV водорода (рисунок 2.21) следует, что при низкой температуре (50 К) СV=3/2R, при комнатной – СV=5/2R и при очень высокой – СV=7/2R. Следовательно, при низких температурах наблюдается только поступательное движение молекул, при комнатных – добавляетсяих вращение, а при высоких – к этим двум видам движения добавляются еще колебания молекул. Рисунок 2.21 При вычислении теплоемкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определенный дискретный ряд значений энергий). Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания «замораживается» и не вносят своего вклада в теплоемкость.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.246.21 (0.015 с.) |



 F
F  =
= 
 — сила, действующая на заряд Q
— сила, действующая на заряд Q  со стороны заряда Q
со стороны заряда Q  , r
, r  = - F
= - F  Тогда закон Кулона запишется в окончательном виде:
Тогда закон Кулона запишется в окончательном виде:
 относится к числу фундаментальных физических постоянных и называется электрической постоянной:
относится к числу фундаментальных физических постоянных и называется электрической постоянной:  =8,8510-12Кл2/(Hм2) или
=8,8510-12Кл2/(Hм2) или  =8,85110-12 Ф/м, где фарад (Ф) — единица электрической емкости. Тогда
=8,85110-12 Ф/м, где фарад (Ф) — единица электрической емкости. Тогда  =9109 м/Ф.
=9109 м/Ф.
 = U
= U  не зависит от Q
не зависит от Q 
 в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией положительного единичного заряда, помещенного в эту точку.
в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией положительного единичного заряда, помещенного в эту точку.
 ), не зависит от траектории перемещения
), не зависит от траектории перемещения
 =
=  =
= 
 = Q
= Q 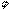 ,
,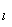 dl, где E
dl, где E 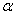 — проекция вектора Е на направление элементарного перемещения.
— проекция вектора Е на направление элементарного перемещения.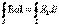 называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю, следовательно, линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и заканчиваются на зарядах или же уходят в бесконечность.
называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю, следовательно, линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и заканчиваются на зарядах или же уходят в бесконечность. ) между его обкладками:
) между его обкладками:



