
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное и тангенциальное ускорениеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Кинематика Основные понятия Материальная точка: тело, размерами которого можно пренебречь при описании его движения. Система материальных точек и число степеней свободы м.т. (системы м.т.) – число независимых параметров, необходимых для фиксации ее положения в пространстве. Выбор этих параметров может быть проведен по-разному, однако их число от конкретного выбора не зависит, являясь важнейшей инвариантной характеристикой системы. Чем больше у механической системы степеней свободы, тем сложнее оказывается математический анализ закона ее движения.Материальную точку классической механики можно рассматривать как простейшие механические объекты, обладающие наименьшим числом степеней свободы. Это число совпадает с размерностью реального физического пространства, т.е. равно трем. Абсолютно твердое тело: тело, у которого размеры и форма не меняются. Тело отсчета: тело, относительно которого определяют положение других тел. Система отсчета: система координат, связанная с телом отсчета и способ измерения времени (часы). Радиус-вектор r - это вектор, проведенный из начала координат в какую-либо точку пространства. Зависимость радиуса-вектора от времени определяет кинематический закон движения тела Компоненты радиус-вектора В трёхмерном пространстве на плоскости
- x, y, z - компоненты радиуса - вектора. Очевидно, они же являются координатами материальной точки. Модуль радиус-вектора Траектория - это линия, описываемая материальной точкой при ее движении. Путь - длина отрезка траектории. Перемещение - вектор, проведенный из начального положения материальной точки в ее конечное положение.
Скорость всегда направлена по касательной к траектории Компоненты скорости Вектор скорости
компоненты скорости равны производным соответствующих координат по времени:
Средняя скорость. По теореме о среднем имеем: Средний модуль скорости за время D t = t 2- t 1 Средний вектор скорости за время D t = t 2- t 1 Модуль скорости - производная пути по времени.
По теореме Пифагора: Вычисление пройденного пути: путь - это определенный интеграл от модуля скорости по времени:
v1 в течение отрезка Δti приблизительно постоянны, если Δt достаточно мало.
Ускорение - это производная скорости по времени.
Ускорение - вторая производная радиуса-вектора по времени. Производную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение - это скорость изменения скорости. Выбор системы отсчета. Нахождение закона движения существенно осложняется, когда речь идет о взаимном расположении движущихся тел – то, с чем мы имеем дело в механике. Если мы хотим не только проследить за взаимным расположением движущихся предметов, но и установить причину их движения, а также определить закон движения, то мы должны выбирать систему отсчета вполне определенным образом. Из всех возможных систем отсчета в механике привилегированную роль играют так называемые инерциальные системы отсчета. Инерциальную систему отсчета можно определить как систему отсчета, в которой справедливо первое Начало механики (первый закон Ньютона): всякое тело сохраняет состояние покоя или состояние равномерного прямолинейного движения пока какие-либо силы не выведут его из этого состояния. Само первое Начало можно рассматривать как утверждение того факта, что инерциальные системы существуют в природе.
Преимущество инерциальной системы отсчета впервые в истории науки обнаружилось при разрешении спора между сторонниками геоцентрической и гелиоцентрической систем мироздания. Переход от господствовавшей в средние века геоцентрической системы к гелиоцентрической означал переход от неинерциальной системы отсчета к инерциальной и дал возможность не только описывать взаимное расположение небесных тел, но и выяснить причину и законы их движения на основе открытого Ньютоном закона всемирного тяготения. Понятие инерциальной системы -- это идеализированное понятие. Любая реально выбранная система отсчета всегда имеет какую-то "примесь" неинерциальности. Весь вопрос в том, насколько слабы эффекты, вызываемые неинерциальностью системы отсчета, и можно ли ими пренебречь при решении конкретной задачи. Так, например, система отсчета, связанная с Землей, совершенно непригодна для задач небесной механики, но полностью удовлетворяет нуждам внешней баллистики (расчет полета снарядов). Однако, при расчете движения спутников эффект неинерциальности системы земного отсчета становится уже заметным и может быть учтен как малая поправка. Если установлено существование некоторой инерциальной системы отсчета, то любая другая система отсчета, движущаяся по отношению к первой прямолинейно с постоянной скоростью, также будет инерциальной. Действительно, совершенно очевидно, что для любой такой системы отсчета будет справедливо первое Начало механики, а это означает, по определению, ее инерциальность. При переходе от одной инерциальной системы к другой, движущейся относительно ее, скорость материального тела изменяется на величину относительной скорости координатных систем, а ускорение остается неизменным. Вследствие этого, второй закон Ньютона, являющийся основным законом механики, имеет один и тот же вид во всех инерциальных системах отсчета. Здесь мы подошли к формулировке одного из основных принципов механики.
Динамика материальной точки Второй закон Ньютона Скорость изменения импульса равна действующей на материальную точку результирующей силе:.
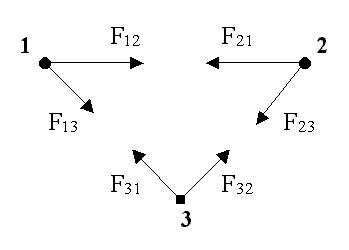
Третий закон Ньютона Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Пример - взаимодействие двух электрических зарядов:
Уравнения движения. Второй закон механики (з. Ньютона) позволяет записать уравнение движения тела (м.т.): это уравнение вида Для системы N тел необходимо интегрировать 3 N уравнений с 6 N начальными условиями. Сложность этих уравнений определяется видом сил. В общем случае силы могут зависеть от координат всех тел, их скоростей и времени (всего 6 N +1 переменных). Аналитически эта задача разрешима только для системы двух тел, взаимодействующих гравитационно – задача Кеплера. Уже для трех тел (Солнце, Земля, Луна) эта задача в квадратурах не разрешима. Пример интегрирования уравнений движения в одномерном случае: прыжок парашютиста. Человек массы m прыгает с высоты h 0, а через t секунд раскрывает парашют – пример тела, двигающегося в вязкой среде с коэффициентом аэродинамического сопротивления r. Кроме постоянной силы тяжести на него действует аэродинамическая сила сопротивления воздуха, пропорциональная скорости Уравнение движения запишем в виде Начальная высота h 0 = 1000 м, начальная скорость V 0 = 0.
Законы сохранения Внутренние и внешние силы
Замкнутая система
Импульс системы материальных точек - это векторная сумма импульсов всех материальных точек, входящих в систему
Закон сохранения импульса Импульс замкнутой системы сохраняется, т.е. не изменяется со временем. На рисунке изображена замкнутая система, состоящая из трех тел.
По II закону Ньютона, примененному к каждому телу рассматриваемой замкнутой системы, имеем:
Если система не замкнута, но внешние силы не действуют на неё вдоль каких-либо осей, то соответствующие компоненты импульса сохраняются, например:
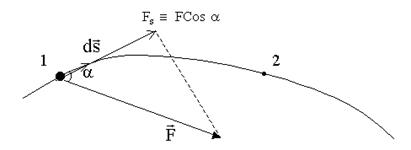
Работа Работа постоянной силы
Элементарная работа
Работа переменной силы
Единица измерения работы [A]=[F].[s]= H.м = джоуль, Дж Мощность P - это скорость совершения работы,
Единица мощности
Кинетическая энергия (теорема о кинетической энергии)
преобразуя левую часть,
получим
Кинетическая энергия
Таким образом элементарная работа, совершаемая над телом, равна элементарному приращению его кинетической энергии. При интегрировании вдоль траектории частицы, от точки 1 до точки 2, мы получим:
Работа результирующей силы идет на приращение кинетической энергии материальной точки (работа совершается за счет убыли кинетической энергии). Консервативные и неконсервативные силы Угловая скорость
Теорема Штейнера
где I0 - момент инерции относительно оси OО, Моменты инерции I0 для некоторых тел
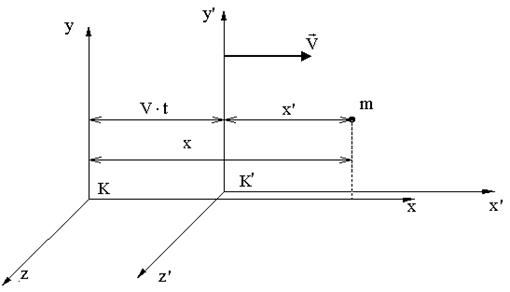
СТО Преобразования Галилея - это уравнения, связывающие координаты и время некоторого СОБЫТИЯ в двух инерциальных системах отсчета. СОБЫТИЕ определяется местом, где оно произошло (координаты x, y, z), и моментом времени t, когда произошло событие. Событие полностью определено, если заданы четыре числа: x,y,z,t - координаты события. Пусть материальная точка m в системе отсчета К в момент времени t имела координаты x, y, z, т.е. в системе К заданы координаты события - t, х, y, z. Найдем координаты t', x', y', z' этого события в системе отсчета К', которая движется относительно системы К равномерно и прямолинейно вдоль оси х со скоростью Выберем начало отсчета времени так, чтобы в момент времени t = 0 начала координат совпадали. Оси х и х' направлены вдоль одной прямой, а оси у и у', z и z' - параллельны.
Тогда из рисунка ОЧЕВИДНО: x = x'+Vt.
x = x' + Vt, Принцип относительности Галилея: Постулаты С.Т.О. Механика больших скоростей, специальная теория относительности (С.Т.О.), I. Принцип относительности (Эйнштейна), согласно которому никакими физическими опытами нельзя установить, покоится ли данная система отсчета, либо движется равномерно и прямолинейно. Другая формулировка: Все законы природы одинаково формулируются для всех инерциальных систем отсчета. II. Принцип постоянства скорости света: cкорость света в вакууме во всех инерциальных системах отсчета одинакова и не зависит ни от движения источника, ни от движения приемника света. Преобразования Лоренца - это уравнения, связывающие координаты и время некоторого события в двух инерциальных системах отсчета. В отличие от преобразований Галилея преобразования Лоренца не должны противоречить постулатам С.Т.О.: необнаружимости абсолютного движения и постоянству скорости света. При скорости движения системы отсчета V<< c преобразования Лоренца должны переходить в преобразования Галилея. Вывод преобразований Лоренца (не обязательно) Рассмотрим две системы отсчета. Одна система К - неподвижна, другая К' движется вдоль оси х со скоростью V. При t =0 начала координат совпадали. Пусть наблюдатель в К системе проделал опыты по изучению движения тела и получил законы движения по каждой координате: x = x (t); y = y (t); z = z (t). Тогда наблюдателю в К' системе не надо проводить опыты, законы движения в своей системе координат он может получить по формулам преобразования Лоренца.
Такие преобразования сохраняют вид уравнения фронта световой волны, сфера преобразуется в сферу, в соответствии с постулатами С.Т.О.
тогда преобразования Лоренца запишутся так:
Релятивистская механика должна быть построена таким образом, чтобы уравнения движения не менялись при переходе из одной инерциальной системы отсчета в другую, т.е. были инвариантны относительно преобразований Лоренца. Следствия из преобразований Лоренца Релятивистская динамика Релятивистский импульс В классической механике В релятивистской механике, где v → c,
Выражение для релятивистского импульса отличается от классического множителем γ. Энергия покоя При скорости материальной точки v=0
Масса покоя Скорость света Интервал Энергетический инвариант Из этого следует, что
т.е. не зависит от выбора системы отсчета.
Кинематика Основные понятия Материальная точка: тело, размерами которого можно пренебречь при описании его движения. Система материальных точек и число степеней свободы м.т. (системы м.т.) – число независимых параметров, необходимых для фиксации ее положения в пространстве. Выбор этих параметров может быть проведен по-разному, однако их число от конкретного выбора не зависит, являясь важнейшей инвариантной характеристикой системы. Чем больше у механической системы степеней свободы, тем сложнее оказывается математический анализ закона ее движения.Материальную точку классической механики можно рассматривать как простейшие механические объекты, обладающие наименьшим числом степеней свободы. Это число совпадает с размерностью реального физического пространства, т.е. равно трем. Абсолютно твердое тело: тело, у которого размеры и форма не меняются. Тело отсчета: тело, относительно которого определяют положение других тел. Система отсчета: система координат, связанная с телом отсчета и способ измерения времени (часы). Радиус-вектор r - это вектор, проведенный из начала координат в какую-либо точку пространства. Зависимость радиуса-вектора от времени определяет кинематический закон движения тела Компоненты радиус-вектора В трёхмерном пространстве на плоскости
- x, y, z - компоненты радиуса - вектора. Очевидно, они же являются координатами материальной точки. Модуль радиус-вектора Траектория - это линия, описываемая материальной точкой при ее движении. Путь - длина отрезка траектории. Перемещение - вектор, проведенный из начального положения материальной точки в ее конечное положение.
Скорость всегда направлена по касательной к траектории Компоненты скорости Вектор скорости
компоненты скорости равны производным соответствующих координат по времени:
Средняя скорость. По теореме о среднем имеем: Средний модуль скорости за время D t = t 2- t 1 Средний вектор скорости за время D t = t 2- t 1 Модуль скорости - производная пути по времени.
По теореме Пифагора: Вычисление пройденного пути: путь - это определенный интеграл от модуля скорости по времени:
v1 в течение отрезка Δti приблизительно постоянны, если Δt достаточно мало.
Ускорение - это производная скорости по времени.
Ускорение - вторая производная радиуса-вектора по времени. Производную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение - это скорость изменения скорости. Нормальное и тангенциальное ускорение Направим единичный вектор
Тогда (по правилу нахождения производной от произведения). Первый член, нормальное ускорение,
показывает быстроту изменения направления скорости. Второй, тангенциальное ускорение,
направлен вдоль скорости и показывает быстроту изменения ее модуля. Направление и величину нормального ускорения найдем для частного случая равномерного движения материальной точки по окружности:
Направлен
Нормальное ускорение направлено по нормали к скорости, его модуль:
Для движения по произвольной кривой R - радиус кривизны траектории - не будет величиной постоянной.
Основная задача кинематики: по заданной зависимости ускорения от времени Для одномерного движения: 1) Из определения ускорения 2) Из определения ускорения Таким образом, для нахождения закона движения тела по каждой координате необходимо задать шесть констант – три начальных координаты: x 0, y 0, z 0 и три начальных проекций скорости Vx 0, Vy 0, Vz 0 – всего 6 констант интегрирования, определяющих начальное положение тела (м.т.) – начальные условия. Для наиболее простого случая Вопрос о зависимости ускорения от времени Выбор системы отсчета. Нахождение закона движения существенно осложняется, когда речь идет о взаимном расположении движущихся тел – то, с чем мы имеем дело в механике. Если мы хотим не только проследить за взаимным расположением движущихся предметов, но и установить причину их движения, а также определить закон движения, то мы должны выбирать систему отсчета вполне определенным образом. Из всех возможных систем отсчета в механике привилегированную роль играют так называемые инерциальные системы отсчета. Инерциальную систему отсчета можно определить как систему отсчета, в которой справедливо первое Начало механики (первый закон Ньютона): всякое тело сохраняет состояние покоя или состояние равномерного прямолинейного движения пока какие-либо силы не выведут его из этого состояния. Само первое Начало можно рассматривать как утверждение того факта, что инерциальные системы существуют в природе.
Преимущество инерциальной системы отсчета впервые в истории науки обнаружилось при разрешении спора между сторонниками геоцентрической и гелиоцентрической систем мироздания. Переход от господствовавшей в средние века геоцентрической системы к гелиоцентрической означал переход от неинерциальной системы отсчета к инерциальной и дал возможность не только описывать взаимное расположение небесных тел, но и выяснить причину и законы их движения на основе открытого Ньютоном закона всемирного тяготения. Понятие инерциальной системы -- это идеализированное понятие. Любая реально выбранная система отсчета всегда имеет какую-то "примесь" неинерциальности. Весь вопрос в том, насколько слабы эффекты, вызываемые неинерциальностью системы отсчета, и можно ли ими пренебречь при решении конкретной задачи. Так, например, система отсчета, связанная с Землей, совершенно непригодна для задач небесной механики, но полностью удовлетворяет нуждам внешней баллистики (расчет полета снарядов). Однако, при расчете движения спутников эффект неинерциальности системы земного отсчета становится уже заметным и может быть учтен как малая поправка. Если установлено существование некоторой инерциальной системы отсчета, то любая другая система отсчета, движущаяся по отношению к первой прямолинейно с постоянной скоростью, также будет инерциальной. Действительно, совершенно очевидно, что для любой такой системы отсчета будет справедливо первое Начало механики, а это означает, по определению, ее инерциальность. При переходе от одной инерциальной системы к другой, движущейся относительно ее, скорость материального тела изменяется на величину относительной скорости координатных систем, а ускорение остается неизменным. Вследствие этого, второй закон Ньютона, являющийся основным законом механики, имеет один и тот же вид во всех инерциальных системах отсчета. Здесь мы подошли к формулировке одного из основных принципов механики.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1080; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.76 (0.01 с.) |

 . Это векторное уравнение эквивалентно заданию трёх скалярных уравнений
. Это векторное уравнение эквивалентно заданию трёх скалярных уравнений  ,
,  ,
,  , которые также называются кинематическими законами движения.
, которые также называются кинематическими законами движения.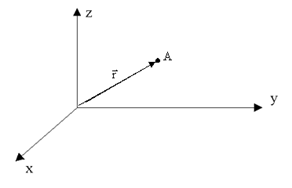

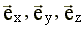 единичные векторы или орты, направленные по осям x, y, z соответственно;
единичные векторы или орты, направленные по осям x, y, z соответственно; - по теореме Пифагора.
- по теореме Пифагора.

 материальной точки M, движущейся по плоскости x, y:
материальной точки M, движущейся по плоскости x, y:
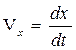 ;
;  ;
;  . Зная проекции, мы всегда построим вектор скорости.
. Зная проекции, мы всегда построим вектор скорости.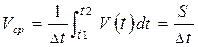

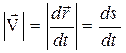 .
.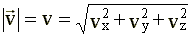 .
.

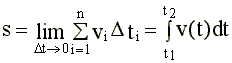 ,
,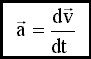 или:
или: 
 , где
, где 

 при m ≠ m(t)
при m ≠ m(t) т.к
т.к то
то
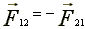

 , из которого путем двойного интегрирования находится закон движения
, из которого путем двойного интегрирования находится закон движения  при задании шести начальных условий. Это уравнение эквивалентно трем скалярным неоднородным дифференциальным уравнениям второго порядка (в общем случае трёхмерного движения).
при задании шести начальных условий. Это уравнение эквивалентно трем скалярным неоднородным дифференциальным уравнениям второго порядка (в общем случае трёхмерного движения). .
. . Перепишем в виде, удобном для интегрирования и проинтегрируем,
. Перепишем в виде, удобном для интегрирования и проинтегрируем, 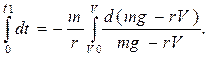 В результате найдём зависимость времени от скорости
В результате найдём зависимость времени от скорости  Обратная зависимость скорости от времени
Обратная зависимость скорости от времени  , где
, где  – характерное время. Зависимость y -вой координаты от времени
– характерное время. Зависимость y -вой координаты от времени  .
.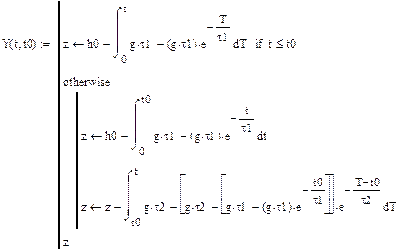



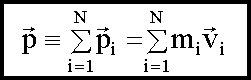



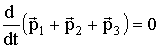
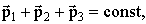







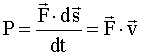
 .
.

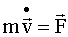
 - справа на
- справа на 
 .
.
 .
.
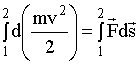



 , или
, или  . Псевдовектор
. Псевдовектор  направлен так же, как и псевдовектор
направлен так же, как и псевдовектор  .
Угловое ускорение
.
Угловое ускорение


 ,
, ,
,
 ,
,
 ,
,
 ,
,
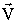 .
.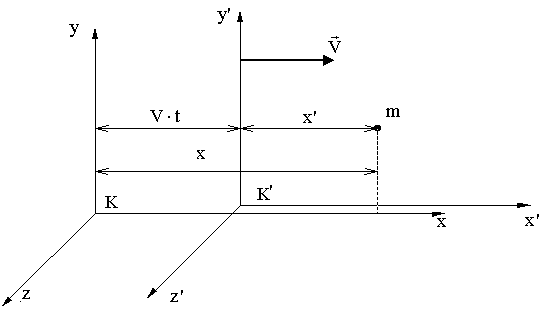

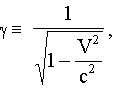
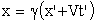 ;
;
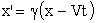 ;
;
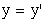 ;
;
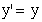 ;
;
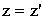 ;
;
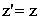 ;
;
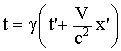
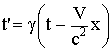 .
.
 , при v << c.
, при v << c. .
.
 - inv, инвариант,
- inv, инвариант,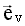 вдоль вектора скорости:
вдоль вектора скорости:




 , при
, при 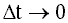 , по вектору
, по вектору  :
: .
. .
. .
. .
. .
. определить закон движения тела (м.т.).
определить закон движения тела (м.т.).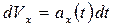 находится скорость как функция времени:
находится скорость как функция времени:  . (V 0 – константа интегрирования).
. (V 0 – константа интегрирования). находится координата как функция времени:
находится координата как функция времени:  . (x 0 – константа интегрирования).
. (x 0 – константа интегрирования). , получаем закон равнопеременного движения:
, получаем закон равнопеременного движения: 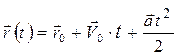 – квадратичная зависимость радиуса вектора от времени и линейная зависимость скорости от времени
– квадратичная зависимость радиуса вектора от времени и линейная зависимость скорости от времени  .
.


