
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении количества движения материальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Теорема в дифференциальной форме. Производная по времени от количества движения материальной точки равна геометрической сумме сил, действующих на точку. Доказательство. Запишем основной закон динамики в виде
2. Теорема в интегральной (конечной) форме. Изменение количества движения материальной точки за некоторый промежуток времени равно геометрической сумме импульсов сил, действующих на точку, за тот же промежуток времени. Доказательство.
Векторные равенства (3.17) и (3.18) можно записать в проекциях на оси декартовых координат:
Прирешении задач уравнения (3.19) следует применять в тех случаях, когда на точку кроме постоянных сил действуют переменные силы, зависящие от скорости точки.
Решение. Применим теорему об изменении материальной точки в дифференциальной форме в проекции на ось
Уравнения (3.20) позволяют косвенным путем определить импульс сил, не зная ни сил, ни времени их действия, если при этом начальная и конечная скорости точки известны. Пример 5.
Импульс сил Теорема об изменении главного вектора количества движения механической системы 1. Теорема в дифференциальной форме Производная по времени от главного вектора количеств движения механической системы равна геометрической сумме внешних сил, действующих на эту систему. Доказательство. На любую Для всей системы
где В проекциях на оси декартовых координат (3.21) имеет вид
Следствия из теоремы: 1. Если 2. Если проекция главного вектора на какую-либо ось равна нулю, то проекция количества движения на эту ось есть величина постоянная. Например,
2. Теорема в интегральной (конечной) форме. Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов всех внешних сил, действующих на точки механической системы, за тот же промежуток времени. Доказательство.
где Векторному равенству (3.23) соответствуют три равенства в скалярной форме
Следствия из теоремы. 1. Если 2. Если
Решение. Внешними силами являются вес лодки
3.6. Момент количества движения материальной точки относительно центра и оси 1. Алгебраический момент количества движения относительно центра.
Правило знаков: Алгебраический момент количества движения материальной точки относительно некоторого центра
 — вектор, приложенный в этом центре и направленный перпендикулярно плоскости векторов — вектор, приложенный в этом центре и направленный перпендикулярно плоскости векторов  и и  в ту сторону, откуда движение точки видно против хода часовой стрелки. в ту сторону, откуда движение точки видно против хода часовой стрелки.
Это определение удовлетворяет векторному равенству
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.148 (0.007 с.) |

 ,
,  ;
; (3.17)
(3.17)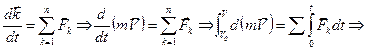
 (3.18)
(3.18) ,
,  ,
,  (3.19)
(3.19) ,
, 
 (3.20)
(3.20) Пример 4.
Пример 4. Точка массы
Точка массы 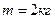 движется горизонтально под действием силы
движется горизонтально под действием силы  в среде, сопротивление которой определяется силой
в среде, сопротивление которой определяется силой  , где
, где 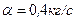 . Какую скорость приобретет точка за время
. Какую скорость приобретет точка за время  , если движение началось без начальной скорости?
, если движение началось без начальной скорости? . Покажем силы
. Покажем силы 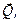

 и
и  (рис. 6).
(рис. 6). ;
; 
 . Ответ.
. Ответ. 
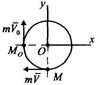
 Материальная точка массы
Материальная точка массы 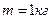 движется по окружности с постоянной скоростью
движется по окружности с постоянной скоростью  из точки
из точки  (рис. 7, а). Определить импульс сил, действующих на точку, за время, в течение которого точка пройдет — длины окружности.
(рис. 7, а). Определить импульс сил, действующих на точку, за время, в течение которого точка пройдет — длины окружности. Решение. Применим теорему об изменении количества движения материальной точки в интегральной форме
Решение. Применим теорему об изменении количества движения материальной точки в интегральной форме  . Найдем проекции импульса
. Найдем проекции импульса  на оси координат
на оси координат  (рис. 7, б):
(рис. 7, б): ;
;  .
. . Ответ.
. Ответ.  .
.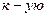 точку механической системы действуют силы
точку механической системы действуют силы 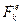 и
и  . Для этой точки в соответствии с (3.17)
. Для этой точки в соответствии с (3.17) 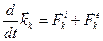 .
. , (3.21)
, (3.21)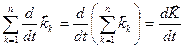 ;
;  .
. ;
;  ,
,  . (3.22)
. (3.22)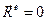 , то
, то  .
. , то
, то  .
. (3.23)
(3.23) — импульс главного вектора внешних сил.
— импульс главного вектора внешних сил. ,
,  ,
,  (3.24)
(3.24) , то
, то 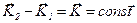 .
.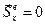 , то
, то 
 Пример 6.
Пример 6. Лодка массы
Лодка массы  , на корме которой стоял человек массы
, на корме которой стоял человек массы  , двигалась соскоростью
, двигалась соскоростью  . Затем человек спрыгнул с лодки со скоростью
. Затем человек спрыгнул с лодки со скоростью  против ее движения. С какой скоростью
против ее движения. С какой скоростью  после этого будет двигаться лодка?
после этого будет двигаться лодка? , вес человека
, вес человека  , (рис. 8). Силой сопротивления движению пренебрегаем. Все силы перпендикулярны оси
, (рис. 8). Силой сопротивления движению пренебрегаем. Все силы перпендикулярны оси  .
. 
 . Ответ.
. Ответ. 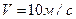
 ,
, 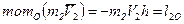 .
.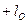 — при движении точки против хода часовой стрелки;
— при движении точки против хода часовой стрелки; 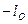 — то же по ходу часовой стрелки.
— то же по ходу часовой стрелки. или
или  и равная произведению модуля количества движения
и равная произведению модуля количества движения  (перпендикуляр) от этого центра до линии, вдоль которой направлен вектор
(перпендикуляр) от этого центра до линии, вдоль которой направлен вектор  (3.25)
(3.25) 2. Векторный момент количества движения относительно центра (рис. 9).
2. Векторный момент количества движения относительно центра (рис. 9).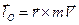 (3.26)
(3.26)


