
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении момента количества движения материальной точки относительно центра и осиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Теорема моментов относительно центра. Производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна моменту силы, действующей на точку, относительно того же центра.
 , , 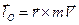 , ,  . . 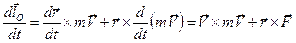 . .  . .  — момент силы — момент силы  относительно точки относительно точки  . Итак, . Итак,  (3.32) (3.32)
Следствие. Если линия действия равнодействующей приложенных к точке сил все время проходит через неподвижный центр, то момент количества движения материальной точки относительно этого центра остается постоянным.
2. Теорема моментов относительно оси. Производная по времени от момента количества движения материальной точки относительно некоторой оси равна моменту силы, действующей на точку, относительно той же оси. Доказательство. Запишем (3.32) в проекциях на оси декартовых координат, учитывая, что где Следствие. Если момент равнодействующей сил, действующих на материальную точку, относительно некоторой оси равен нулю, то момент количества движения материальной точки относительно той же оси остается величиной постоянной.
Решение. На гирьку (рис. 17, б) действуют силы: натяжение
Ответ. Теорема об изменении кинетического момента механической системы относительно центра и оси 1. Теорема моментов относительно центра. Производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра равна геометрической сумме моментов всех внешних сил, действующих на систему, относительно того же центра. Доказательство. Для
Следствие. Если главный момент внешних сил относительно некоторого центра равен нулю, то кинетический момент системы относительно этого центра не изменяется (закон сохранения кинетического момента). 2. Теорема моментов относительно оси. Производная по времени от кинетического момента механической системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил, действующих на систему, относительно этой оси. Доказательство. Спроектируем векторное равенство (3.34) на оси декартовых координат, получим
где Следствие. Если главный момент внешних сил относительно некоторой оси равен нулю, то кинетический момент системы относительно этой оси не изменяется.
Пример 9. Используя условие примера 7, определить угловую скорость вращения конуса в момент, когда материальная точка будет находиться на основании конуса, если в начальный момент она находилась в вершине конуса, а его угловая скорость
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 596; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.32.186 (0.01 с.) |

 Доказательство (рис. 15).
Доказательство (рис. 15).
 Примечание: Такая сила называется центральной. Например, рассмотрим движение спутника вокруг Земли (рис. 16).
Примечание: Такая сила называется центральной. Например, рассмотрим движение спутника вокруг Земли (рис. 16).  , то
, то 
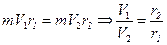 — обратная зависимость между скоростями и расстояниями.
— обратная зависимость между скоростями и расстояниями.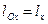 ,
,  ,
,  и
и  ,
,  ,
,  . Тогда
. Тогда  ,
,  ,
,  (3.33)
(3.33) ,
,  ,
,  — моменты количества движения материальной точки относительно осей координат;
— моменты количества движения материальной точки относительно осей координат;  ,
,  , — моменты силы относительно тех же осей.
, — моменты силы относительно тех же осей.
 Пример 8.
Пример 8. К концу нити привязана тяжелая гирька. Второй конец нити переброшен через неподвижный блок. Когда нить с грузом отклонили от вертикали на некоторый угол и сообщили ему вокруг вертикальной оси скорость
К концу нити привязана тяжелая гирька. Второй конец нити переброшен через неподвижный блок. Когда нить с грузом отклонили от вертикали на некоторый угол и сообщили ему вокруг вертикальной оси скорость  , направленную по касательной к траектории, нить начали укорачивать со скоростью
, направленную по касательной к траектории, нить начали укорачивать со скоростью  . Определить, с какой скоростью будет двигаться гирька вокруг оси
. Определить, с какой скоростью будет двигаться гирька вокруг оси  , когда расстояние до оси уменьшится в 2 раза (рис. 17, а).
, когда расстояние до оси уменьшится в 2 раза (рис. 17, а). нити и вес
нити и вес  гирьки. Применим теорему об изменении момента количества движения материальной точки относительно оси
гирьки. Применим теорему об изменении момента количества движения материальной точки относительно оси 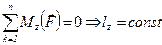 . Вектор
. Вектор  пересекает ось
пересекает ось  .
. .
. точки системы
точки системы  . Выполняя суммирование по всем точкам системы, получим
. Выполняя суммирование по всем точкам системы, получим  , где
, где  ;
;  — главный момент внешних сил относительно центра
— главный момент внешних сил относительно центра  — по свойству внутренних сил.
— по свойству внутренних сил. (3.34)
(3.34) ,
,  ,
,  (3.35)
(3.35) ,
,  ,
,  — кинетические моменты механической системы относительно осей координат;
— кинетические моменты механической системы относительно осей координат;  ,
,  ,
,  — главные моменты внешних сил относительно осей координат.
— главные моменты внешних сил относительно осей координат.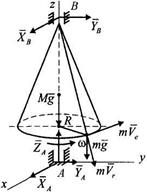 Например,
Например,  , тогда
, тогда 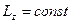 .
. . Масса точки
. Масса точки 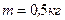 , масса конуса
, масса конуса  .
. Решение. Внешними силами, действующими на механическую систему (конус + материальная точка), являются силы тяжести
Решение. Внешними силами, действующими на механическую систему (конус + материальная точка), являются силы тяжести  конуса и
конуса и 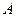 —
— 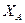 ,
,  ,
,  и подшипника
и подшипника  —
—  и
и 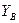 (рис.18). Применим теорему об изменении кинетического момента относительно оси
(рис.18). Применим теорему об изменении кинетического момента относительно оси  . Так как внешние силы либо параллельны оси
. Так как внешние силы либо параллельны оси  , т. е.
, т. е.  .
.  — кинетический момент конуса.
— кинетический момент конуса. 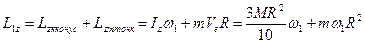 . Тогда
. Тогда 
 . Ответ.
. Ответ. 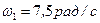 .
.


