
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И механической системы (часть 1)Содержание книги Поиск на нашем сайте
РАЗДЕЛ 3. ДИНАМИКА. ТЕМА 3. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ (часть 1) Теорема о движении центра масс системы Теорема. Центр масс механической системы движется как любая материальная точка, масса которой равна массе всей механической системы и к которой приложена сила, равная главному вектору внешних сил. Доказательство. Основное уравнение динамики для
где
С учетом этого (3.1) примет вид
Уравнение (3.2) может быть записано в скалярной форме в проекциях на оси декартовых координат или на естественные оси. В декартовых осях (3.2) имеет вид
Следствия из теоремы: 1. Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс механической системы движется равномерно и прямолинейно либо покоится. 2. Если проекция главного вектора внешних сил, действующих на систему, на какую-либо ось равна нулю, то проекция центра масс на эту ось либо покоится, либо движется равномерно, т. е., например, если Если в начальный момент система покоилась, то Эти следствия выражают закон сохранения движения центра масс механической системы. При
где Пример 1.
Теорема о движении центра масс Ответ: призма переместится влево на Количество движения материальной точки и механической системы Количество движения материальной точки — векторная мера ее движения, равная произведению массы точки на вектор ее скорости:
Количество движения механической системы или главный вектор количества движения — геометрическая сумма количеств движения всех материальных точек системы:
Преобразуем (3.6):
где Если механическая система состоит из твердых тел, то по формуле (3.7) определяется количество движения каждого
где Модуль главного вектора количества движения системы определяется через его проекции на оси декартовых координат
Например, определить количество движения системы:
3. Система из двух ползунов, соединенных невесомым стержнем (рис. 5):
Пусть Из кинематики известно, что…. Тогда Импульс силы Импульс силы — векторнаямера действия силы в течение некоторого времени. Элементарный импульс
Импульс
Выражение (3.11) в проекциях на оси декартовых координат;
Пример 3. На материальную точку действует сила Решение. Проекции силы на оси координат
Модуль импульса силы. Если на точку действует несколько сил, то они заменяются равнодействующей
Действие внешних сил, приложенных к механической системе за некоторый промежуток времени
Векторному равенству (3.14) соответствуют три скалярных
где
Пример 5.
Импульс сил Пример 9. Используя условие примера 7, определить угловую скорость вращения конуса в момент, когда материальная точка будет находиться на основании конуса, если в начальный момент она находилась в вершине конуса, а его угловая скорость
РАЗДЕЛ 3. ДИНАМИКА. ТЕМА 3. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ (часть 1)
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.253.240 (0.009 с.) |

 материальной точки
материальной точки  . Для всей механической системы
. Для всей механической системы , (3.1)
, (3.1) — по свойству внутренних сил;
— по свойству внутренних сил;  — главный вектор всех
— главный вектор всех 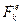 внешних сил, приложенных к системе;
внешних сил, приложенных к системе;
 .
. (3.2)
(3.2) ,
,  ,
,  ,
,  . (3.3)
. (3.3) , то
, то 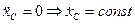 .
. — проекция центра масс покоится. При
— проекция центра масс покоится. При  центр масс будет двигаться вдоль оси
центр масс будет двигаться вдоль оси  с постоянной скоростью.
с постоянной скоростью. справедливо равенство
справедливо равенство , (4.3)
, (4.3) — приращение координаты центра масс
— приращение координаты центра масс  тела при изменении положения тел в механической системе, равное проекции абсолютного перемещения этой точки на ось
тела при изменении положения тел в механической системе, равное проекции абсолютного перемещения этой точки на ось 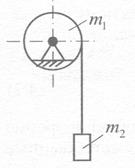
 К концу троса, навитого на барабан, подвешен груз массы
К концу троса, навитого на барабан, подвешен груз массы  . Барабан массы
. Барабан массы 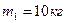 может вращаться вокруг горизонтальной оси. Определить реакцию оси, если груз начнет двигаться с постоянным ускорением
может вращаться вокруг горизонтальной оси. Определить реакцию оси, если груз начнет двигаться с постоянным ускорением  (рис. 1, а).
(рис. 1, а). Решение. Покажем внешние силы — вес барабана
Решение. Покажем внешние силы — вес барабана  , вес груза
, вес груза  ,реакцию
,реакцию 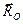 оси
оси  (рис. 1, б). Запишем теорему о движении центра масс механической системы:
(рис. 1, б). Запишем теорему о движении центра масс механической системы:  . Выберем начало оси
. Выберем начало оси  . Отсюда
. Отсюда  . Запишем координату центра масс:
. Запишем координату центра масс: 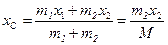 , т.к.
, т.к. 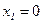 , а
, а  . Продифференцируем дважды, определим ускорение центра масс:
. Продифференцируем дважды, определим ускорение центра масс:  . Тогда
. Тогда  . Ответ.
. Ответ. 
 Пример 2.
Пример 2. Призма
Призма 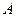 массы
массы  покоится на гладкой горизонтальной плоскости. По наклонной плоскости призмы из состояния покоя начинает перемещаться груз
покоится на гладкой горизонтальной плоскости. По наклонной плоскости призмы из состояния покоя начинает перемещаться груз  массы
массы  . Пренебрегая размерами груза, определить перемещение призмы, когда он переместится на расстояние
. Пренебрегая размерами груза, определить перемещение призмы, когда он переместится на расстояние  ;
;  (рис. 2, а).
(рис. 2, а). Решение. Внешние силы, действующие на систему: вес
Решение. Внешние силы, действующие на систему: вес  плоскости (рис. 2, б).
плоскости (рис. 2, б). . Так как
. Так как  (все силы перпендикулярны оси
(все силы перпендикулярны оси  , где
, где  .
.  .
.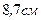 .
. (3.5)
(3.5) (3.6)
(3.6)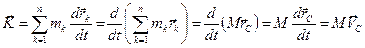 (3.7)
(3.7) — скорость центра масс.
— скорость центра масс. тела, а затем
тела, а затем (3.8)
(3.8)
 — скорость центра масс
— скорость центра масс 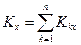 ,
,  ,
,  ,
,  (3.9)
(3.9)
 1. Вращение тела вокруг неподвижной оси, проходящей через центр масс (рис. 3). Так как
1. Вращение тела вокруг неподвижной оси, проходящей через центр масс (рис. 3). Так как  , то
, то  .
.

 2. Качение тела по плоскости — плоскопараллельное движение — поступательное вместе с центром масс,
2. Качение тела по плоскости — плоскопараллельное движение — поступательное вместе с центром масс,  и вращательное относительно оси, проходящей через центр масс —
и вращательное относительно оси, проходящей через центр масс —  (рис. 4). Итак,
(рис. 4). Итак,  .
.
 ,
,  ,
,  ,
,  .
. ;
; 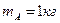 ,
,  .
. .
.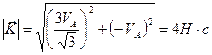 .
. силы — векторная величина, равная произведению вектора силы на элементарный промежуток времени
силы — векторная величина, равная произведению вектора силы на элементарный промежуток времени  , т. е,
, т. е, (3.10)
(3.10) силы
силы  за конечный промежуток времени
за конечный промежуток времени  равен интегральной сумме соответствующих элементарных импульсов, т. е.
равен интегральной сумме соответствующих элементарных импульсов, т. е. (3.11)
(3.11) ,
,  ,
,  ,
,  (3.12)
(3.12) . Определить импульс силы за время
. Определить импульс силы за время  .
. ,
,  Fy = 6;
Fy = 6; 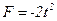 . Проекции импульса силы на оси
. Проекции импульса силы на оси  ,
,  ,
, 
 . Ответ.
. Ответ. 
 , импульс которой
, импульс которой 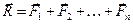 .
. . (3.13)
. (3.13) , характеризуется импульсом главного вектора
, характеризуется импульсом главного вектора  внешних сил:
внешних сил: . (3.14)
. (3.14) ,
,  ,
,  (3.15)
(3.15) Rx и т. д. — проекции главного вектора на оси координат. Модуль импульса внешних сил
Rx и т. д. — проекции главного вектора на оси координат. Модуль импульса внешних сил . (3.16)
. (3.16)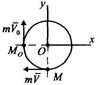
 Материальная точка массы
Материальная точка массы 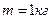 движется по окружности с постоянной скоростью
движется по окружности с постоянной скоростью  из точки
из точки  (рис. 7, а). Определить импульс сил, действующих на точку, за время, в течение которого точка пройдет — длины окружности.
(рис. 7, а). Определить импульс сил, действующих на точку, за время, в течение которого точка пройдет — длины окружности. Решение. Применим теорему об изменении количества движения материальной точки в интегральной форме
Решение. Применим теорему об изменении количества движения материальной точки в интегральной форме  . Найдем проекции импульса
. Найдем проекции импульса  (рис. 7, б):
(рис. 7, б): ;
;  .
. . Ответ.
. Ответ.  .
. . Масса точки
. Масса точки 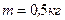 , масса конуса
, масса конуса  .
. Решение. Внешними силами, действующими на механическую систему (конус + материальная точка), являются силы тяжести
Решение. Внешними силами, действующими на механическую систему (конус + материальная точка), являются силы тяжести  конуса и
конуса и  точки, реакции подпятника
точки, реакции подпятника 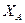 ,
,  ,
,  и подшипника
и подшипника  и
и 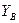 (рис.18). Применим теорему об изменении кинетического момента относительно оси
(рис.18). Применим теорему об изменении кинетического момента относительно оси  :
:  . Так как внешние силы либо параллельны оси
. Так как внешние силы либо параллельны оси  , т. е.
, т. е.  .
.  — кинетический момент конуса.
— кинетический момент конуса. 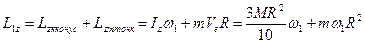 . Тогда
. Тогда 
 . Ответ.
. Ответ. 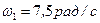 .
.


