
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи движения материальной точки. Кинематические графики движения материальной точки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Равномерное прямолинейное движение - это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, т. е. это движение с постоянной по модулю и направлению скоростью:
2. Равноускоренное прямолинейное движение - это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.
3. Равномерным называется такое криволинейное движение точки, в котором численная величина скорости все время остается постоянной: v=const. Тогда 4. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: aτ=const. Простейшие движения твердого тела. Поступательное движение. Поступательным называется такое движение твердого тела, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе. Траектории точек твердого тела могут быть любыми кривыми линиями. Следовательно | Взяв производные от скоростей обеих точек, Простейшие движения твердого тела. Вращательное движение. Скорости и ускорения различных точек вращающего тела.
Размерность [
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1744; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.162 (0.007 с.) |

 — уравнение скорости,
— уравнение скорости,  — уравнение ускорения.
— уравнение ускорения. =сonst — уравнение ускорения. По определению ускорения
=сonst — уравнение ускорения. По определению ускорения  .
. и все ускорение точки равно одному только нормальному:
и все ускорение точки равно одному только нормальному: 
 и
и 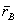 соответственно, а положение точки В относительно точки А - радиусом-вектором
соответственно, а положение точки В относительно точки А - радиусом-вектором  . Тогда
. Тогда  , где
, где  и
и  тогда
тогда  , но
, но 
 |=|
|=|  |
| или |
или |  |=|
|=|  |
|  Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения (коленчатый вал поршневого двигателя, центробежный компрессор, газовая турбина реактивного двигателя, винт самолета вращаются вокруг неподвижных осей). Угол, отсчитываемый от неподвижной полуплоскости против движения часовой стрелки, измеряемый в радианах, называется углом поворота тела -
Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения (коленчатый вал поршневого двигателя, центробежный компрессор, газовая турбина реактивного двигателя, винт самолета вращаются вокруг неподвижных осей). Угол, отсчитываемый от неподвижной полуплоскости против движения часовой стрелки, измеряемый в радианах, называется углом поворота тела - 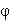 . Уравнение вращения тела вокруг неподвижной оси выражает зависимость угла поворота от времени:
. Уравнение вращения тела вокруг неподвижной оси выражает зависимость угла поворота от времени: Основными характеристиками вращательного движения тела являются угловая скорость -
Основными характеристиками вращательного движения тела являются угловая скорость - 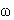 и угловое ускорение -
и угловое ускорение -  .
. ].
].  , численная величина которого равна
, численная величина которого равна  и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Такой вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. В технике угловую скорость часто выражают не в радианах в секунду, а частотой вращения n, выраженной числом оборотов в минуту. Зависимость между n и
и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Такой вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. В технике угловую скорость часто выражают не в радианах в секунду, а частотой вращения n, выраженной числом оборотов в минуту. Зависимость между n и  рад, имеет вид:
рад, имеет вид: Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора
Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора 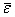 , направленного вдоль оси вращения. При этом направление
, направленного вдоль оси вращения. При этом направление 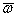 , когда тело вращается ускоренно и противоположно
, когда тело вращается ускоренно и противоположно 
 Величины
Величины 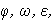 n являются угловыми характеристиками, применимы-ми для всего тела в целом. Их нельзя относить к отдельной точке вращающегося тела или к другой какой-либо точке. Движение точки характеризуется линейными величинами: скоростью
n являются угловыми характеристиками, применимы-ми для всего тела в целом. Их нельзя относить к отдельной точке вращающегося тела или к другой какой-либо точке. Движение точки характеризуется линейными величинами: скоростью  и ускорением
и ускорением  .
.


