
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр параллельных сил. Сила тяжести, центр тяжести тела. Координаты центра тяжести плоской фигуры. Центры тяжести простых геометрических фигур и фигур, имеющих ось симметрии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где xk, yk, zk — координаты точек приложения сил. Понятием Ц. п. с. пользуются при отыскании координат центров тяжести Сила тяжести — сила, действующая на любое материальное тело, находящееся вблизи поверхности Земли или другого астрономического тела. Сила тяжести, действующая на тело, находящееся на поверхности Земли равна массе тела, умноженной на постоянную g=9.8 м/с2.
Ускорение силы тяжести зависит: 1. Массы планеты. 2. Радиуса планеты. 3. От высоты над поверхностью планеты. 4. От географической широты (на полюсах - 9,83 м/с2. на экваторе -9,79 м/с2. 5. От залежей полезных ископаемых. Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела.
Координаты центра тяжести некоторых однородных тел
Симметрия. Если тело имеет центр симметрии, то центр тяжести находится в центре симметрии. Основные понятия кинематики. Покой, равновесие, движение, траектория, путь, скорость, ускорение. Раздел механики, занимающийся изучением движения материальных тел без учета их масс и действующих на них сил, называется кинематикой. Движение - основная форма существования всего материального мира, покой и равновесие - частные случаи. Всякое движение, и механическое в том числе, происходит в пространстве и во времени. Все тела состоят из материальных точек. Чтобы получить правильное представление о движении тел, начинать изучение нужно с движения точки. Перемещение точки в пространстве выражается в метрах, а также в дольных (см, мм) или кратных (км) единицах длины, время - в секундах. В практике или жизненных ситуациях время часто выражают в минутах или часах. Отсчет времени при рассмотрении того или иного движения точки ведут от определенного, заранее обусловленного начального момента (t = 0). Геометрическое место положений движущейся точки в рассматриваемой системе отсчета называется траекторией. По виду траектории движение точки делится на прямолинейное и криволинейное. Траектория точки может быть определена и задана заранее. Так, например, траектории искусственных спутников Земли и межпланетных станций вычисляют заранее, или если принять движущиеся по городу автобусы за материальные точки, то их траектории (маршруты) также известны. В подобных случаях положение точки в каждый момент времени определяется расстоянием (дуговой координатой) S, т.е. длиной участка траектории, отсчитанной от некоторой ее неподвижной точки, принятой за начало отсчета. Отсчет расстояний от начала траектории можно вести в обе стороны, поэтому отсчет в одну какую-либо сторону условно принимают за положительный, а в противоположную - за отрицательный, т.е. расстояние S - величина алгебраическая. Она может быть положительной (S>0) или отрицательной (S<0). При движении точка за определенный промежуток времени проходит некоторый путь L, который измеряется вдоль траектории в направлении движения.
Векторная величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью.
Отметим, что это векторное равенство характеризует лишь положение
Модуль средней скорости равен частному от деления пройденного пути на время, в течение которого этот путь пройден. Векторная величина, характеризующая быстроту изменения направления и числового значения скорости, называется ускорением.
При равномерном движении по криволинейной траектории точка тоже имеет ускорение, так как и в этом случае изменяется направление скорости.
14. Способы задания движения материальной точки. Существует три способа: естественный, координатный, векторный. Естественный способ задания движения точки. Если кроме траектории, на которой отмечено начало отсчета 0, задана зависимость
Пример:
Координатный способ задания движения точки. Когда траектория точки заранее не известна, положение точки в пространстве определяется тремя координатами: абсциссой X, ординатой У и аппликатой Z.
или Эти уравнения выражают закон движения точки в прямоугольной системе координат (OXYZ). В частном случае, если точка движется в плоскости, закон движения точки выражается двумя уравнениями:
Например. Движение точки в плоской системе координат задано уравнениями X = 2t и У=3t (X и У - см, t - с). Тогда в момент времени
Зная закон движения точки в прямоугольной системе координат, можно определить уравнение траектории точки. Например, исключив время t из заданных выше уравнений X = 2t и У = 3t,, получим уравнение траектории ЗХ - 2У = 0. Как видим, в этом случае точка движется по прямой, проходящей через начало координат. 15. Определение скорости и ускорения материальной точки при естественном способе задания ее движения. Естественные оси (касательная, главная нормаль, бинормаль) − это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их положение определяется траекторией движения. Касательная (с единичным вектором Из определения скорости точки
,где,
Тогда 16. Определение скорости и ускорения материальной точки при еоординатном способе задания ее движения. Связь векторного способа задания движения и координатного дается соотношением Из определения скорости:
Проекции скорости на оси координат равны производным соответствующих координат по времени Модуль и направление скорости определяются выражениями:
Точкой сверху здесь и в дальнейшем обозначается дифференцирование по времени Из определения ускорения:
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.31 (0.007 с.) |

 Центр параллельных сил - точка, через которую проходит линия действия равнодействующей системы параллельных сил Fk при любом повороте всех этих сил около их точекприложения в одну и ту же сторону и на один и тот же угол. Координаты Ц. п. с. определяются формулами:
Центр параллельных сил - точка, через которую проходит линия действия равнодействующей системы параллельных сил Fk при любом повороте всех этих сил около их точекприложения в одну и ту же сторону и на один и тот же угол. Координаты Ц. п. с. определяются формулами: - из закона Всемирного тяготения. (где M - масса планеты, m - масса тела, R - расстояние до центра планеты).
- из закона Всемирного тяготения. (где M - масса планеты, m - масса тела, R - расстояние до центра планеты). - сила тяжести из второго закона Ньютона (где m - масса тела, g - ускорение силы тяжести).
- сила тяжести из второго закона Ньютона (где m - масса тела, g - ускорение силы тяжести).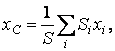 Координаты центра тяжести плоской фигуры определяются по формулам
Координаты центра тяжести плоской фигуры определяются по формулам где
где  – координаты центра тяжести простейшей части фигуры,
– координаты центра тяжести простейшей части фигуры,  – её площадь,
– её площадь,  – суммарная площадь.
– суммарная площадь. где α – половина центрального угла; R – радиус окружности.
где α – половина центрального угла; R – радиус окружности.

 где α – половина центрального угла; R – радиус окружности.
где α – половина центрального угла; R – радиус окружности.

 где α – половина центрального угла; R – радиус окружности.
где α – половина центрального угла; R – радиус окружности.



 где x1, y1, x2, y2, x3, y3 – координаты вершин треугольника
где x1, y1, x2, y2, x3, y3 – координаты вершин треугольника




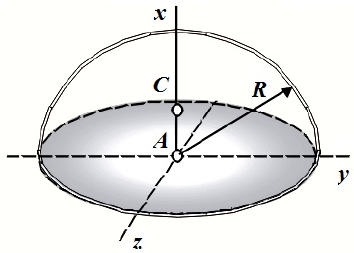

 - площадь фигуры.
- площадь фигуры.

 Если точка стала двигаться не из начала отсчета 0, а из положения, находящегося на начальном расстоянии So то
Если точка стала двигаться не из начала отсчета 0, а из положения, находящегося на начальном расстоянии So то Скорость точки в любой момент ее движения направлена по касательной к траектории.
Скорость точки в любой момент ее движения направлена по касательной к траектории.
 , а модуль средней скорости за время
, а модуль средней скорости за время 
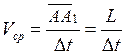 где
где  - путь, пройденный точкой за время
- путь, пройденный точкой за время 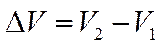

 За единицу ускорения принимают обычно
За единицу ускорения принимают обычно 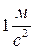 .
. между расстоянием S и временем t, это уравнение называется законом движения точки по заданной траектории.
между расстоянием S и временем t, это уравнение называется законом движения точки по заданной траектории. Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением
Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением 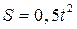
 . Тогда в момент времени
. Тогда в момент времени 
 , т.е. точка находится в начале отсчета 0; в момент времени
, т.е. точка находится в начале отсчета 0; в момент времени 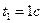 точка находится на расстоянии
точка находится на расстоянии  ; в момент времени
; в момент времени точка находится на расстоянии
точка находится на расстоянии 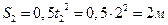 от начала отсчета 0.
от начала отсчета 0.

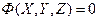 , исключив время.
, исключив время. или
или  .
. и уо = 0, т.е. точка находится в начале координат; в момент времени
и уо = 0, т.е. точка находится в начале координат; в момент времени  ,
,  ; в момент времени
; в момент времени  ,
, и т.д.
и т.д. ) направлена по касательной в положительном направлении отсчета дуговой координаты и находится как предельное положение секущей, проходящей через данную точку. Через касательную проходит соприкасающаяся плоскость, которая находится как предельное положение плоскости p при стремлении точки M1 к точке M. Нормальная плоскость перпендикулярна касательной. Линия пересечения нормальной и соприкасающейся плоскостей − главная нормаль. Единичный вектор главной нормали
) направлена по касательной в положительном направлении отсчета дуговой координаты и находится как предельное положение секущей, проходящей через данную точку. Через касательную проходит соприкасающаяся плоскость, которая находится как предельное положение плоскости p при стремлении точки M1 к точке M. Нормальная плоскость перпендикулярна касательной. Линия пересечения нормальной и соприкасающейся плоскостей − главная нормаль. Единичный вектор главной нормали  направлен в сторону вогнутости траектории. Бинормаль (с единичным вектором
направлен в сторону вогнутости траектории. Бинормаль (с единичным вектором  ) направлена перпендикулярно касательной и главной нормали так, что орты
) направлена перпендикулярно касательной и главной нормали так, что орты  ,
,  и
и  образуют правую тройку векторов. Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник, который перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.
образуют правую тройку векторов. Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник, который перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.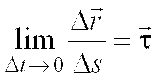

 − единичный вектор касательной.
− единичный вектор касательной. ,
, 
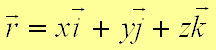
 .
. ,
, 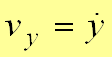 ,
,  ..
.. ,
,

 .
. .
.


