
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Свободное опирание тела о связь.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные положения статики. Основные понятия статики: материальная точка, абсолютно твердое тело, система сил. Материальной точкой называют геометрическую точку, обладающую массой. Абсолютно твердым телом называют такое материальное тело, в котором расстояние между любыми двумя точками всегда остается неизменным. Способность тел сопротивляться изменению их формы и размеров называется жесткостью. Мера механического действия одного материального тела на другое называется силой. Сила - величина векторная. Она определяется, во-первых, числовым значением (модулем), во-вторых, точкой приложения (местом контакта взаимодействующих тел), в-третьих, направлением действия. В Международной системе единиц (СИ) сила выражается в ньютонах (сокращенное обозначение Н).1Н - небольшая сила, поэтому часто употребляют кратные единицы - килоньютон (1 кН = 103 Н) и меганьютон (1 МН = 106 Н). Как всякий вектор, силу можно изобразить графически в виде направленного отрезка.
Силы, действующие на твердое тело со стороны других тел, называются внешними. Силы, действующие на материальные точки твердого тела со стороны других точек того же тела, называются внутренними. Аксиомы статики. Аксиома 1 (принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные силы не выведут ее из этого состояния. Состояние покоя или равномерного и прямолинейного движения точки называют равновесием. Аксиома 2 (условие равновесия двух сил). Две силы, приложенные к твердому телу, образуют уравновешенную систему только тогда, когда они равны по модулю и действуют вдоль одной прямой в противоположные стороны.
Аксиома 3 (принцип присоединения и исключения уравновешенных сил). Действие данной системы сил на твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Следствие 1. Силу, приложенную к твердому телу, можно переносить вдоль линии ее действия в любую другую точку, действие силы на тело при этом не нарушится. Свойство вектора силы справедливо только в теоретической механике (механике абсолютно твердого тела).
Две силы
Аксиома 6 (принцип отвердевания). Если деформируемое тело находится в равновесии, то равновесие этого тела не нарушится, если, не изменяя формы, размеров, положения в пространстве, оно превратится в абсолютно твердое тело, т.е. затвердеет. 3. Связи и их реакции. Виды связей и правила определения направления реакций связей. Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении. В качестве примера свободного тела приведем летящий воздушный шар или ракету в космосе. Твердое тело называется несвободным, если его перемещение в пространстве ограничено какими-либо другими телами. Все тела, которые, так или иначе ограничивают перемещение данного тела, называются его связями. Задача определения реакций связей - одна из основных задач статики. Некоторые разновидности связей и правила определения их реакций. Основные понятия кинематики. Покой, равновесие, движение, траектория, путь, скорость, ускорение. Раздел механики, занимающийся изучением движения материальных тел без учета их масс и действующих на них сил, называется кинематикой. Движение - основная форма существования всего материального мира, покой и равновесие - частные случаи. Всякое движение, и механическое в том числе, происходит в пространстве и во времени. Все тела состоят из материальных точек. Чтобы получить правильное представление о движении тел, начинать изучение нужно с движения точки. Перемещение точки в пространстве выражается в метрах, а также в дольных (см, мм) или кратных (км) единицах длины, время - в секундах. В практике или жизненных ситуациях время часто выражают в минутах или часах. Отсчет времени при рассмотрении того или иного движения точки ведут от определенного, заранее обусловленного начального момента (t = 0). Геометрическое место положений движущейся точки в рассматриваемой системе отсчета называется траекторией. По виду траектории движение точки делится на прямолинейное и криволинейное. Траектория точки может быть определена и задана заранее. Так, например, траектории искусственных спутников Земли и межпланетных станций вычисляют заранее, или если принять движущиеся по городу автобусы за материальные точки, то их траектории (маршруты) также известны. В подобных случаях положение точки в каждый момент времени определяется расстоянием (дуговой координатой) S, т.е. длиной участка траектории, отсчитанной от некоторой ее неподвижной точки, принятой за начало отсчета. Отсчет расстояний от начала траектории можно вести в обе стороны, поэтому отсчет в одну какую-либо сторону условно принимают за положительный, а в противоположную - за отрицательный, т.е. расстояние S - величина алгебраическая. Она может быть положительной (S>0) или отрицательной (S<0). При движении точка за определенный промежуток времени проходит некоторый путь L, который измеряется вдоль траектории в направлении движения.
Векторная величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью.
Отметим, что это векторное равенство характеризует лишь положение
Модуль средней скорости равен частному от деления пройденного пути на время, в течение которого этот путь пройден. Векторная величина, характеризующая быстроту изменения направления и числового значения скорости, называется ускорением.
При равномерном движении по криволинейной траектории точка тоже имеет ускорение, так как и в этом случае изменяется направление скорости.
14. Способы задания движения материальной точки. Существует три способа: естественный, координатный, векторный. Естественный способ задания движения точки. Если кроме траектории, на которой отмечено начало отсчета 0, задана зависимость
Пример:
Координатный способ задания движения точки. Когда траектория точки заранее не известна, положение точки в пространстве определяется тремя координатами: абсциссой X, ординатой У и аппликатой Z.
или Эти уравнения выражают закон движения точки в прямоугольной системе координат (OXYZ). В частном случае, если точка движется в плоскости, закон движения точки выражается двумя уравнениями:
Например. Движение точки в плоской системе координат задано уравнениями X = 2t и У=3t (X и У - см, t - с). Тогда в момент времени
Зная закон движения точки в прямоугольной системе координат, можно определить уравнение траектории точки. Например, исключив время t из заданных выше уравнений X = 2t и У = 3t,, получим уравнение траектории ЗХ - 2У = 0. Как видим, в этом случае точка движется по прямой, проходящей через начало координат. 15. Определение скорости и ускорения материальной точки при естественном способе задания ее движения. Естественные оси (касательная, главная нормаль, бинормаль) − это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их положение определяется траекторией движения. Касательная (с единичным вектором Из определения скорости точки
,где,
Тогда 16. Определение скорости и ускорения материальной точки при еоординатном способе задания ее движения. Связь векторного способа задания движения и координатного дается соотношением Из определения скорости:
Проекции скорости на оси координат равны производным соответствующих координат по времени Модуль и направление скорости определяются выражениями:
Точкой сверху здесь и в дальнейшем обозначается дифференцирование по времени Из определения ускорения:
Планетарные передачи. Планетарная передача — механическая передача вращательного движения, за счёт своей конструкции способная в пределах одной геометрической оси вращения изменять, складывать и раскладывать подводимые угловые скорости и/или крутящий момент. Обычно является элементом трансмиссии различных технологических и транспортных машин. Конструктивно ПП всегда представляет собой набор взаимозацепленных зубчатых колёс (как минимум, не менее 4-х), часть из которых (не менее 2-х) имеет общую геометрическую неподвижную ось вращения, а другая часть (также, не менее 2-х) имеет подвижные оси вращения, концентрически вращающиеся на так называемом «водиле» вокруг неподвижной. Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую, а через зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться относительно первых, но и обкатывать их, тем самым передавая поступательное движение на водило, все звенья ПП на которые можно подавать/снимать мощность получают возможность вращаться дифференциально, с тем лишь условием, что угловая скорость любого такого звена не абсолютно хаотична, а определяется угловыми скоростями всех остальных звеньев. В этом плане ПП похожа на планетарную систему, в которой скорость каждой планеты определяется скоростями всех остальных планет системы. Дифференциальный принцип вращения всей системы, а также то, что в своём каноническом виде набор зубчатых колёс, составляющих ПП, собран в некоем подобии солнца и эпициклически движущихся по орбите планет, даёт данной механической передаче такие присущие только ей интернациональные определения, как планетарная, дифференциальная или эпициклическая, каждое из которых в данном случае есть синонимы. С точки зрения теоретической механики планетарная передача — это механическая система с двумя и более степенями свободы. Эта особенность, являющаяся прямым следствием конструкции, есть важное отличие ПП от каких-либо других передач вращательного движения, всегда имеющих только одну степень свободы. И эта особенность наделяет саму ПП тем важным качеством, что в аспекте воздействия на угловые скорости вращения ПП может не только редуцировать эти скорости, но и складывать и раскладывать их, что, в свою очередь, делает её основным механическим исполнительным узлом не только различных планетарных редукторов, но таких устройств как дифференциалы и суммирующие ПП. Наиболее широкое применение принцип нашёл в планетарных редукторах, автомобильных дифференциалах, бортовых планетарных передачах ведущих мостов тяжёлых автомобилей, кроме того, используется в суммирующих звеньях кинематических схем металлорежущих станков, также в редукторах привода воздушных винтов турбовинтовых двигателей (ТВД) в авиации, также довольно распространены планетарные втулки для велосипедов. В современных устройствах могут использоваться каскады из нескольких планетарных передач для получения большого диапазона передаточных чисел. На этом принципе работают многие автоматические коробки передач. Часто планетарные передачи используются для суммирования двух потоков мощности (например, планетарные ряды двухпоточных трансмиссий некоторых танков и др. гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила. Планетарные передачи также используются в случаях, когда необходимо переменное передаточное отношение (может быть достигнуто торможением, например, водила). Конструкция передачи со многими сателлитами обеспечивает зацепление большего числа зубцов и потому меньшую нагрузку на каждый зубец. Это позволяет достичь меньших размеров и массы по сравнению с обычной передачей при той же передаваемой мощности. Соосность ведущих и ведомых валов облегчает компоновку машин и каскадных механизмов. Сбалансированность сил в передаче приводит к меньшему уровню шума. Конструкция передачи позволяет достичь больших передаточных отношений при малом числе колёс. К недостаткам планетарных передач относят повышенные требования к точности изготовления и сборки, а также малый КПД при больших передаточных отношениях. Основные понятия и аксиомы динамики.
Силы, вызывающие ускорение данного тела, и силы инерции, возникающие вследствие ускорения, всегда равны по величине и противоположно направлены. Fu=-F, F-ma=0, Fu=-ma Здесь: Чтобы установить, как движется тело, на которое действует сразу несколько сил, часто пользуются принципом динамического равновесия (ΣF = 0), причем в этом случае кроме действующих сил и сил трения следует также учитывать кажущиеся силы инерции (принцип Даламбера). Основные положения статики. Основные понятия статики: материальная точка, абсолютно твердое тело, система сил. Материальной точкой называют геометрическую точку, обладающую массой. Абсолютно твердым телом называют такое материальное тело, в котором расстояние между любыми двумя точками всегда остается неизменным. Способность тел сопротивляться изменению их формы и размеров называется жесткостью. Мера механического действия одного материального тела на другое называется силой. Сила - величина векторная. Она определяется, во-первых, числовым значением (модулем), во-вторых, точкой приложения (местом контакта взаимодействующих тел), в-третьих, направлением действия. В Международной системе единиц (СИ) сила выражается в ньютонах (сокращенное обозначение Н).1Н - небольшая сила, поэтому часто употребляют кратные единицы - килоньютон (1 кН = 103 Н) и меганьютон (1 МН = 106 Н). Как всякий вектор, силу можно изобразить графически в виде направленного отрезка.
Силы, действующие на твердое тело со стороны других тел, называются внешними. Силы, действующие на материальные точки твердого тела со стороны других точек того же тела, называются внутренними. Аксиомы статики. Аксиома 1 (принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные силы не выведут ее из этого состояния. Состояние покоя или равномерного и прямолинейного движения точки называют равновесием. Аксиома 2 (условие равновесия двух сил). Две силы, приложенные к твердому телу, образуют уравновешенную систему только тогда, когда они равны по модулю и действуют вдоль одной прямой в противоположные стороны.
Аксиома 3 (принцип присоединения и исключения уравновешенных сил). Действие данной системы сил на твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Следствие 1. Силу, приложенную к твердому телу, можно переносить вдоль линии ее действия в любую другую точку, действие силы на тело при этом не нарушится. Свойство вектора силы справедливо только в теоретической механике (механике абсолютно твердого тела).
Две силы
Аксиома 6 (принцип отвердевания). Если деформируемое тело находится в равновесии, то равновесие этого тела не нарушится, если, не изменяя формы, размеров, положения в пространстве, оно превратится в абсолютно твердое тело, т.е. затвердеет. 3. Связи и их реакции. Виды связей и правила определения направления реакций связей. Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении. В качестве примера свободного тела приведем летящий воздушный шар или ракету в космосе. Твердое тело называется несвободным, если его перемещение в пространстве ограничено какими-либо другими телами. Все тела, которые, так или иначе ограничивают перемещение данного тела, называются его связями. Задача определения реакций связей - одна из основных задач статики. Некоторые разновидности связей и правила определения их реакций. I. Свободное опирание тела о связь. Тело изображено в виде бруска, а связь заштрихована.
3. Стержневая связь. Реакции стержневых связей направлены вдоль прямой, проходящей через оси концевых шарниров.
4. Шарнирно-подвижная опора представляет собой видоизменение свободного опирания.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.44.171 (0.014 с.) |

 Сила тяжести всегда направлена вертикально вниз.
Сила тяжести всегда направлена вертикально вниз. Несколько сил, действующих на какое-либо одно твердое тело, называется системой сил.
Несколько сил, действующих на какое-либо одно твердое тело, называется системой сил.

 Аксиома 4 (правило параллелограмма). Две приложенные к точке тела силы имеют равнодействующую, приложенную в той же точке и равную диагонали параллелограмма, построенного на этих силах, как на сторонах.
Аксиома 4 (правило параллелограмма). Две приложенные к точке тела силы имеют равнодействующую, приложенную в той же точке и равную диагонали параллелограмма, построенного на этих силах, как на сторонах. и
и  приложены к разным точкам тела, но линии их действия лежат в одной плоскости.
приложены к разным точкам тела, но линии их действия лежат в одной плоскости.
 Аксиома 5 (закон действия и противодействия). Силы взаимодействия двух твердых тел друг на друга равны по модулю и направлены по одной прямой в противоположные стороны.
Аксиома 5 (закон действия и противодействия). Силы взаимодействия двух твердых тел друг на друга равны по модулю и направлены по одной прямой в противоположные стороны.
 Если точка стала двигаться не из начала отсчета 0, а из положения, находящегося на начальном расстоянии So то
Если точка стала двигаться не из начала отсчета 0, а из положения, находящегося на начальном расстоянии So то Скорость точки в любой момент ее движения направлена по касательной к траектории.
Скорость точки в любой момент ее движения направлена по касательной к траектории.
 , а модуль средней скорости за время
, а модуль средней скорости за время 
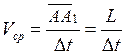 где
где  - путь, пройденный точкой за время
- путь, пройденный точкой за время 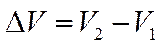

 За единицу ускорения принимают обычно
За единицу ускорения принимают обычно 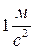 .
. между расстоянием S и временем t, это уравнение называется законом движения точки по заданной траектории.
между расстоянием S и временем t, это уравнение называется законом движения точки по заданной траектории. Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением
Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением 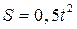
 . Тогда в момент времени
. Тогда в момент времени 
 , т.е. точка находится в начале отсчета 0; в момент времени
, т.е. точка находится в начале отсчета 0; в момент времени 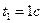 точка находится на расстоянии
точка находится на расстоянии  ; в момент времени
; в момент времени точка находится на расстоянии
точка находится на расстоянии 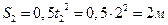 от начала отсчета 0.
от начала отсчета 0.

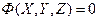 , исключив время.
, исключив время. или
или  .
. и уо = 0, т.е. точка находится в начале координат; в момент времени
и уо = 0, т.е. точка находится в начале координат; в момент времени  ,
,  ; в момент времени
; в момент времени  ,
, и т.д.
и т.д.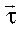 ) направлена по касательной в положительном направлении отсчета дуговой координаты и находится как предельное положение секущей, проходящей через данную точку. Через касательную проходит соприкасающаяся плоскость, которая находится как предельное положение плоскости p при стремлении точки M1 к точке M. Нормальная плоскость перпендикулярна касательной. Линия пересечения нормальной и соприкасающейся плоскостей − главная нормаль. Единичный вектор главной нормали
) направлена по касательной в положительном направлении отсчета дуговой координаты и находится как предельное положение секущей, проходящей через данную точку. Через касательную проходит соприкасающаяся плоскость, которая находится как предельное положение плоскости p при стремлении точки M1 к точке M. Нормальная плоскость перпендикулярна касательной. Линия пересечения нормальной и соприкасающейся плоскостей − главная нормаль. Единичный вектор главной нормали  направлен в сторону вогнутости траектории. Бинормаль (с единичным вектором
направлен в сторону вогнутости траектории. Бинормаль (с единичным вектором  ) направлена перпендикулярно касательной и главной нормали так, что орты
) направлена перпендикулярно касательной и главной нормали так, что орты  ,
, 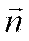 и
и  образуют правую тройку векторов. Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник, который перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.
образуют правую тройку векторов. Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник, который перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.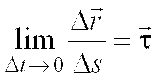

 − единичный вектор касательной.
− единичный вектор касательной. ,
, 
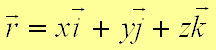
 .
. ,
, 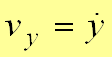 ,
,  ..
.. ,
,

 .
. .
. называют основным уравнением динамики точки
Третья аксиома (закон равенства действия и противодействия). Две материальных точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, (проходящей через эти точки), в противоположные стороны.
Четвертая аксиома (принцип суперпозиции). При одновременном действии нескольких сил ускорение материальной точки равно векторной сумме ускорений, которые имела бы эта точка при действии каждой из сил в отдельности:
называют основным уравнением динамики точки
Третья аксиома (закон равенства действия и противодействия). Две материальных точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, (проходящей через эти точки), в противоположные стороны.
Четвертая аксиома (принцип суперпозиции). При одновременном действии нескольких сил ускорение материальной точки равно векторной сумме ускорений, которые имела бы эта точка при действии каждой из сил в отдельности:  , где:
, где:  27. Сила инерции.
Силы являются причиной любого изменения состояния движения, т.е. любого ускорения. Ускорение возникает в направлении действия силы. Кроме того, существуют так называемые силы инерции, которые возникают как следствие ускорений. Они направлены в сторону, противоположную ускорению. Силы инерции возникают только в системе отсчета, движущейся с ускорением, т. е. это кажущиеся силы.
27. Сила инерции.
Силы являются причиной любого изменения состояния движения, т.е. любого ускорения. Ускорение возникает в направлении действия силы. Кроме того, существуют так называемые силы инерции, которые возникают как следствие ускорений. Они направлены в сторону, противоположную ускорению. Силы инерции возникают только в системе отсчета, движущейся с ускорением, т. е. это кажущиеся силы.
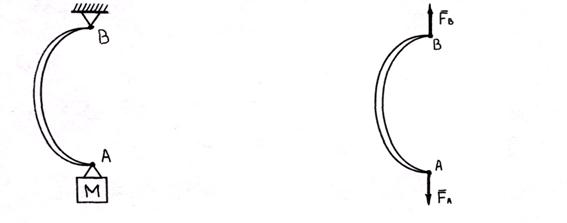
 2.Гибкая связь. Реакции нитей или цепей всегда направлены вдоль самих связей в сторону от тела к связи.
2.Гибкая связь. Реакции нитей или цепей всегда направлены вдоль самих связей в сторону от тела к связи.

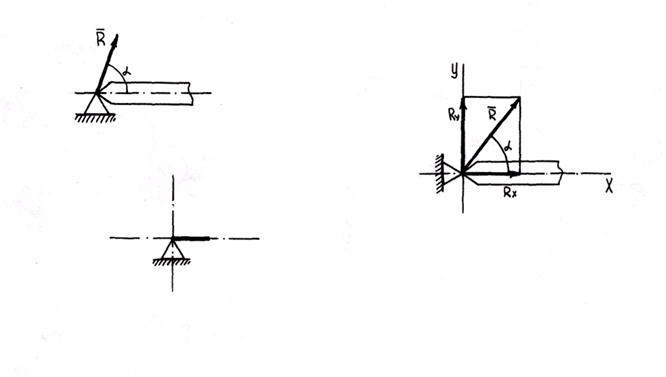 5. Шарнирно-неподвижная опора дает возможность телу свободно поворачиваться около шарнира, но препятствует поступательному перемещению тела в любом направлении, перпендикулярном оси шарнира.
5. Шарнирно-неподвижная опора дает возможность телу свободно поворачиваться около шарнира, но препятствует поступательному перемещению тела в любом направлении, перпендикулярном оси шарнира.


