
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция плоской световой волны на узкой щели. Зависимость светового действия щели от ее ширины и положения точки наблюдения на экране.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ИССЛЕДОВАНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ СВЕТА НА УЗКОЙ ЩЕЛИ. Цель работы: исследование явления дифракции света на узкой щели и определение ширины щели по ширине центрального дифракционного максимума.
Световая волна длиной l падает нормально к плоскости щели. За щелью установлена собирательная линза L, в фокальной плоскости которой находится экран Э. Параллельный пучок лучей, пройдя через щель, дифрагирует под разными углами вправо и влево от первоначального направления. Линза собирает параллельные пучки дифрагированных лучей в соответствующих точках экрана Э. Тип дифракции, при котором рассматривается дифракционная картина, образованная параллельными лучами, получил название дифракции в параллельных лучах, или дифракции Фраунгофера. Расчет дает формулу распределения интенсивности света на экране Эв зависимости от угла дифракции j в виде
где I0 – интенсивность света в середине дифракционной картины (в направлении j = 0); Ij - интенсивность света в точке, положение которой определяется данным значением угла j. При значении угла дифракции j, удовлетворяющему условию
Действительно, при Аналогично можно найти и интенсивности остальных максимумов. Расчеты показывают, что интенсивности центрального и следующих максимумов относятся как 1: 0,045: 0,016 и т. д.
Результирующую картину можно определить путем сложения этих двух картин с учетом интерференции волн, идущих от каждой из щелей. Очевидно, что в тех направлениях, в которых ни одна из щелей света не дает, не будет света и при двух параллельных щелях. Условие минимума интенсивности Если ширина щели а значительно меньше расстояния от щели до экрана, дифракция Фраунгофера будет иметь место и при отсутствии линзы между щелью и экраном (падающая на щель волна должна быть плоской). В этом случае лучи, идущие в точку Р от краев щели будут практически параллельны, так что все полученные ранее результаты остаются справедливыми. Измерив на опыте по дифракционной картине от узкой щели ширину центрального максимума и зная длину волны источника света, можно определить ширину щели. По картине дифракции от двух параллельных узких щелей, зная длину волны источника и ширину каждой щели, можно определить расстояние между ними. Рассмотрим применение метода зон Френеля для исследования распределения интенсивности света после прохождения узкой щели. Пусть параллельный пучок монохроматического света падает нормально на узкую щель шириной b (рис. 1) и длиной а >> b. В соответствии с принципом Гюйгенса-Френеля каждая точка щели является источником вторичных волн, колеблющихся в одной фазе, так как плоскость щели совпадает с фронтом волны. За щелью лучи света распространяются под разными углами. На рис. 1 изображены лучи, дифрагирующие на угол φ после прохождения щели. Обычно для исследования картины распределения интенсивности за щелью помещается собирающая линза и экран в фокальной плоскости этой линзы. Тогда лучи, выходящие из щели под одинаковым углом, будут собираться линзой в одной точке на экране, и в результате интерференции таких лучей будет наблюдаться темное или светлое пятно.
Рис. 1. Схема хода лучей при дифракции параллельного пучка света (дифракции Фраунгофера) на узкой щели: 1 – непрозрачный экран с щелью; 2 – линза; 3 – экран для наблюдения распределения интенсивности света Лучи, идущие от границ первой зоны Френеля из точек В и С, имеют разность хода При интерференции света от каждой пары соседних зон амплитуда результирующего колебания в точке Р равна нулю, т. к. эти зоны вызывают колебания с одинаковыми амплитудами, но по фазе отличаются на π. Если число зон, укладывающихся на щели, четное, то колебания каждой пары соседних зон гасят друг друга и результирующая амплитуда колебаний в точке Р будет равна нулю. Если на ширине щели укладывается нечетное число зон Френеля, то колебания от всех зон, кроме одной, будут полностью скомпенсированы. Амплитуда колебаний в точке Р будет определяться только одной зоной Френеля. Следует отметить, что ширина зоны Френеля зависит от угла дифракции φ. Из хода лучей на рис. 1 видно, что ширина одной зоны равна
или
В этом случае на экране в точке Р будет наблюдаться темное пятно. Целое число m называется порядком дифракционного минимума. Для нечетного числа зон, укладывающихся на щели,
В этом случае на экране в точке Р наблюдается светлое пятно. Отдельно следует рассмотреть лучи, идущие от щели под углом φ = 0. Такие лучи собираются линзой в центре экрана, и колебания, вызываемые в точке Р всеми участками щели, будут совершаться в одной фазе. Следовательно, в этом направлении будет наблюдаться самый интенсивный максимум. Этот центральный максимум называется максимум нулевого порядка. Ему соответствует около 90 % всего светового потока, выходящего из щели. Итак, используя метод зон Френеля, удалось довольно простым способом найти положение светлых и темных полос на экране при дифракции на узкой щели. Для более точного и детального выяснения картины распределения интенсивности света при дифракции на щели необходимо использовать принцип Гюйгенса-Френеля. Решение этой задачи можно провести следующим образом: щель разбивается на бесконечное число одинаковых, бесконечно узких полос, параллельных ребру щели. Вторичные волны, излучаемые такими полосками, будут цилиндрическими волнами с одинаковыми амплитудами. Суммирование этих волн сведется к интегрированию по всей ширине щели, и полученное выражение имеет вид
где А(j) – амплитуда колебаний в световой волне для точки на экране, в которой фокусируются лучи, идущие под углом j; А0 – амплитуда колебаний в световой волне в центре экрана:
Интенсивность света J(j) в различных точках экрана пропорциональна квадрату амплитуды А(j). Следовательно, используя уравнение (3), можем записать
где J0 – интенсивность света в центре экрана. График зависимости интенсивности света на экране J(j) показан на рис. 2. По горизонтальной оси отложена величина a, пропорциональная углу дифракции j. При практических наблюдениях дифракции угол j обычно мал, и с хорошей точностью можно использовать соотношение Тогда величина a с точностью до постоянного равна углу j.
Рис. 2. График распределения интенсивности света на экране: по вертикальной оси – интенсивность света; по горизонтальной – величина Используя формулы (2) и (5), можно найти относительные интенсивности максимумов
где m – порядок максимума. Численный расчет по формуле (6) показывает, что основная часть света приходится на центральный максимум. Ему соответствует около 90 % всего светового потока, выходящего из щели. Количество максимумов на экране и их ширина зависят от ширины щели и расстояния до экрана. При уменьшении ширины щели центральный максимум будет становиться шире, а количество боковых максимумов становится меньше. Если, например, ширина щели равна длине волны, b = λ, то sin φ = 1, следовательно, φ = π/2, т. е. ни одного дифракционного минимума наблюдаться не будет, экран будет весь освещен: больше к середине и меньше к краям. Это соответствует чистой дифракции без интерференции. Если же случай противоположный, т. е. ширина щели во много раз больше длины волны, то чередование боковых максимумов будет очень частым и при большей ширине щели картина чередования светлых и темных полос практически не различна. Для ширины центрального максимума в этом случае из соотношения (1) можно получить ту же величину, как в геометрической оптике. Присутствие линзы для наблюдения темных и светлых полос на экране необходимо при сравнительно небольшом расстоянии от щели до экрана. В случае когда ширина щели очень мала по сравнению с расстоянием до экрана, лучи от краев в точку Р будут практически параллельны и в отсутствии линзы между щелью и экраном.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1831; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 Рассмотрим дифракцию плоской монохроматической волны от щели. Щелью будем называть прямоугольное отверстие, ширина которого во много раз меньше его длины. Обозначим ширину щели а (рис. 1).
Рассмотрим дифракцию плоской монохроматической волны от щели. Щелью будем называть прямоугольное отверстие, ширина которого во много раз меньше его длины. Обозначим ширину щели а (рис. 1).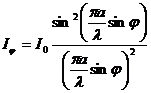 (1)
(1) (2)
(2) где k = ± 1, 2, 3,..., интенсивность света равна нулю. Последнее условие и количественные соотношения можно получить при решении задачи о дифракции на щели методом графического сложения амплитуд. Разобьем открытую часть волнистой поверхности на ряд узких параллельных полосок равной ширины. Каждую из этих полосок можно рассматривать как источник волн одинаковой амплитуды и фазы. Выражая амплитуды каждой полоски векторами равной длины, найдем результирующую амплитуду, пользуясь графическим методом сложения векторов. Результаты при разных углах дифракции представлены на рис. 2. При j = 0 (рис. 2а), т. е. в фокусе линзы L, амплитуда колебаний А0 будет максимальной. В направлении, при котором крайние полоски отличаются по фазе на p
где k = ± 1, 2, 3,..., интенсивность света равна нулю. Последнее условие и количественные соотношения можно получить при решении задачи о дифракции на щели методом графического сложения амплитуд. Разобьем открытую часть волнистой поверхности на ряд узких параллельных полосок равной ширины. Каждую из этих полосок можно рассматривать как источник волн одинаковой амплитуды и фазы. Выражая амплитуды каждой полоски векторами равной длины, найдем результирующую амплитуду, пользуясь графическим методом сложения векторов. Результаты при разных углах дифракции представлены на рис. 2. При j = 0 (рис. 2а), т. е. в фокусе линзы L, амплитуда колебаний А0 будет максимальной. В направлении, при котором крайние полоски отличаются по фазе на p  , результирующая амплитуда равна
, результирующая амплитуда равна  (рис 2б), так как последняя равна диаметру полуокружности, длина которой А0. В направлении, при котором крайние полоски отличаются по фазе на 2p
(рис 2б), так как последняя равна диаметру полуокружности, длина которой А0. В направлении, при котором крайние полоски отличаются по фазе на 2p  , результирующая амплитуда обращается в нуль (рис. 2в). Амплитуда равна нулю во всех случаях, когда разность хода между крайними лучами D равна l, 2l, 3l,...,kl, т. е. минимумы освещенности соответствуют направлениям
, результирующая амплитуда обращается в нуль (рис. 2в). Амплитуда равна нулю во всех случаях, когда разность хода между крайними лучами D равна l, 2l, 3l,...,kl, т. е. минимумы освещенности соответствуют направлениям  , где k – целое число, т. к. D = asinj.
, где k – целое число, т. к. D = asinj.
 . Интенсивность света I0 определяется квадратом А0. Следующие максимумы значительно уступают по величине центральному.
. Интенсивность света I0 определяется квадратом А0. Следующие максимумы значительно уступают по величине центральному. амплитуда колебаний
амплитуда колебаний  (рис. 2г), интенсивность первого максимума
(рис. 2г), интенсивность первого максимума  /
/ Рассмотрим дифракцию от двух параллельных щелей одинаковой ширины а и расположенных на расстоянии b друг от друга. Дифракционная картина наблюдается в фокальной плоскости линзы L(рис. 4а). На экран со щелями падает плоская монохроматическая волна длиной l. Положение дифракционных максимумов и минимумов от одной щели не зависит от ее положения, а определяется направлением дифрагированных лучей. Это значит, что перемещение щели параллельно самой себе не приводит к изменению дифракционной картины. Следовательно, картины, создаваемые каждой щелью в отдельности будут совершенно одинаковыми.
Рассмотрим дифракцию от двух параллельных щелей одинаковой ширины а и расположенных на расстоянии b друг от друга. Дифракционная картина наблюдается в фокальной плоскости линзы L(рис. 4а). На экран со щелями падает плоская монохроматическая волна длиной l. Положение дифракционных максимумов и минимумов от одной щели не зависит от ее положения, а определяется направлением дифрагированных лучей. Это значит, что перемещение щели параллельно самой себе не приводит к изменению дифракционной картины. Следовательно, картины, создаваемые каждой щелью в отдельности будут совершенно одинаковыми. , где k = ±1, 2, 3, …, выполняется и в данном случае. Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, взаимно уничтожаются. Возникают добавочные минимумы. Они будут наблюдаться в тех направлениях, которым соответствует разность хода
, где k = ±1, 2, 3, …, выполняется и в данном случае. Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, взаимно уничтожаются. Возникают добавочные минимумы. Они будут наблюдаться в тех направлениях, которым соответствует разность хода  для волн, идущих от соответственных точек (отстоящих на расстоянии а + b) обеих щелей. Такие направления определяются (см. рис. 4а) условием
для волн, идущих от соответственных точек (отстоящих на расстоянии а + b) обеих щелей. Такие направления определяются (см. рис. 4а) условием  , где m = ±0, 1, 2, 3, …. В направлениях, определяемых из условия
, где m = ±0, 1, 2, 3, …. В направлениях, определяемых из условия  , где m = ±0, 1, 2, 3, … действие одной щели усиливает действие другой. Этим направлениям соответствуют максимумы интенсивности. Расстояние между первичными минимумами (от одной щели) зависит от ширины щели. Если
, где m = ±0, 1, 2, 3, … действие одной щели усиливает действие другой. Этим направлениям соответствуют максимумы интенсивности. Расстояние между первичными минимумами (от одной щели) зависит от ширины щели. Если  , то между двумя первичными минимумами может расположиться несколько минимумов и максимумов. Кривая на рис. 4б показывает распределение интенсивностей света при дифракции на двух параллельных щелях.
, то между двумя первичными минимумами может расположиться несколько минимумов и максимумов. Кривая на рис. 4б показывает распределение интенсивностей света при дифракции на двух параллельных щелях. Разобьем щель на зоны Френеля, имеющие вид полосок, параллельных ребру щели. По определению зоны Френеля лучи, идущие от краев каждой зоны, должны иметь разность хода, равную половине длины волны
Разобьем щель на зоны Френеля, имеющие вид полосок, параллельных ребру щели. По определению зоны Френеля лучи, идущие от краев каждой зоны, должны иметь разность хода, равную половине длины волны  .
. .
. . (Число зон равно отношению
. (Число зон равно отношению  , где b – ширина щели). Для четного числа зон выполняется условие
, где b – ширина щели). Для четного числа зон выполняется условие , где m = 1, 2, 3 …;
, где m = 1, 2, 3 …; . (1)
. (1) , где m = 0, 1, 2, 3…, или
, где m = 0, 1, 2, 3…, или . (2)
. (2) , (3)
, (3) . (4)
. (4) , (5)
, (5) .
.
 , (6)
, (6)


