
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика вращательного движения вокруг неподвижной оси . Момент импульса. Закон сохранения момента импульса.Содержание книги
Поиск на нашем сайте
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ Основные формулы • Момент силы F,действующей на тело, относительно оси вращения
• Момент инерции относительно оси вращения:а) материальной точки.J=mr2,где т —масса точки;r —расстояние ее от оси вращения; б) дискретного твердого тела
в) сплошного твердого тела
dm=dV и Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях). Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр. Момент импульса замкнутой системы сохраняется. Момент импульса является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой неподвижной точки (или сумма моментов относительно любой неподвижной оси) для замкнутой системы остается постоянной со временем. Производная момента импульса по времени есть момент силы:
Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного) момента внешних сил:
где 11. Постулаты частной теории относительности. Преобразование Лоренца. Относительность одновременности пространственно разделенных независимых событий. Исторически именно закон сложения скоростей (5) показал ограниченность галилеевых представлений о свойствах пространства и времени.Действительно, согласно этому закону по отношению к системе отсчета, догоняющей свет, скорость света должна быть меньше, чем по отношению к покоящейся системе, т. е. должна быть равна (c - V). При противоположном движении скорость света должна быть равна (с + V). На самом деле это не наблюдается. Из опытов следует, что с - скорость света в вакууме в различных инерциальных системах отсчета имеет одно и то же значение.Впервые постоянство скорости света было обнаружено в опытах Майкельсона и Морли, поставленных в период с 1880 по 1887 г. В этих опытах в качестве движущейся системы отсчета использовалась Земля, которая движется по орбите вокруг Солнца со скоростью Преобразования Лоренца псевдоевклидова пространства сигнатуры Определение Преобразование Лоренца (лоренцево преобразование) псевдоевклидова векторного пространства
где треугольными скобками обозначено индефинитное скалярное произведение Аналогично, преобразование Лоренца (лоренцево преобразование) псевдоевклидова аффинного пространства — это аффинное преобразование, сохраняющее расстояние между точками этого пространства (это расстояние определяется как длина вектора, соединяющего данные точки, с помощью индефинитного скалярного произведения).Относительность одновременности событий В механике Ньютона одновременность двух событий абсолютна и не зависит от системы отсчёта. Это значит, что если два события происходят в системе K в моменты времени t и t1, а в системе K’соответственно в моменты времени t’и t’1, то поскольку t=t’, промежуток времени между двумя событиями одинаков в обеих системах отсчёта В отличие от классической механики, в специальной теории относительности одновременность двух событий, происходящих в разных точках пространства, относительна: события, одновременные в одной инерциальной системе отсчёта, не одновременны в других инерциальных системах2, движущихся относительно первой. На рисунке (см. ниже) расположена схема эксперимента, который это иллюстрирует. Система отсчета K связана с Землёй, система K’—с вагоном, движущимся относительно Земли прямолинейно и равномерно со скоростью v. На Земле и в вагоне отмечены точки А, М, В и соответственно А’, M’и В’, причем АМ=МВ и А’M’=M’B’. В момент, когда указанные точки совпадают, в точках А и В происходят события —ударяют две молнии. В системе К сигналы от обоих вспышек придут в точку М одновременно, так как АМ=МВ, и скорость света одинакова во всех направлениях. В системе К’, связанной с вагоном, сигнал из точки В’придет в точку M’раньше, чем из точки А’, ибо скорость света одинакова во всех направлениях, но М’ движется навстречу сигналу пущенному из точки B’ и удаляется от сигнала, пущенного из точки А’. Значит, события в точкахА’иB’не одновременны: события в точке B’произошло раньше, чем в точке A’. Если бы вагон двигался в обратном направлении, то получился бы обратный результат. Понятие одновременности пространственно разделенных событий относительно. Из постулатов теории относительности и существования конечной скорости распространения сигналов следует, что в разных инерциальных системах отсчёта время протекает по-разному.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.69.138 (0.008 с.) |

 ,где
,где 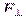 — проекция силы F на плоскость, перпендикулярную оси вращения; l — плечо силы F (кратчайшее расстояние от оси вращения до линии действия силы).
— проекция силы F на плоскость, перпендикулярную оси вращения; l — плечо силы F (кратчайшее расстояние от оси вращения до линии действия силы). где
где  — масса i-го элемента тела; ri — расстояние этого элемента от оси вращения; п — число элементов тела;
— масса i-го элемента тела; ri — расстояние этого элемента от оси вращения; п — число элементов тела;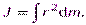 Если тело однородно, т. е. его плотность
Если тело однородно, т. е. его плотность  одинакова по всему объему, то
одинакова по всему объему, то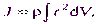 где V —объем тела.Моме́нти́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1].
где V —объем тела.Моме́нти́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1].

 — момент одной из сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется).
— момент одной из сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется). . Скорость света вдоль направления движения Земли сравнивалась со скоростью света поперек этого направления. Скорости оказались одинаковыми.Из уравнений Максвелла, описывающих электромагнитные явления, также вытекает постоянство скорости света.В 1905 г. Эйнштейн предложил отказаться от поиска объяснений, почему скорость светавсех инерциальных системах отсчета оказывается одинаковой. Им была высказана смелая мысль о том, что постоянство скорости света является фундаментальным свойством природы, которое нужно констатировать как факт.Постоянство скорости света в вакууме во всех инерциальных системах отсчета известно под названием постулата Эйнштейна. Постулат это то жесамое, что и аксиома: "бесспорная, не требующая доказательств истина".Другим постулатом является принцип относительности Эйнштейна:законы природы одинаковы во всех инерциальных системах отсчета или уравнения, выражающие законы природы, инвариантны к преобразованиям Лоренца.Из этого постулата следует, что никакими опытами (механическими, электрическими, оптическими и др.), проведенными внутри данной системы отсчета, нельзя установить находится ли она в покое, или движется равномерно и прямолинейно.Преобразова́ния Ло́ренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющиедлины или, что эквивалентно, скалярное произведение векторов.
. Скорость света вдоль направления движения Земли сравнивалась со скоростью света поперек этого направления. Скорости оказались одинаковыми.Из уравнений Максвелла, описывающих электромагнитные явления, также вытекает постоянство скорости света.В 1905 г. Эйнштейн предложил отказаться от поиска объяснений, почему скорость светавсех инерциальных системах отсчета оказывается одинаковой. Им была высказана смелая мысль о том, что постоянство скорости света является фундаментальным свойством природы, которое нужно констатировать как факт.Постоянство скорости света в вакууме во всех инерциальных системах отсчета известно под названием постулата Эйнштейна. Постулат это то жесамое, что и аксиома: "бесспорная, не требующая доказательств истина".Другим постулатом является принцип относительности Эйнштейна:законы природы одинаковы во всех инерциальных системах отсчета или уравнения, выражающие законы природы, инвариантны к преобразованиям Лоренца.Из этого постулата следует, что никакими опытами (механическими, электрическими, оптическими и др.), проведенными внутри данной системы отсчета, нельзя установить находится ли она в покое, или движется равномерно и прямолинейно.Преобразова́ния Ло́ренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющиедлины или, что эквивалентно, скалярное произведение векторов. находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространства выступает четырёхмерный пространственно-временной континуум (пространство Минковского).
находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространства выступает четырёхмерный пространственно-временной континуум (пространство Минковского). — это линейное преобразование
— это линейное преобразование  , сохраняющее индефинитное скалярное произведение векторов. Это означает, что для любых двух векторов
, сохраняющее индефинитное скалярное произведение векторов. Это означает, что для любых двух векторов  выполняется равенство
выполняется равенство
 в псевдоевклидовом пространстве
в псевдоевклидовом пространстве 


