Особенность работы сил электростатического поля. Циркуляция вектора напряженности. Определение потенциала и разности потенциалов. Принцип суперпозиции для потенциалов.
Похожие статьи вашей тематики
Как известно их механики материальной точки, эта сила будет совершать механическую работу, не зависимо от того, какова природа силы.
 Элементарная работа силы Элементарная работа силы  на перемещении на перемещении 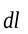 равна: равна:

В силу того, что кулоновская сила центральная, т.е. зависит только от расстояния r,

Работа силы при перемещении заряда q из точки 1 в точку 2 равна:

Из формулы (1) видно, что эта работа не зависит от того пути, по которому перемещался заряд q, а зависит только от начального и конечного положений этого заряда.
Очевидно, что если мы каким-то «насильственным» образом переместим заряд q из точки 1 в точку 2, то мы совершаем работу против сил поля, которая также дается формулой (1).
Если вместо заряда  мы имеем систему зарядов мы имеем систему зарядов  , то общая работа по перемещению заряда q на основании принципа суперпозиции полей, может быть представлена в виде суммы работ: , то общая работа по перемещению заряда q на основании принципа суперпозиции полей, может быть представлена в виде суммы работ:

Циркуляция вектора напряженности  электростатического поля равна нулю, а само электростатическое поле является потенциальным. электростатического поля равна нулю, а само электростатическое поле является потенциальным.
 Пусть на замкнутый контур L опирается некоторая поверхность S. Пусть на замкнутый контур L опирается некоторая поверхность S.
Согласно теореме Стакса:
 , где , где
 : а символический вектор-оператор «набла»: : а символический вектор-оператор «набла»: 
Согласно  , откуда , откуда 
Потенциал электрического поля-это скалярная величина равная отношению потенциальной энергии к величине заряда.
Развонсть потенциалов-называют также напряжением, равна работе сид электростатического поля при перемещении единичного положительного заряда из начальной точки в конечную.
Принцип суперпозиции потенциала:
Потенциал поля, созданного группой зарядов в произвольной точке = сумме потенциалов полей, созданных каждым зарядом.
Поток вектора напряженности и его геометрический смысл. Теорема Остроградского-Гаусса (ОГ) для электростатического поля. Пример использования ОГ.
Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля(Φ). Понятие потока вектора  аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора  пропорционален числу линий напряженности, пронизывающих элементарную площадку ΔS (рис. 1.6). пропорционален числу линий напряженности, пронизывающих элементарную площадку ΔS (рис. 1.6).
Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора  на площадь ΔS и на косинус угла α между вектором на площадь ΔS и на косинус угла α между вектором  и нормалью и нормалью  к площадке называется элементарным потоком вектора напряженности через площадку ΔS: к площадке называется элементарным потоком вектора напряженности через площадку ΔS:
 , ,
где  – проекция вектора – проекция вектора  на нормаль на нормаль  к площадке к площадке  ; ;  ‑ единичный вектор, перпендикулярный площадке ‑ единичный вектор, перпендикулярный площадке  . .
 К определению элементарного потока ΔΦ. К определению элементарного потока ΔΦ.
Полный поток вектора напряженности  сквозь поверхность сквозь поверхность  в общем случае равен: в общем случае равен:

где  . (Выбор нормали . (Выбор нормали  условен, но в случае замкнутых поверхностей условен, но в случае замкнутых поверхностей  принято брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль). Единица измерения потока ‑ В·м. принято брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль). Единица измерения потока ‑ В·м.

Применение теоремы Остроградского–Гаусса особенно удобно для расчета электростатических полей симметричных систем зарядов. В этом случае можно так выбрать гауссову поверхность, что поток напряженности поля через нее легко выражается через искомое значение модуля вектора. Решение задачи о нахождении напряженности поля в какой-либо точке пространства должно осуществляться следующим образом:
1. Исходя из симметрии распределения заданной системы зарядов в пространстве необходимо построить силовые линии поля, т.е. определить направление вектора в любой точке пространства.
2. Выбрать “удобную” замкнутую гауссову поверхность, отвечающую следующим требованиям:
а) она должна проходить через исследуемую точку;
б) площадь поверхности должна быть известна;
в) модуль напряженности поля должен быть постоянен в точках всей поверхности или хотя бы ее части;
г) угол между и внешней нормалью к поверхности должен быть известен в любой точке поверхности (это обеспечивается выполнением п. 1).
3. Определить поток напряженности поля через выбранную поверхность.

|