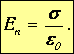Эквипотенциальные поверхности. Связь между потенциалом и напряженностью электрического поля.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью.

Между двумя любыми точками на эквипотзенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю. Это означает, что вектор силы в любой точке траектории движения заряда по эквипотенциальной поверхности перпендикулярен вектору скорости. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности.

Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд (рис. 112).

Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности (рис. 113).

Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой – потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: d A = q E d l, эта же работа равна убыли потенциальной энергии заряда q: d A = - d W _п = - q d ,где d - изменение потенциала электрического поля на длине перемещения d l. Приравнивая правые части выражений, получаем: E d l = -d или в декартовой системе координат

E_x d x + E_y d y + E_z d z = -d , (1.8)

где E_x, E_y, E_z - проекции вектора напряженности на оси системы координат.

Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

откуда

.Стоящее в скобках выражение является градиентом потенциала j, т. е.

E = - grad = -Ñ .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

 

7. Проводники в электрическом поле (электрическое поле, потенциал и заряды внутри проводника). Распределение зарядов на заряженном проводнике. Его электрическое поле.

1. Свободные заряды в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому для равновесия зарядов в проводнике должны выполняться следующие условия:

2. Напряженность поля внутри проводника должна быть равна нулю , т.к. т.е. потенциал внутри проводника должен быть постоянным.

3. Напряженность поля на поверхности проводника должна быть перпендикулярна поверхности

Следовательно, поверхность проводника при равновесии зарядов является эквипотенциальной.

При равновесии зарядов ни в каком месте внутри проводника не может быть избыточных зарядов – все они распределены по поверхности проводника с некоторой плотностью σ.

Рассмотрим замкнутую поверхность в форме цилиндра, образующие которого перпендикулярны поверхности проводника. На поверхности проводника расположены свободные заряды с поверхностной плотностью σ.

Т.к. внутри проводника зарядов нет, то поток через поверхность цилиндра внутри проводника равен нулю. Поток через верхнюю часть цилиндра вне проводника по теореме Гаусса равен

т.е. вектор электрического смещения равен поверхностной плотности свободных зарядов проводника или

2. При внесении незаряженного проводника во внешнее электростатическое поле свободные заряды начнут перемещаться: положительные - по полю, отрицательные – против поля. Тогда с одной стороны проводника будут накапливаться положительные, а с другой отрицательные заряды. Эти заряды называются ИНДУЦИРОВАННЫМИ.

 

Электрические заряды, располагающиеся на поверхности проводника с некоторой плотностью s создают вне проводника электрическое поле. Вблизи поверхности проводника напряженность поля направлена по нормали n в каждой точке поверхности, то есть

так как силовые линии перпендикулярны эквипотенциальным поверхностям. Для вычисления поля вблизи проводника снова используем теорему Остроградского-Гаусса. В качестве воображаемой поверхности возьмем поверхность бесконечно малого цилиндра, расположенного перпендикулярно проводнику так, что одно из его оснований находится вне проводника, а другое - внутри (рис. 2.2).

Рис. 2.2. Электрическое поле вблизи поверхности изолированного заряженного проводника

В этом случае поток через основание внутри проводника равен нулю, так как внутри проводника нет поля. Далее, поток через боковые стенки также равен нулю, поскольку они параллельны вектору напряженности поля. Остается поток через основание площадью dS вне проводника. Тогда полный поток вектора электрической напряженности E через поверхность цилиндра будет равен

(2.1)

Согласно теореме Остроградского-Гаусса,

_откуда