
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Токи при замыкании цепи и размыкании цепи.Содержание книги
Поиск на нашем сайте
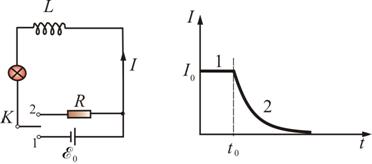
По правилу Ленца дополнительные токи, возникающие в проводниках вследствие самоиндукции, всегда направлены так, чтобы воспрепятствовать изменениям тока, текущего в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а постепенно. Сначала найдем характер изменения тока при размыкании цепи (рис. 3).
IR= Перепишем это выражение следующим образом:
Это линейное однородное дифференциальное уравнение 1-го порядка. Его легко проинтегрировать, разделив переменные:
Потенцирование этого соотношения дает:
Это выражение является общим решением дифференциального уравнения первого порядка. При t=0, сила тока равна:
Отсюда видно, что сила тока убывает по экспоненте (рис. 4).
После преобразования приходим к линейному неоднородному уравнению:
Общее решение этого уравнения можно получить, прибавив любое его частное решение к общему решению однородного уравнения.
В момент времени t=0, I=0. Отсюда, для сonst получается значение сonst = - I0. То есть Если цепь содержит катушку с железным сердечником, ЭДС самоиндукции будет определяться
В этом случае за счет слагаемого
Энергия магнитного поля. Энергия магнитного поля контура с током. Энергия магнитного поля соленоида, плотность энергии магнитного поля. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА Вокруг проводника с током существует магнитное поле, которое обладает энергией. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Энергия магнитного поля контура с током:
Рассмотрим случай, о котором мы уже говорили (рис. 5.6).
Рис. 5.6 Сначала замкнем соленоид L на источник ЭДС
Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией
Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида:
Подставим эти значения в формулу (5.5.3):
Обозначим w – плотность энергии, или энергия в объеме V, тогда
но т.к.
Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле
а плотность энергии
Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника:
Т.к. в вакууме
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.110 (0.007 с.) |

 Рис. 3
Рис. 3
 . Под действием этой ЭДС в цепи будет течь постоянный ток:
. Под действием этой ЭДС в цепи будет течь постоянный ток:  .
В момент времени t=0 отключим ЭДС, переведем переключатель П в положение 2.Как только сила тока в цепи станет убывать возникает ЭДС самоиндукции. Закон Ома:
.
В момент времени t=0 отключим ЭДС, переведем переключатель П в положение 2.Как только сила тока в цепи станет убывать возникает ЭДС самоиндукции. Закон Ома:
 =L
=L  .
.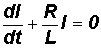 .
. , откуда
, откуда  .
. .
. , следовательно, const = I0, тогда
, следовательно, const = I0, тогда  .
.
 .
. .
. ,(см. рис. 4).
,(см. рис. 4). .
. ЭДСсамоиндукции может достигать очень больших значений, и сила тока может значительно превзойти I0.
ЭДСсамоиндукции может достигать очень больших значений, и сила тока может значительно превзойти I0.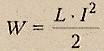


 , в нем будет протекать ток
, в нем будет протекать ток  . Затем в момент времени
. Затем в момент времени  переключим ключ в положение 2 – замкнем соленоид на сопротивление R. В цепи будет течь убывающий ток I. При этом будет совершена работа:
переключим ключ в положение 2 – замкнем соленоид на сопротивление R. В цепи будет течь убывающий ток I. При этом будет совершена работа:  , или
, или
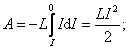
 ,
,
 ,
,
 .
. ; отсюда
; отсюда 

 ,
,
 , то
, то или
или 
 ,
,

 , отсюда
, отсюда  .
. , имеем
, имеем



