
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимодействие двух проводников с токомСодержание книги
Поиск на нашем сайте
Применим закон Ампера для вычисления силы взаимодействия двух длинных прямолинейных проводников с токами I 1 и I 2, находящихся на расстоянии d друг от друга (рис. 6.26).
Рис. 6.26. Силовое взаимодействие прямолинейных токов: Проводник с током I 1 создает кольцевое магнитное поле, величина которого в месте нахождения второго проводника равна
Это поле направлено «от нас» ортогонально плоскости рисунка. Элемент второго проводника
Подставляя (6.23) в (6.24), получим
При параллельных токах сила F 21 направлена к первому проводнику (притяжение), при антипараллельных — в обратную сторону (отталкивание). Аналогично на элемент Итак, сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников, рассчитанная на элемент длины
Эффект Холла. Эффект, открытый американским физиком Эдвином Гербертом Холлом в 1879 году, заключается в явлении возникновения поперечной разности потенциалов в полупроводнике, по которому протекает электрический ток и существует магнитное поле Н, перпендикулярное направлению тока. Физическая природа эффекта Холла заключается в том, что на движущийся носитель тока в магнитном поле с индукцией В действует сила Лоренца где v –скорость носителя; q – его заряд. Направление силы Лоренца определяется правилом левой руки. Если проводник n -типа проводимости, то электроны будут смещаться влево к внешней стороне пластины, заряжая её отрицательно (рис. 6.8). В полупроводника p -типа проводимости при том же направлении тока сила Лоренца будет смещать дырки в том же направлении. При этом левая внешняя сторона пластинки зарядится положительно.
Если угол между вектором скорости носителей v и вектором магнитной индукции B равен 90о, то величина силы Лоренца рассчитывается по формуле F л= qvB, (6.12) где v – средняя дрейфовая скорость носителей заряда, м/c. Электрическое поле между поперечными гранями пластинки равно где U х» (0,6…1)·10-4 В - разность потенциалов между поперечными гранями пластинки, называемая эдс Холла; а – ширина пластинки. Поле Е х действует на электроны с силой F =- qE х, направленной против силы Лоренца F л. При выполнении условия F л= F поперечное электрическое поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов на боковых гранях пластины прекращается. Тогда из равенства qvB = qE х следует E х= vB. Дрейфовая скорость носителей тока определяется из выражения где j – плотность тока, А/м2, n – концентрация электронов, м-3, Тогда выражение для поля Е х приобретает вид Умножив обе части равенства (6.15) на ширину пластинки а, получаем формулу для эдс Холла Формула (6.16) обычно записывается в виде где С учетом разброса средней скорости дрейфа электронов в полупроводнике значение коэффициента Холла определяется из выражения где А =1,18 для полупроводников с преимущественным рассеянием носителей заряда на тепловых колебаниях кристаллической решетки; А =1,93 при рассеянии на ионизированных примесях. Для дырочных полупроводников коэффициент Холла рассчитывается по формуле где q и p –заряд и концентрация дырок, соответственно. При смешенной электронно-дырочной проводимости величина коэффициента Холла рассчитывается по формуле где μ n и μ p – подвижности электронов и дырок, соответственно. Из формулы (6.20) следует, что в собственных полупроводниках при выполнении условия ni = pi значение коэффициента Холла равно
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 757; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.255 (0.01 с.) |



 испытывает со стороны этого поля действие силы Ампера
испытывает со стороны этого поля действие силы Ампера


 , Н, (6.11)
, Н, (6.11) , В/м, (6.13)
, В/м, (6.13) , (6.14)
, (6.14) . (6.15)
. (6.15) ,В. (6.16)
,В. (6.16) , (6.17)
, (6.17) – коэффициент Холла, м3/Кл.
– коэффициент Холла, м3/Кл.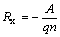 , (6.18)
, (6.18) , (6.19)
, (6.19) , (6.20)
, (6.20)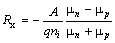 . (6.21)
. (6.21)


