
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитная индукция. Токи Фуко. Скин-эффект.Содержание книги
Поиск на нашем сайте
Если индукционные токи возбуждаются в массивных сплошных проводниках, то они могут достигать больших значений и вызывать сильный нагрев проводника. Впервые явление нагрева массивных проводников в переменном магнитном поле наблюдал французский физик Ж. Фуко (1819–1868) в 1855 г. Индукционные токи, возникающие в массивных сплошных проводниках, находящихся в переменном магнитном поле называют вихревыми токами или токами Фуко. Линии такого тока, как и силовые линии вихревого электрического поля, этот ток индуцирующего, замкнуты. Согласно правилу Ленца токи Фуко направлены так, чтобы своим действием противодействовать причине, которая их вызвала. Поэтому проводники, движущиеся в сильном магнитном поле, тормозятся в результате взаимодействия вихревых токов и магнитного поля. Это используется в демпферных приспособлениях для успокоения гальванометров, сейсмографов и рамок иных измерительных приборов. Вихревые токи вызывают сильный нагрев проводника, что позволяет использовать их для плавления металлов в вакууме, получая особо чистые материалы. Индукционные печи, которые используются при этом, представляют собой катушки, по которым проходит большой высокочастотный ток. При помещении внутрь катушки проводящего тела в нем возникают вихревые токи, вызывающие его сильный нагрев. Таким способом осуществляется прогрев металлических частей вакуумных установок. В некоторых случаях токи Фуко вредны. Они вызывают сильный нагрев сердечников трансформаторов и поэтому их изготавливают из тонких пластин, разделенных слоем диэлектрика. Токами Фуко обусловлен и так называемый скин-эффект (поверхностный эффект). Если в проводах текут переменные токи, то токи Фуко ослабляют ток внутри провода и усиливают его около поверхности. Ток как бы вытесняется на поверхность проводника. Поэтому в высокочастотных проводах «бесполезную» внутреннюю часть удаляют. Скин-эффект используется для поверхностной закалки стали. Явление самоиндукции. Коэффициент самоиндукции. Коэффициент самоиндукции соленоида. ЭДС самоиндукции.
В любом случае, когда по контуру протекает электрический ток, создается магнитное поле. При этом всегда имеется магнитный поток Ф, проходящий через поверхность, ограниченную рассматриваемым контуром. Любое изменение силы тока в контуре приводит к изменению магнитного поля, сцепленного с контуром, а это в свою очередь вызывает появление индукционного тока. Это явление получило название явления самоиндукции: возникновение ЭДС индукции в проводнике при изменении в нем тока. Из закона Био-Савара-Лапласа следует
т.е. магнитный поток, сцепленный с контуром, пропорционален току I в контуре Ф= LI. [ L ] = Гн (Генри). 1 Гн - индуктивность такого контура, магнитный поток самоиндукции которого при токе 1 А равен 1 Вб. Рассчитаем индуктивность L соленоида:
магнитная индукция В соленоида
т.е. индуктивность зависит от геометрических размеров соленоида ( Применяя к явлению самоиндукции закон Фарадея, получим, что ЭДС самоиндукции
Если L = const
где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем возрастает, то ЭДС САМОИНДУКЦИИ
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.42.61 (0.007 с.) |

 Самоиндукция
Самоиндукция





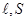 ), числа витков и магнитной проницаемости сердечника соленоида. Поэтому можно сказать, что индуктивность L аналог емкости С уединенного проводника, которая также зависит от геометрических размеров, от формы и диэлектрической проницаемости среды.
), числа витков и магнитной проницаемости сердечника соленоида. Поэтому можно сказать, что индуктивность L аналог емкости С уединенного проводника, которая также зависит от геометрических размеров, от формы и диэлектрической проницаемости среды.

 , и
, и  т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником и тормозит его возрастание. Если ток со временем убывает, то
т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником и тормозит его возрастание. Если ток со временем убывает, то  и
и  т.е.индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Следовательно, контур, обладающий индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока тормозится, тем сильнее, чем больше индуктивность контура.
т.е.индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Следовательно, контур, обладающий индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока тормозится, тем сильнее, чем больше индуктивность контура.



