

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Расчёт с помощью закона бс магнитного поля на оси кругового витка с током. Аналогия с электрическим полем диаполя.
Напряженностью магнитного поля называется отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля.Напряженность изображается вектором H, имеющим направление вектора механической силы f:  .Элемент тока — векторная величина, равная произведению тока проводимости вдоль линейного проводника и бесконечно малого отрезка этого проводника. .Элемент тока — векторная величина, равная произведению тока проводимости вдоль линейного проводника и бесконечно малого отрезка этого проводника.  .Примечание. Элемент тока имеет направление, совпадающее с направлением этого отрезка.Закон Био—Савара—Лапласа — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. .Примечание. Элемент тока имеет направление, совпадающее с направлением этого отрезка.Закон Био—Савара—Лапласа — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.

Круговой проводник с током. 
Возьмем проводник, согнутый по кругу в виде витка, и пропустим по нему ток (рис. 75). Из чертежа видно, что магнитные линии замыкаются вокруг проводника с током и имеют форму окружностей. Магнитные линии с одной стороны входят в плоскость кругового проводника, с другой — выходят.Направление поля кругового тока можно определить, пользуясь «правилом буравчика».Буравчик нужно расположить по оси кругового тока перпендикулярно его плоскости. Если теперь вращать ручку буравчика по направлению тока в контуре, то поступательное движение буравчика покажет направление магнитного поля. Напряженность магнитного поля в центре витка с током определяется по формуле: 
35.Поток вектора магнитной индукции(магнитный поток) и его геометрический смысл.Теорема ОГ для магнитного поля.
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная  где Bn=В cos a — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos a (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено: оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции ФB через произвольную поверхность S где Bn=В cos a — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos a (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено: оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции ФB через произвольную поверхность S  Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, Bn=B=const и Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, Bn=B=const и 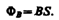 Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл×м2). Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл×м2). Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: 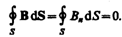 Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные. В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью m, согласно, равна Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные. В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью m, согласно, равна 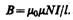 Магнитный поток сквозь один виток соленоида площадью S равен а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением, Магнитный поток сквозь один виток соленоида площадью S равен а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,  . Магнитный момент контура с током. Контур с током в магнитном поле. Опыт показывает, что электрические токи взаимодействуют между собой, напрмер, токи I притягиваются, а токи отталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром. Ориентацию его в пространстве характеризует направление нормали n(вектор) к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали n(вектор) (см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении. . Магнитный момент контура с током. Контур с током в магнитном поле. Опыт показывает, что электрические токи взаимодействуют между собой, напрмер, токи I притягиваются, а токи отталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром. Ориентацию его в пространстве характеризует направление нормали n(вектор) к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали n(вектор) (см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении.  Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна IS, т.е. Mmax ~ IS, где I -ток контуре, S - площадь контура с током, (рис. 1). Векторную величину Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна IS, т.е. Mmax ~ IS, где I -ток контуре, S - площадь контура с током, (рис. 1). Векторную величину  (1) называют магнитным моментом контура, который в СИ измеряется в А×м2. На пробные контуры с разными рm, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты М, но отношение Мmax/pm будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией В = Мmax/pm Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно установившегося во внешнем магнитном поле(см.рис.2) Поле вектора В можно представить с помощью силовых линий, (см. рис. 2), как и поле вектора таким образом В является аналогом Е.Магнитная индукция в СИ измеряется в теслах: 1 Тл=1 Нм/1 А×м2. Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 А м2, действует максимальный вращающий момент, равный 1 Нм. На контур с током, помещенный в магнитное поле с индукцией действует вращающий момент (1) называют магнитным моментом контура, который в СИ измеряется в А×м2. На пробные контуры с разными рm, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты М, но отношение Мmax/pm будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией В = Мmax/pm Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно установившегося во внешнем магнитном поле(см.рис.2) Поле вектора В можно представить с помощью силовых линий, (см. рис. 2), как и поле вектора таким образом В является аналогом Е.Магнитная индукция в СИ измеряется в теслах: 1 Тл=1 Нм/1 А×м2. Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 А м2, действует максимальный вращающий момент, равный 1 Нм. На контур с током, помещенный в магнитное поле с индукцией действует вращающий момент  Величина его M =. Величина его M =.  Работа по перемещению проводника и контура с током в магнитном поле. Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле В,перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор В сонаправлен с n. Работа по перемещению проводника и контура с током в магнитном поле. Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле В,перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор В сонаправлен с n. 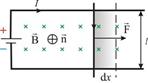 На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: Пусть проводник l переместится параллельно самому себе на расстояние. При этом совершится работа: На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: Пусть проводник l переместится параллельно самому себе на расстояние. При этом совершится работа:  Итак: Итак:  Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции. Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока,сцепленного с этим контуром. Рассмотрим прямоугольный контур с током 1-2-3-4-1 Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции. Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока,сцепленного с этим контуром. Рассмотрим прямоугольный контур с током 1-2-3-4-1  (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток, пронизывающий контур, направлен по нормали n к контуру, поэтому. Рис. 2.18 Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком. Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком. Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура: (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток, пронизывающий контур, направлен по нормали n к контуру, поэтому. Рис. 2.18 Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком. Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком. Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:  , где, равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку). , где, равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).  Провод 1–2 перерезает поток Провод 1–2 перерезает поток  , но движется против сил действия магнитного поля. , но движется против сил действия магнитного поля.  Тогда общая работа по перемещению контура: Тогда общая работа по перемещению контура:  или или  здесь здесь  – это изменение магнитного потока, сцепленного с контуром. – это изменение магнитного потока, сцепленного с контуром.
|



 .Элемент тока — векторная величина, равная произведению тока проводимости вдоль линейного проводника и бесконечно малого отрезка этого проводника.
.Элемент тока — векторная величина, равная произведению тока проводимости вдоль линейного проводника и бесконечно малого отрезка этого проводника.  .Примечание. Элемент тока имеет направление, совпадающее с направлением этого отрезка.Закон Био—Савара—Лапласа — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.
.Примечание. Элемент тока имеет направление, совпадающее с направлением этого отрезка.Закон Био—Савара—Лапласа — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.


 где Bn=В cos a — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos a (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено: оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции ФB через произвольную поверхность S
где Bn=В cos a — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos a (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено: оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции ФB через произвольную поверхность S  Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, Bn=B=const и
Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, Bn=B=const и 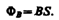 Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл×м2). Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:
Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл×м2). Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: 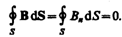 Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные. В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью m, согласно, равна
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные. В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью m, согласно, равна 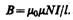 Магнитный поток сквозь один виток соленоида площадью S равен а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,
Магнитный поток сквозь один виток соленоида площадью S равен а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,  . Магнитный момент контура с током. Контур с током в магнитном поле. Опыт показывает, что электрические токи взаимодействуют между собой, напрмер, токи I притягиваются, а токи отталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром. Ориентацию его в пространстве характеризует направление нормали n(вектор) к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали n(вектор) (см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении.
. Магнитный момент контура с током. Контур с током в магнитном поле. Опыт показывает, что электрические токи взаимодействуют между собой, напрмер, токи I притягиваются, а токи отталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром. Ориентацию его в пространстве характеризует направление нормали n(вектор) к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали n(вектор) (см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении.  Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна IS, т.е. Mmax ~ IS, где I -ток контуре, S - площадь контура с током, (рис. 1). Векторную величину
Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна IS, т.е. Mmax ~ IS, где I -ток контуре, S - площадь контура с током, (рис. 1). Векторную величину  (1) называют магнитным моментом контура, который в СИ измеряется в А×м2. На пробные контуры с разными рm, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты М, но отношение Мmax/pm будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией В = Мmax/pm Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно установившегося во внешнем магнитном поле(см.рис.2) Поле вектора В можно представить с помощью силовых линий, (см. рис. 2), как и поле вектора таким образом В является аналогом Е.Магнитная индукция в СИ измеряется в теслах: 1 Тл=1 Нм/1 А×м2. Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 А м2, действует максимальный вращающий момент, равный 1 Нм. На контур с током, помещенный в магнитное поле с индукцией действует вращающий момент
(1) называют магнитным моментом контура, который в СИ измеряется в А×м2. На пробные контуры с разными рm, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты М, но отношение Мmax/pm будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией В = Мmax/pm Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно установившегося во внешнем магнитном поле(см.рис.2) Поле вектора В можно представить с помощью силовых линий, (см. рис. 2), как и поле вектора таким образом В является аналогом Е.Магнитная индукция в СИ измеряется в теслах: 1 Тл=1 Нм/1 А×м2. Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 А м2, действует максимальный вращающий момент, равный 1 Нм. На контур с током, помещенный в магнитное поле с индукцией действует вращающий момент  Величина его M =.
Величина его M =.  Работа по перемещению проводника и контура с током в магнитном поле. Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле В,перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор В сонаправлен с n.
Работа по перемещению проводника и контура с током в магнитном поле. Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле В,перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор В сонаправлен с n.  На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: Пусть проводник l переместится параллельно самому себе на расстояние. При этом совершится работа:
На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: Пусть проводник l переместится параллельно самому себе на расстояние. При этом совершится работа:  Итак:
Итак:  Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции. Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока,сцепленного с этим контуром. Рассмотрим прямоугольный контур с током 1-2-3-4-1
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции. Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока,сцепленного с этим контуром. Рассмотрим прямоугольный контур с током 1-2-3-4-1  (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток, пронизывающий контур, направлен по нормали n к контуру, поэтому. Рис. 2.18 Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком. Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком. Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
(рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток, пронизывающий контур, направлен по нормали n к контуру, поэтому. Рис. 2.18 Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком. Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком. Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:  , где, равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).
, где, равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).  Провод 1–2 перерезает поток
Провод 1–2 перерезает поток  , но движется против сил действия магнитного поля.
, но движется против сил действия магнитного поля.  Тогда общая работа по перемещению контура:
Тогда общая работа по перемещению контура:  или
или  здесь
здесь  – это изменение магнитного потока, сцепленного с контуром.
– это изменение магнитного потока, сцепленного с контуром.


