
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение динамики вращательного движения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Билет1. Основное уравнение динамики вращательного движения.
второй закон Ньютона для вращательного движения Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела Световая волна. Интерференция световых волн. Свет — в физической оптике электромагнитное излучение, воспринимаемое человеческим глазом. В качестве коротковолновой границы спектрального диапазона, занимаемого светом, принят участок сдлинами волн в вакууме 380—400 нм (750—790 ТГц), а в качестве длинноволновой границы — участок 760—780 нм (385—395 ТГц)[1].В широком смысле, используемом вне физической оптики, светом часто называ
Билет2 Билет №3 1. Кинематика вращательного движения. Связь между векторами v и ω. вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси. Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта: Единица измерения угловой скорости радиан в секунду (рад/с).
/////////////
При равномерном вращении его можно охарактеризовать периодом вращения Т – временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π: /////////////////
….....................
Для характеристики неравномерного вращения тела вводится понятие углового ускорения. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: ////////////////////////(1.20)
Таблица 1.1
2. Уравнения Максвелла. 06 • Первую пару уравнений Максвелла образуют ///// • Первое из этих уравнений связывает значения Е с временными изменениями вектора В и является по существу выражением закона электромагнитной индукции. Второе уравнение отражает то свойство вектора В, что его линии замкнуты (или уходят в бесконечность) ////////// Билет №4 Билет №5 Работа. Мощность. Работой называется скалярная величина, равная произведению проекции силы на направление перемещения и пути s,проходимого точкой приложения силы A fs cos (1.53)Если сила и направление перемещения образуют острый угол (cosα>0), работа положительна. Если угол α – тупой (cosα<0),работа отрицательна. При α = π/2 работаравна нулю
Мощность W есть величина, равная отношению работы ΔА к промежутку времени Δt, за который она совершается://///////////////////// Если работа меняется со временем, то вводится мгновенное значение мощности://///////// Билет №6 Уравнения Максвелла. 2. Дифракция Френеля от простейших преград. Билет №7 Билет№8 Билет №9 В состоянии равновесия сила mg уравновешива ется упругой силой k Δ l0: mg k l 0 (1.129) 0 f mg k ( l x) f kx (1.130) • Силы такого вида принято Называть квазиупругими Амплитудой колебания. • Величина, стоящая в скобках под знаком Начальной фазой колебания. • промежуток времени Т, за который фаза колебания получает приращение, равное 2π Циклической частотой. 0 2 (1.139) Энергия гармонического Колебания • Продифференцировав (1.135) по времени, Совпадает со средним значением Ep и равно Е/ 2. Ток индукционным. • Величина индукционного тока определяется лишь скоростью изменения Φ, т. е. значением производной d Φ/ d t. При изменении знака Тока. Явление электромагнитной Индукции. • Привило Ленца гласит, что индукционный ток всегда Его вызывающей. Билет№10 Нуль …... • Разделив это выражение на L и заменив через (2.187) (2.188); (2.189) Ююю • Заменяя ω0 по формуле (2.188), получим (2.194) Свободные затухающие Колебания. • Уравнение колебаний можно получить, исходя из того, Т. е. …. (2.197) имеет вид: (2.198) где …. Подставляя значение (2.188) для ω0 и (2.196) для β, Находим, что (2.199) • Разделив (2.198) на емкость С, получим напряжение на конденсаторе: (2.200) Билет№12 Сила Лоренца равна …. Таким образом, движение Радиус окружности, по Которой происходит вращение Определяется формулой (2.184) с заменой v на v = v sinα. • Шаг спирали l можно найти, умножив v ║ на определяемый Формулой (2.185) период обращения Т: …............ 2. Поляризация при двойном лучепреломлении. Двойно́е лучепреломле́ние — эффект расщепления в анизотропных средах луча света на две составляющие. Впервые обнаружен датским ученымРасмусом Бартолином на кристалле исландского шпата. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным (o — ordinary), второй же отклоняется в сторону, и называется необыкновенным (e — extraordinary). Направление колебания вектора электрического поля необыкновенного луча лежит в плоскости главного сечения (плоскости, проходящей через луч и оптическую ось кристалла). Оптическая ось кристалла — направление в оптически анизотропном кристалле, по которому луч света распространяется, не испытывая двойного лучепреломления. Нарушение закона преломления света необыкновенным лучом связанно с тем, что скорость распространения света (а значит и показатель преломления) волн с такой поляризацией, как у необыкновенного луча, зависит от направления. Для обыкновенной волны скорость распространения одинакова во всех направлениях. Можно подобрать условия, при которых обыкновенный и необыкновенный лучи распространяются по одной траектории, но с разными скоростями. Тогда наблюдается эффект изменения поляризации. Например, линейно поляризованный свет, падающий на пластинку можно представить в виде двух составляющих (обыкновенной и необыкновенной волн), двигающихся с разными скоростями. Из-за разности скоростей этих двух составляющих, на выходе из кристалла между ними будет некоторая разность фаз, и в зависимости от этой разности свет на выходе будет иметь разные поляризации. Если толщина пластинки такова, что на выходе из неё один луч на четверть волны (четверть периода) отстаёт от другого, то поляризация превратится в круговую (такая пластинка называется четвертьволновой), если один луч от другого отстанет на пол волны, то свет останется линейно поляризованным, но плоскость поляризации повернётся на некоторый угол, значение которого зависит от угла между плоскостью поляризации падающего луча и плоскостью главного сечения (такая пластинка называется полуволновой).Качественно явление можно объяснить следующим образом. Из уравнений Максвелла для материальной среды следует, что фазовая скорость света в среде обратно пропорциональна величине диэлектрической проницаемостиε среды. В некоторых кристаллах диэлектрическая проницаемость — тензорная величина — зависит от направления электрического вектора, то есть от состояния поляризации волны, поэтому и фазовая скорость волны будет зависеть от ее поляризации. Согласно классической теории света, возникновение эффекта связано с тем, что переменное электромагнитное поле света заставляет колебаться электроны вещества, и эти колебания влияют на распространение света в среде, а в некоторых веществах заставить электроны колебаться проще в некоторых определённых направлениях.Искусственное двойное лучепреломление. Помимо кристаллов двойное лучепреломление наблюдается и визотропных средах, помещённых в электрическое поле (эффект Керра), в магнитное поле (эффект Коттона — Мутона, эффект Фарадея), под действием механических напряжений (фотоупругость). Под действием этих факторов изначально изотропная среда меняет свои свойства и становится анизотропной. В этих случаях оптическая ось среды совпадает с направлением электрического поля, магнитного поля, направлением приложения силы.Отрицательные кристаллы — одноосные кристаллы, в которых скорость распространения обыкновенного луча света меньше, чем скорость распространения необыкновенного луча. В кристаллографии Отрицательными кристаллами называют также жидкие включения в кристаллах, имеющие ту же форму, что и сам кристалл.Положительные кристаллы — одноосные кристаллы, в которых скорость распространения обыкновенного луча света больше, чем скорость распространения необыкновенного луча. Билет№13 Излучение диполя.06 Называется элементарным • Дипольный электрический Момент такой системы равен p ql cos t n p m cos t, (2.228) • где l – удвоенная амплитуда Ленный вдоль оси диполя, p m = ql n • Волновой фронт в так называемой волновой зоне, т. е. Зависимость Интенсивности волны от угла θ изображается с Помощью диаграммы Направленности диполя (рис. 246). • Энергия, излучаемая по всем направлениям в Излучения. (2.230) Билет№14 Данной точке. Отрицателен Осью диполя. Найдем напряжен- Ность поля на оси Диполя, а также на Прямой, проходя- Щей через центр Диполя и перпен- Дикулярной к его оси (рис. 4). • Положение точек Будем характеризо- Вать их расстояни- ем r от центра дипо- ля. Напомним, что r >> l. На оси диполя векторы Е+ и Е– имеют противополож- Следует, что …......... Билет№15 Энергия • Физическая величина, характеризующая Скоростью и, • во-вторых, нахождением тела в Потенциальном поле сил. • Энергия первого вида называется Вектора v. (1.64) (1.65) Умножив на m числитель и знаменатель, уравнение (1.65) можно переписать как: (1.66) Кинетической энергии ….......... A T 2 T1 (1.67) Потенциальная энергия (1.68) Тел, образующих систему …........... Закон сохранения энергии E E 2 E 1 A н. к. (1.72) Для системы из N тел, между которыми Линия напряженности. Поток вектора напряженности • Густота линий выбирается так, чтобы количество Вектора Е. • Линии Е точечного заряда представляют собой радиальные прямые. ….. • Следовательно, полное число линий N равно (2.12) Если площадка dS ориентирована так, что нормаль к ней образует с вектором Е угол α, то количество Нормали к площадке численно равно ….......... • где выражение для Ф называется потоком вектора Е В тех местах, где вектор Е Объем, охватываемых поверх- ностью), Еn и соответственно d Ф будут отрицательны (рис. 10) Теорема Гаусса • Можно показать, что, как и для сферической Билет№16 Изменения. Инерциальные системы Отсчета • Система отсчета, в которой выполняется Неинерциальной. • Примером инерциальной системы Инерциальной Групповая скорость — это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Групповая скорость во многих важных случаях определяет скорость переноса энергии и информации квазисинусоидальной волной (хотя это утверждение в общем случае требует серьёзных уточнений и оговорок). Групповая скорость определяется динамикой физической системы, в которой распространяется волна (конкретной среды, конкретного поля итп). В большинстве случаев подразумевается линейность этой системы (точно или приближенно). Для одномерных волн групповая скорость вычисляется из закона дисперсии:
где Групповая скорость волн в пространстве (например, трехмерном или двумерном) определяется градиентомчастоты по волновому вектору
Замечание: групповая скорость вообще говоря зависит от волнового вектора (в одномерном случае - от волнового числа), то есть вообще говоря различна для разной величины и для разных направлений волнового вектора. Билет№17 Работа сил Электростатического поля …....... …........ …........ • мы учли, что …..... • Отсюда для работы на пути 1–2 получаем (2.23) • Следовательно, силы, действующие на заряд q' в поле неподвижного заряда q, являются потенциальными. ….... • где El – проекция вектора Е на направление элементарного перемещения d l Циркуляцией по контуру. • Таким образом, для электростатического Потенциал. • Для разных пробных значений q′ отношение Wp/qпр будет постоянным (2.25) (2.26) • ведичина φ ─ называется потенциалом поля Электрических полей Из 225 и226 получаем С учетом (2.23) получаем …....... Для потенциальной энергии заряда q′ в поле Отдельности Из 226 вытекает что Средах Однородном веществе Примеры мутных сред: – дым (мельчайшие твердые частицы в газе) – туман (капли жидкости в воздухе, газе) – суспензия клеток – эмульсия (дисперсная система, состоящая из Другие виды энергии Поглощающего вещества …....... …........ …..... Билет№18 Второй закон Ньютона.02 Тела. Связь между напряженностью Направление r равна Можно написать Щении вдоль касательной к поверхности τ на величину d τ Потенциал не изменится, так что φ/τ = 0. Но φ/τ равна Циальной поверхности будет Совпадать с направлением Же точке. Билет№19 Конденсаторы • Под емкостью конденсатора понимается физическая величина, пропорциональная заряду q и обратно Соединение конденсаторов • При параллельном соединении (рис. 50) на каждой из Напряжение Обкладках. • Поэтому напряжение на каждом из конденсаторов: Закон Кирхгофа. Билет№20 Можно придать другой вид ….............. Векторную величину p m v (1.44) Закон сохранения импульса • Импульсом системы р называется Образующих систему, ….................... Центром тяжести системы. • Скорость центра инерции получается путем дифференцирования r с по времени: ................. Учитывая, что mi vi есть рi, а Σрi дает импульс системы р, можно написать p m v c(1.50) Таким образом, импульс системы равен Каждой из внутренних сил По третьему закону Ньютона можно написать f ij = – f ji • Символом F i обозначена Результирующая внешних сил, действующая на тело i Уравнение (1.45) …...... …......... ….......... Нулю, вследствие чего Р постоянен Постоянным p m v c (1.50) Энергия системы зарядов.02 Рассмотрим систему из двух точечных зарядов q 1 и q 2, находящихся на расстоянии r 12. • Работа переноса заряда q 1 из бесконечности в точку, удаленную от q 2 на r 12 равна: где φ 1 – потенциал, создаваемый зарядом q 2 в той точке, в которую перемещается заряд q 1 • Аналогично для второго заряда получим: …........ Равна энергии трех зарядов …............... …..................... где φ1 – потенциал, создаваемый зарядами q 2 и q 3 в той точке, где расположен заряд q 1 и т. д. Добавляя к системе зарядов последовательно q 4, q 5 и т. д., можно убедиться в том, что в случае N зарядов потенциальная энергия Системы равна где φi – потенциал, создаваемый в той точке, где находится qi, всеми зарядами, кроме i -го. Билет№21 Сила (2.147) Выражение (2.147) совпадает с (2.104), если положить k = 1. Следовательно, в СИ закон Ампера имеет вид d f i d lB (2.148) df iB dl sin (2.149) Сила Лоренца • Согласно (2.148) на элемент тока d l действует в магнитном поле сила d f i d lB (2.150) • Заменив id l через S j dl [см. (2.111)], выражению закона Ампера можно придать вид d f Sdl jB jB dV • где dV – объем проводника, к которому приложена сила d f. • Разделив d f на dV, получим «плотность силы», т. е. силу, действующую на единицу объема проводника: f ед. об jB (2.151) Найдем, что fед. об ne 'uB • Эта сила равна сумме сил, приложенных к носителям в единице объема. Таких носителей n, следователь- Важно отметить, что закон говорит только об общей излучаемой энергии. Распределение энергии по спектруизлучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина. Зако́н смеще́ния Ви́на даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела. λmax = b / T ≈ 0,002898 м·К × T −1 (K), где T — температура, а λmax — длина волны с максимальной интенсивностью. Коэффициент b, называемыйпостоянной Вина, в системе СИ имеет значение 0,002898 м·К. Для частоты света
Где α ≈ 2,821439… — постоянная величина (корень уравнения k — постоянная Больцмана, h — постоянная Планка, T — температура (в кельвинах). Билет№22 Третий закон Ньютона. Направлению. f12 f21 (1.42) Билет№23 Формула Планка. Билет№24 Билет№25 Закон Джоуля – Ленца. Фотоэффект. Билет№26 Эффект Комптона.
Билет1. Основное уравнение динамики вращательного движения.
второй закон Ньютона для вращательного движения Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 9917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.011 с.) |

 Это основное уравнение динамики вращательного движения тела: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично по форме записи выражению второго закона Ньютона для поступательного движения тела.
Это основное уравнение динамики вращательного движения тела: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично по форме записи выражению второго закона Ньютона для поступательного движения тела. По определению угловое ускорение
По определению угловое ускорение  и тогда это уравнение можнопереписать следующим образом
и тогда это уравнение можнопереписать следующим образом  с учетом (5.9)
с учетом (5.9)  или
или 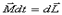
 , равно импульсу момента
, равно импульсу момента  всех внешних сил, действующих на это тело.
всех внешних сил, действующих на это тело.
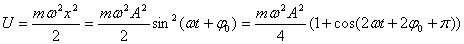





 ////////////////(1.21)
////////////////(1.21) ////////////////////////////
////////////////////////////
 Скалярное произведение двух векторов равно:AB AB cos.Выражение для работы (1.54) можно записать в виде скалярного произведения
Скалярное произведение двух векторов равно:AB AB cos.Выражение для работы (1.54) можно записать в виде скалярного произведения где под Δs подразумевается вектор элементарного перемещения, который мы ранее обозначали через Δr. s v t ////////////
где под Δs подразумевается вектор элементарного перемещения, который мы ранее обозначали через Δr. s v t //////////// ,
, — угловая частота,
— угловая частота,  — волновое число.
— волновое число. :
:
 (в герцах) закон смещения Вина имеет вид:
(в герцах) закон смещения Вина имеет вид:
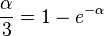 ),
), 


