Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон динамики. Уравнение моментов для тела движущего по окружностиСодержание книги
Поиск на нашем сайте
Пусть точка движется по окружности радиуса с центром в т. О под действием силы F, составляющей угол a с касательной а окружности (рис. 26).
Учитывая, что и умножив обе части (61) на R получим:
из рисунка видно, что Rcosa=h (плечо силы относительно центра окружности). Учитывая также направление векторов углового ускорения и момента силы относительно центра окружности, получим: Сравним полученное выражение с основным законом динамики Ньютона в частной формулировке
Заметим, что в (63) и (64) физический смысл аналогичен, только речь идет о разных типах движения. Поэтому одинаков и физический смысл величин m и mR2. Следовательно, величина mR2 определяет инертные свойства тела при вращательном движении. Эта величина I=mR2 называется моментом инерции тела (точки). С учетом сказанного основной закон динамики для вращательного движения записывают в виде:
Уравнение моментов относительно произвольного центра.
где r – радиус-вектор вращающейся материальной точки. Основной закон динамики вращательного движения (уравнение моментов) относительно произвольного центра будем находить в виде, аналогичном (66).
 Учитывая (67), получим: Учитывая (67), получим:
Отметим, что:
Тогда:
 Очевидно, что первый член в правой части равенства равен нулю, а второй - моменту силы относительно выбранного центра. Следовательно: Очевидно, что первый член в правой части равенства равен нулю, а второй - моменту силы относительно выбранного центра. Следовательно:
Уравнение моментов относительно координатных осей. Совершенно аналогично можно получить уравнения моментов относительно координатных осей:
4.16. движение тел в поле центральных сил.
Центральными называют силы, линии действия которых проходят в своё время через один и тот же центр. Примером таких сил могут служить силы гравитационного взаимодействия между планетами Солнечной системы.
   Основные особенности движения тел в поле центральных сил рассмотрим на примере движения планеты вокруг Солнца. Планета Р (рис.27) движется вокруг Солнца, центр масс которого находится в точке с. Радиус-вектор планеты, а сила, действующая на неё со стороны Солнца -. Движение планеты вокруг Солнца описывается уравнением моментов: Основные особенности движения тел в поле центральных сил рассмотрим на примере движения планеты вокруг Солнца. Планета Р (рис.27) движется вокруг Солнца, центр масс которого находится в точке с. Радиус-вектор планеты, а сила, действующая на неё со стороны Солнца -. Движение планеты вокруг Солнца описывается уравнением моментов:
Т.к.., следовательно:

Из условия постоянства модуля вектора следует, что:
Из рисунка видно, что h*dS равно удвоенной площади, ометаемой радиус-вектором планеты за промежуток времени dt. Обозначив эту площадь dσ, получим:
т.е. площадь, ометаемая радиус-вектором планеты в единицу времени (секториальная скорость) постоянна.
Основные законы динамики систем материальных точек. Система материальных точек.
Системой материальных точек (механической системой) называют совокупность взаимодействующих между собой точек, в которой положение и движение каждой из них зависит от положения и движения остальных точек системы (например, Солнечная планетная система). Система точек характеризуется совокупностью сил, приложенных ко всем точкам смстемы как со стороны других точек системы (внутренние силы), так и со стороны тел, не входящих в состав данной системы (внешние силы). Характеристикой системы является её масса, равная сумме масс точек, входящих в состав системы. Кроме того, система характеризуется положением её центра масс, которое можно задавать векторным и координатным способами:
 
где: ― масса k-й точки системы, ― её радиус-вектор, ― её координаты, - радиус-вектор центра масс системы, ― его координаты.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.72 (0.01 с.) |

 (рис 26)
(рис 26) Второй закон динамики в проекциях на касательное направление имеет вид:
Второй закон динамики в проекциях на касательное направление имеет вид:


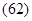







 Основной закон динамики в общей формулировке можно записать в виде:
Основной закон динамики в общей формулировке можно записать в виде:
 При вращательном движении вокруг центра О роль импульса играет момент импульса относительно центра:
При вращательном движении вокруг центра О роль импульса играет момент импульса относительно центра:






 Следовательно:
Следовательно:
 Подобным же образом получаем:
Подобным же образом получаем: