
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал.Содержание книги
Поиск на нашем сайте
Потенциальная энергия взаимодействия численно равна работе сил взаимодействия по перемещению взаимодействующего тела из данного положения в бесконечность:
Энергетической характеристикой поля является гравитационный потенциал, равный потенциальной энергии единичной пробной массы, помещённой в данную точку поля:
Связь напряжённости и потенциала поля. На расстояниях
В этих же точках определим потенциалы:
Изменение потенциала на еденицу длинны:
Если точки расположены бесконечно близко друг к другу, связь напряжённости и потенциала принимает вид:
Зависимость веса тела от высоты. Для небольших высот (малы по сравнению с радиусом Земли) вес тела:
Где Гравитационное взаимодействие между телами конечных размеров. Взаимодействие между материальной точкой и тонким кольцом.
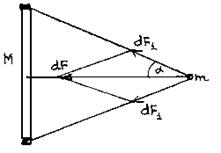
Материальная точка массы Равнодействующая сила взаимодействия с двумя выделенными элементами направлена к центру кольца и равна: Полную силу взаимодействия можно получить, интегрируя (225):
Рис.52
12.5.2. Взаимодействие точки с тонким сферическим слоем.
Пусть точечная пробная масса
Рис.53 Выделим в слое тонкое кольцо, радиус которого виден из центра слоя под углом
где:
масса кольца. Таким образом:
Перейдем в 226 к одной переменной:
откуда:
Сила взаимодействия со всем слоем, если точка находится за его пределами равна:
Если же точка находится внутри слоя, сила взаимодействия равна:
Взаимодействие между точечной массой и однородным шаром.
Точка массы
По (231) сила взаимодействия точки с выделенным слоем равна:
Интегрируя, получаем силу взаимодействия точки с шаром:
Если же точка находится внутри шара, надо учитывать взаимодействие только со слоями шара, с внутренними по отношению к точке:
где:
Отсюда сила взаимодействия равна:
Работа и энергия. Работа силы, работа суммы сил. Работой силы называют величину, равную произведение силы на перемещение точки приложения силы:
Как видно, если сила и перемещение взаимно перпендикулярны, работа силы равна нулю. Например, центростремительная сила не производит работы, ее роль сводится лишь к искривлению траектории. Работа суммы сил равна сумме работ, производимых отдельными силами системы. Например:
Частные случаи вычисления работы. Работа силы тяжести.
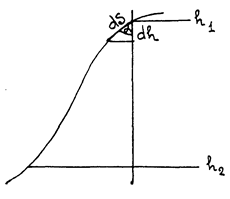
Рис.54 Пусть тело под действием силы тяжести скользит по наклонной поверхности произвольной формы (рис.54.) работа нормальной реакции по (235) равна нулю, поэтому при отсутствии трения работу совершает только сила тяжести. На элементарном перемещении работа
Следовательно, на конечном перемещении работа сил тяжести не зависит от формы траектории и равна:
где: Работа упругих сил.
На гладкой горизонтальной плоскости находится тело, скрепленное пружиной жесткости
Рис.55 Если под действие внешней силы
Работа же силы на конечном перемещении:
где
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.172.9 (0.006 с.) |

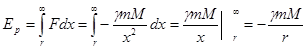 (220)
(220)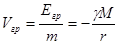 (221)
(221) и
и 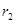 от источника поля напряжённости поля равны:
от источника поля напряжённости поля равны:
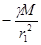 и
и 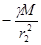
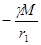 и
и 
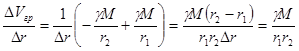
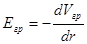 (222)
(222)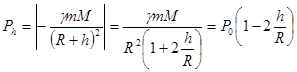 (223)
(223)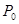 - вес тела на поверхности Земли.
- вес тела на поверхности Земли. находится на расстоянии
находится на расстоянии  от тонкого кольца массы
от тонкого кольца массы 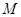 (рис.52). Выделим два элемента кольца массы
(рис.52). Выделим два элемента кольца массы 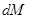 , расположенные на концах расположенные под углом
, расположенные на концах расположенные под углом 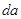 из его центра. По закону всемирного тяготения сила взаимодействия
из его центра. По закону всемирного тяготения сила взаимодействия 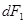 между точкой и каждым из элементов равна:
между точкой и каждым из элементов равна: 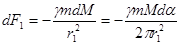 (224)
(224)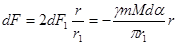 (225)
(225)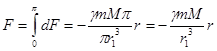 (226)
(226)
 и массы
и массы 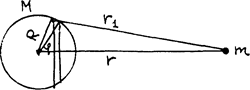
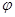 , а поперечный размер (ширина кольца) – под уuлом
, а поперечный размер (ширина кольца) – под уuлом 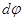 . По (226) сила взаимодействия между точкой и выделенным кольцом равна:
. По (226) сила взаимодействия между точкой и выделенным кольцом равна: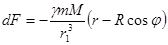 (227)
(227)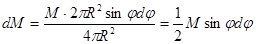
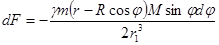 (228)
(228)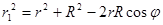
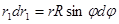
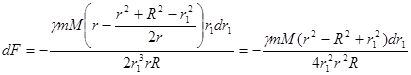 (229)
(229)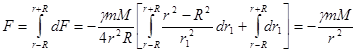 (230)
(230)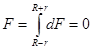 (231)
(231) и толщины
и толщины  с центром в центре шара. Масса выделенного слоя равна:
с центром в центре шара. Масса выделенного слоя равна: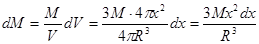
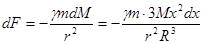
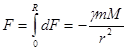 (232)
(232)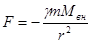 (233)
(233)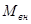 - суммарная масса внутренних слоев шара, равная:
- суммарная масса внутренних слоев шара, равная: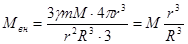
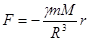 (234)
(234)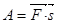 (235)
(235)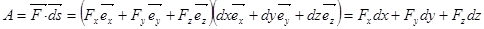 (236)
(236)
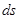 силы равна:
силы равна: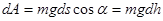 (237)
(237)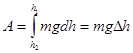
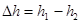 перемещение тела по вертикали.
перемещение тела по вертикали. с вертикальной стенкой (рис.55).
с вертикальной стенкой (рис.55).
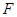 пружина растягивается на
пружина растягивается на 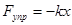 . Элементарная работа упругих сил по перемещению тела из этого положения на
. Элементарная работа упругих сил по перемещению тела из этого положения на 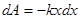
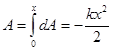 (238)
(238)


