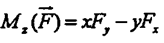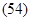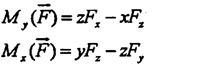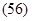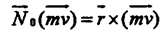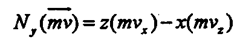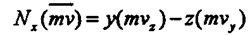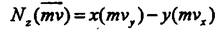Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Й закон динамики (закон действия и противодействия).Содержание книги
Поиск на нашем сайте Существует две равноправные формулировки 3-го закона: 1. Действию всегда есть равное и противоположно направленное противодействие 2. Тела действуют друг на друга с силами, равными по величине и противоположно направленными. Эти формулировки получены в результате обобщения экспериментальных фактов, которые свидетельствуют о том, что тела взаимодействуют всегда попарно, т.е. на изолированное тело силы не действуют. С 3-м законом динамики тесно связан закон сохранения импульса. Действительно, если на два тела действуют только силы взаимодействия между ними, то, по 3-му закону динамики, эти силы равны по величине и противоположно направлены. Следовательно, по основному закону, одинаковы и противоположно направлены изменения импульсов тел, а общий импульс системы тел не изменяется.
ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ. Если на тело действует несколько сил, то каждая из них сообщает телу ускорение, определяемое основным законом динамики, так, как если бы других сил не было.
где ex, ey, ez - орты прямоугольной системы координат OXYz. Второй закон динамики в этом случае имеет вид:
откуда:
Т. о., в приведенном рассуждении учтен принцип независимости действия сил. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОГО ЦЕНТРА. Моментом силы называют количественную меру вращательного эффекта, вызываемого силой. Момент силы должен определять величину этого эффекта, плоскость поворота точки и направление поворота в этой плоскости.
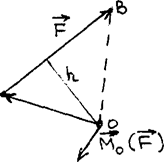
Величина момента силы равна произведению модуля силы на ее плечо h (величину перпендикуляра, опущенного из заданного центра O на линию действия силы). Если начало вектора силы совпадает с точкой А, а конец – А с точкой В, то, очевидно, плоскость поворота совпадает с плоскостью треугольника OAB (рис. 23).
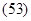 Очевидно, что такой вектор равен векторному произведению: Очевидно, что такой вектор равен векторному произведению:
где: r - радиус-вектор точки приложения силы, проведенный из заданного центра. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ.
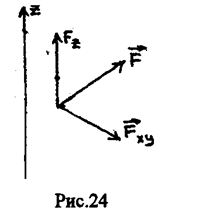
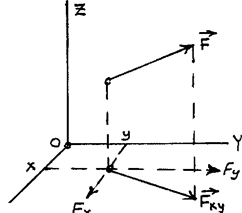
Моментом силы относительно оси называют величину, характеризующую вращательный эффект, вызываемый силой при вращении тела вокруг заданной оси. К телу А, способному вращаться вокруг оси z приложена сила F (рис. 24). Очевидно, что эффект вызываемый силой, определяется суммой эффектов, вызываемых ее проекциями Fz и Fxy, первая из которых вращения тела вокруг оси z вызвать не может. Следовательно, момент силы относительно заданной оси определяется моментом ее проекции на плоскость, перпендикулярную оси, относительно точки Пересечения оси с плоскостью. МОМЕНТ СИЛЫ оТНОСИТЕЛЬНО КООРДИНАТНОЙ ОСИ. Пользуясь полученным выше результатом можно записать выражения моментов силы относительно координатных осей. Пусть к телу приложена сила F, координаты точки приложения которой равны x,y,z. Момент силы F относительно оси oz равен моменту ее проекции Fxy относительно начала координат (т. 0). В свою очередь момент Fxy равен сумме моментов сил Fx и Fy относительно того же центра. Очевидно, что плечи сил Fx и Fy численно равны координатам точки приложения силы y и x соответственно. С учетом знаков моментов этих составляющих можно записать
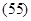 Аналогично определяются моменты силы F относительно осей ОХ и ОУ: Аналогично определяются моменты силы F относительно осей ОХ и ОУ:
МОМЕНТ СИЛЫ оТНОСИТЕЛЬНО ЦЕНТРА И КООРДИНАТНЫХ ОСЕЙ. Количественной мерой движения при вращении является момент количества движения (момент импульса). По аналогии с моментом силы момент импульса относительно центра и координатных осей записываются в виде:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |

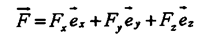 Например, произвольно направленную и в пространстве силу F можно представить в виде суммы ее составляющих (компонентов):
Например, произвольно направленную и в пространстве силу F можно представить в виде суммы ее составляющих (компонентов):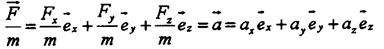
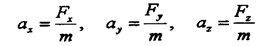
 (рис 23)
(рис 23)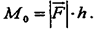 Условились вектор момента силы относительно центра M0(F) проводить из этого центра O перпендикулярно плоскости поворота в ту сторону, откуда поворот виден происходящим против хода часовых стрелок. Модуль же вектора (длина вектора в выбранном масштабе) равен.
Условились вектор момента силы относительно центра M0(F) проводить из этого центра O перпендикулярно плоскости поворота в ту сторону, откуда поворот виден происходящим против хода часовых стрелок. Модуль же вектора (длина вектора в выбранном масштабе) равен.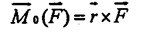
 (рис 25)
(рис 25)