
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение поперечных размеров тел.Содержание книги
Поиск на нашем сайте
Пусть две системы OXYZ и O'X'Y'Z' находятся в относительном движении. Одну из них, OXYZ, считаем неподвижной, другая же движется со скоростью v относительно первой так, что оси ОХ, 0'Х' и 0Z, О’Z' остаются параллельными, а ось О’Y' скользит вдоль оси OY. В подвижной системе вдоль оси O'Z' расположены "световые часы" (жесткий стержень с двумя зеркалами на концах, отражающими поверхностями друг к другу) так, что нижнее зеркало совпадает с началом системы отсчета (рис.34). В исходный момент, когда системы полностью совпадали, у нижнего зеркала произошла световая вспышка. Сигнал от нее достигает верхнего зеркала, отражается, приходит опять к нижнему зеркалу, и далее процесс повторяется периодически. Пусть по неподвижным часам промежуток
Рис.34 времени между вспышкой и приходом сигнала равен t. За это время в неподвижной системе световой сигнал проходит путь сt, а подвижная система - vt. Из рисунка видно, что длина световых часов, численно равная координате z верхнего зеркала, в неподвижной системе равна:
В подвижной системе, связанной с подвижными часами, длина их равна: z'=ct' (158) где: t ' - полупериод часов, т.е. промежуток времени между вспышкой и приходом сигнала к верхнему зеркалу. Учитывая эффект "замедления" хода времени, получаем:
т.е. поперечные размеры (по отношению к направлению движения) тел одинаковы в обеих системах отсчета: z'=z 8.6. Эффект "сокращения" длин.
Пусть теперь световые часы ориентированы вдоль оси подвижной системы так, что левое зеркало совпадает с ее началом. В исходный момент системы совпадали, и в этот момент у левого зеркала произошла вспышка. Сигнал от нее достигает правого зеркала через промежуток времени t1 по неподвижным часам (рис.35). Тогда:
где: l - длина световых часов, измеренная в неподвижной системе.
В подвижной системе период часов определяется соотношением:
где l' - длина часов, измеренная в подвижной системе. Отсюда:
Следовательно, продольные размеры тел в любой системе меньше собственных:
8.7. Преобразования Лоренца. Преобразования Лоренца дают связь между пространственными и временными координатами событий в двух инициальных системах отсчета, находящихся в относительном движении. Учитывая, что поперечные размеры тел одинаковы, получаем: z'=z (166) х'=x (167)
С другой стороны, это соотношение можно представить в виде:
Соотношения (166,167,168,170) называют преобразованиями Лоренца. 8.8. Интервал. Инвариантность интервала. Интервалом S между двумя событиями называют величину, квадрат которой равен:
где xi,yi,zi,ti - пространственные и временные координаты событий. Используя преобразования Лоренца, запишем интервал в подвижной системе отсчета:
Таким образом, интервал является инвариантом: S /2=S 2 (171)
пространственной частями интервала различают: 1.Времениподобные интервалы (cΔt > Δl). 2.Пространственноподобные интервалы (cΔt <s Δl). 3. Светоподобные интервалы (сΔt = Δl). 8.9. Преобразования компонентов вектора скорости. Преобразования компонентов вектора скорости можно получить, пользуясь преобразованиями Лоренца:
Релятивистская масса, релятивистский импульс.
Из факта предельности скорости света следует, что тела могут двигаться только со скоростями, меньшими скорости света. Если на тело действует постоянная сила, то его ускорение пропорционально силе лишь при малых скоростях. С ростом скорости при неизменной силе ускорение начинает уменьшаться, что можно объяснить только возрастанием массы тела с ростом скорости. Масса тела, движущегося со скоростью n, равна:
Соответственно, импульс тела определяется выражением:

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.9 (0.007 с.) |


 (157)
(157)


 После отражения сигнал и левое зеркало движутся навстречу друг другу и встречаются в момент времени t2 по неподвижным часам. Очевидно, что:
После отражения сигнал и левое зеркало движутся навстречу друг другу и встречаются в момент времени t2 по неподвижным часам. Очевидно, что: Период световых часов, измеренный в неподвижной системе, равен:
Период световых часов, измеренный в неподвижной системе, равен:

 (163)
(163)

 т.е.:
т.е.:


 Для сравнения координат у обратимся к предыдущему примеру:
Для сравнения координат у обратимся к предыдущему примеру:


 т.е.
т.е.




 В зависимости от соотношения между временной cΔt и -
В зависимости от соотношения между временной cΔt и -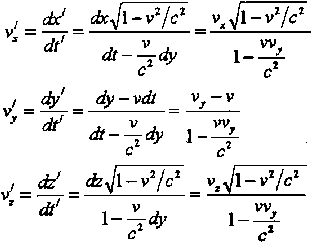





 Где, - масса тела в системе, связанной с ним, так называемая "масса покоя".
Где, - масса тела в системе, связанной с ним, так называемая "масса покоя".



