
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика тел переменной массы.Содержание книги
Поиск на нашем сайте
Телом переменной массы называют тело, масса которого с течением времени изменяется (M=M(t)) за счёт отделения от него или прибавления к нему дополнительной массы. Тело, от которого отделяется масса или к которому прибавляется масса, называется основным телом. Основной закон динамики тела переменной массы получим на примере ракеты.
6.1. Основной закон динамики тела переменной массы (уравнение Мещерского) для тела с убывающей массой.
 Пренебрегая величинами второго порядка малости, можем записать: Пренебрегая величинами второго порядка малости, можем записать:
направлена эта сила противоположно относительной скорости. Такую силу называют реактивной.
6.2. Основной закон динамики для тела с возрастающей массой.
Пренебрегая величинами второго порядка малости, преобразуем (94) к виду:
или
 где: ― относительная скорость добавляющейся массы. где: ― относительная скорость добавляющейся массы.
6.3. Первое соотношение Циолковского.
Первое соотношение Циолковского определяет скорость ракеты в конце активного участка траектории (того участка, на котором работает двигатель). Соотношение получим в предположении, что относительная скорость продуктов сгорания топлива u постоянная (1-я гипотеза Циолковского). Кроме того, будем считать, что ракета движется вне силовых полей.
или:
Постоянную интегрирования С определим из условий для начала активного участка, когда,а. Тогда:
Подставив в (98) найденное значение постоянной интегрирования, получаем:
 Таким образом, в любой точке активного участка траектории можно определить скорость ракеты v, зная её массу в этот момент. Отметим, что начальная масса ракеты состоит из массы корпуса и массы топлива, содержащегося в нём:. В конце активного участка топливо полностью сгорает, и масса ракеты определяется только массой её корпуса. Таким образом, в любой точке активного участка траектории можно определить скорость ракеты v, зная её массу в этот момент. Отметим, что начальная масса ракеты состоит из массы корпуса и массы топлива, содержащегося в нём:. В конце активного участка топливо полностью сгорает, и масса ракеты определяется только массой её корпуса.
Тогда скорость ракеты в конце активного участка траектории равна: Анализ полученного соотношения позволяет указать пути повышения скорости ракеты.
6.4. Второе соотношение Циолковского.
n+dn, и отделившихся продуктов сгорания массы –dM, двигавшихся со скоростью.
Полная работа, совершённая двигателем за промежуток времени dt, равна:
Абсолютная скорость продуктов сгорания топлива связана с относительной соотношением:
С учётом этого:
Используя соотношение Циолковского и полагая в нём, что скорость ракеты в начале активного участка траектории равна нулю, последнее соотношение приведём к одной переменной:
Полезная работа, совершённая двигателем за промежуток времени dt, равна:
Используя 1-е соотношение Циолковского, последнее равенство можно записать в виде:
Это дифференциальное выражение удобно интегрировать методом интегрирования «по частям», согласно которому:
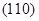 Полезная работа на всём активном участке траектории равна: Полезная работа на всём активном участке траектории равна:
Первый из интегралов интегрируем «по частям», полагая:
Тогда:
Согласно (109):
Подставив это значение в (110) получим:
По определению коэффициент полезного действия ракетного двигателя равен:
6.5. Линейный режим работы ракетного двигателя.
При линейном режиме работы ракетного двигателя масса ракеты уменьшается со временем по линейному закону:
где α определяет скорость сгорания топлива. При таком режиме массовый расход равен:
Таким образом, при линейном режиме реактивная сила постоянна, а ускорение ракеты и, соответственно, силы инерции, действующие на тела в корпусе ракеты со временем возрастают.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

 Предположим, что в момент времени t основное тело (корпус ракеты) имело массу М, двигалось со скоростью, а равнодействующая внешних приложенных к нему сил
Предположим, что в момент времени t основное тело (корпус ракеты) имело массу М, двигалось со скоростью, а равнодействующая внешних приложенных к нему сил
 равнялась. Через малый промежуток времени dt, т.е. в момент времени t+dt от основного тела отделилась масса –dM (dM<0), движущаяся со скоростью.
равнялась. Через малый промежуток времени dt, т.е. в момент времени t+dt от основного тела отделилась масса –dM (dM<0), движущаяся со скоростью. Основное тело в этот момент имеет массу M+dМ и движется со скоростью.
Основное тело в этот момент имеет массу M+dМ и движется со скоростью.
 Применим к системе «основное тело ― отделяющаяся масса» основной закон динамики для системы точек:
Применим к системе «основное тело ― отделяющаяся масса» основной закон динамики для системы точек: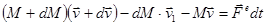
 Обозначив (скорость продуктов сгорания топлива относительно корпуса ракеты), получим основной закон динамики для тела с убывающей массой:
Обозначив (скорость продуктов сгорания топлива относительно корпуса ракеты), получим основной закон динамики для тела с убывающей массой: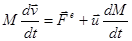



 От второго закона Ньютона выражение (93) отличается величиной, имеющей размерность силы. Учитывая, что dM<0, отметим, что при отделении массы от основного тела на него действует дополнительная сила, равная произведению массового расхода на относительную скорость, а
От второго закона Ньютона выражение (93) отличается величиной, имеющей размерность силы. Учитывая, что dM<0, отметим, что при отделении массы от основного тела на него действует дополнительная сила, равная произведению массового расхода на относительную скорость, а
 Предположим, что в момент времени t система состояла из основного тела массы М, двигавшегося со скоростью и малой массы dM, двигавшейся со скоростью. К моменту времени t+dt малая масса попадает на основное тело, т.е. система представляет уже собой одно тело массы M+dM, которое движется со скоростью. Если равнодействующая внешних сил, действующих на систему, равна, основной закон динамики записывается для системы в виде:
Предположим, что в момент времени t система состояла из основного тела массы М, двигавшегося со скоростью и малой массы dM, двигавшейся со скоростью. К моменту времени t+dt малая масса попадает на основное тело, т.е. система представляет уже собой одно тело массы M+dM, которое движется со скоростью. Если равнодействующая внешних сил, действующих на систему, равна, основной закон динамики записывается для системы в виде:


 Внешняя форма закона динамики для тела с возрастающей массой полностью совпадает с уравнением динамики для тела с убывающей массой. Разница в том, что на этот раз дополнительная сила совпадает по направлению с относительной скоростью, т.к. в случае добавляющейся массы dM>0.
Внешняя форма закона динамики для тела с возрастающей массой полностью совпадает с уравнением динамики для тела с убывающей массой. Разница в том, что на этот раз дополнительная сила совпадает по направлению с относительной скоростью, т.к. в случае добавляющейся массы dM>0. .Тогда в проекциях на направление движения ракеты уравнение Мещерского можно представить в виде:
.Тогда в проекциях на направление движения ракеты уравнение Мещерского можно представить в виде:



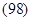 Интегрируя, получим:
Интегрируя, получим:








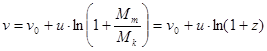


 Второе соотношение Циолковского определяет максимально возможный к.п.д. ракетного двигателя. По-прежнему считаем, что ракета движется вне силовых полей, а относительная скорость продуктов сгорания топлива постоянна. Кроме того, полагаем, что потерями на нагрев корпуса ракеты и на излучение можно пренебречь. При таких предположениях работа двигателя определяется изменением кинетической энергии системы «ракета ― отделившиеся продукты сгорания топлива». При этом полезная работа определяется изменением кинетической энергии только корпуса ракеты, а вся затраченная работа ― изменением кинетической энергии всей системы.
Второе соотношение Циолковского определяет максимально возможный к.п.д. ракетного двигателя. По-прежнему считаем, что ракета движется вне силовых полей, а относительная скорость продуктов сгорания топлива постоянна. Кроме того, полагаем, что потерями на нагрев корпуса ракеты и на излучение можно пренебречь. При таких предположениях работа двигателя определяется изменением кинетической энергии системы «ракета ― отделившиеся продукты сгорания топлива». При этом полезная работа определяется изменением кинетической энергии только корпуса ракеты, а вся затраченная работа ― изменением кинетической энергии всей системы. Положим, что в момент времени t масса ракеты была М, а скорость её n. В момент времени t+dt система состояла из одного тела массой M+dM, двигавшегося со скоростью
Положим, что в момент времени t масса ракеты была М, а скорость её n. В момент времени t+dt система состояла из одного тела массой M+dM, двигавшегося со скоростью

 Пренебрегая величинами второго и третьего порядка малости, получим:
Пренебрегая величинами второго и третьего порядка малости, получим:






 Интегрируя это равенство в пределах изменения массы ракеты (от до), получим значение полной работы, совершённой двигателем:
Интегрируя это равенство в пределах изменения массы ракеты (от до), получим значение полной работы, совершённой двигателем:







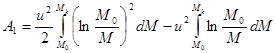








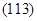



 Учитывая, что и, запишем окончательный вид второго соотношения Циолковского:
Учитывая, что и, запишем окончательный вид второго соотношения Циолковского:


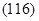

 т.е. со временем массовый расход не изменяется. Уравнение Мещерского при отсутствии внешних сил имеет вид:
т.е. со временем массовый расход не изменяется. Уравнение Мещерского при отсутствии внешних сил имеет вид:
 Очевидно, что реактивная сила со временем не изменяется. В то же время ускорение ракеты возрастает по закону:
Очевидно, что реактивная сила со временем не изменяется. В то же время ускорение ракеты возрастает по закону:



