
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение основного уравнения динамики вращательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Исследуйте зависимость углового ускорения диска от момента силы упругости нити, приводящего диск во вращение.
Оборудование: диск на оси из набора для изучения вращательного движения с двумя шкивами разного диаметра; блок; штатив; штангенциркуль; набор грузов; нить; секундомер.
Теоретические основы работы
Угловое ускорение вращающегося тела ε прямо пропорционально моменту сил М, под действием которого тело получает угловое ускорение:
Величина I, зависящая от свойств самого тела, называется моментом инерции. Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.
Моменты инерции однородных тел простейшей формы относительно некоторых осей
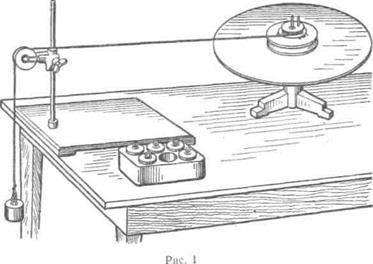
Для проверки этого уравнения, называемого основным уравнением динамики вращательного движения твердого тела, воспользуемся установкой, изображенной на рисунке 1.
На один из шкивов радиусом R намотаем нить. Нить перекинем через блок и к концу ее подвесим груз массой т. Момент М силы упругости F нити равен Модуль F силы упругости нити можно определить, применив для груза второй закон Ньютона:
В условиях работы ускорение а груза намного меньше ускорения свободного падения g (a << g). Следовательно, можно считать, что
Угловое ускорение ε по определению равно:
Так как в данном опыте начальная угловая скорость ω0 равна нулю, то
где ω0 – угловая скорость вращения диска, которую он приобретает за время t падения груза.
Порядок выполнения работы
Задание 1. Установите зависимость углового ускорения диска от действующей силы при постоянном плече этой силы. 1. Наматывая нить на верхний шкив радиусом R1, поднимите груз массой m1 = 0,1 кг на максимальную высоту. Отпустите груз и с помощью секундомера определите время t1 его падения. 2. После достижения грузом поверхности пола вычислите
После опускания груза на поверхность пола нить полностью должна сматываться со шкива диска. 3. Вычислите угловое ускорение ε1:
4. Повторив опыт с грузом массой m2 = 0,2 кг, вычислите угловую скорость ω2 и угловое ускорение ε2:
5. Результаты измерений и вычислений занесите в отчетную таблицу 1.
Отчетная таблица
6. Рассчитайте границы погрешностей измерений, сравните Задание 2. Исследуйте зависимость углового ускорения диска от плеча действующей силы. 1. Наматывая нить на шкив радиусом R2, поднимите груз массой m1 = 0,1 кг; отпустив его, определите время падения груза t3. 2. После достижения грузом поверхности пола вычислите угловую скорость вращения диска 3. Сравните отношения R1/R2 и ε1/ε3, сделайте вывод. (Значения R1 и ε1 получены при выполнении первого задания.) 4. Результаты измерений и вычислений занесите в таблицу 2.
Отчетная таблица 2
5. По результатам выполнения двух заданий сделайте общий вывод о зависимости углового ускорения диска от момента сил. Для этого сравните отношения угловых ускорений и соответствующих моментов сил.
Контрольные вопросы 1. Поясните принцип действия установки, с помощью которой проверяют основное уравнение динамики вращательного движения твердого тела. 2. Вычислите линейное ускорение движения груза и сравните его с ускорением свободного падения. Правильным ли было предположение, что в данной работе a << g? 3. Объясните причины неточного совпадения отношений
Творческий практикум
Используя данную установку, измерьте момент инерции диска
Лабораторная работа № 8
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.142 (0.009 с.) |


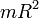



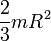


 .
.
 .
. и
и  .
.


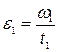


 и
и  сделайте вывод.
сделайте вывод. и угловое ускорение
и угловое ускорение 





