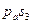Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ускорений точек звеньев и угловых ускорений звеньевСодержание книги
Поиск на нашем сайте
2.2.1.Определение ускорения точки А: Так как угловая скорость
Выбираем масштаб плана ускорений 2.2.2. Определение ускорения точки В: Запишем векторное уравнение: Вектор относительного ускорения Нормальное относительное ускорение равно: Найдём отрезок, изображающий вектор ускорения
Продолжаем строить план ускорений. Вектор ускорения Вектор ускорения Вектор ускорения
Нормальное ускорение равно: Найдём отрезок, изображающий вектор ускорения Продолжаем строить план ускорений. Вектор ускорения Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб
2.2.3. Определение ускорения точки C: Запишем векторное уравнение: Вектор относительного ускорения Нормальное относительное ускорение равно:
Найдём отрезок, изображающий вектор ускорения Вектор ускорения Вектор ускорения
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб
2.2.4. Определение ускорения точки S1:
2.2.5. Определение ускорения точки S2: Воспользуемся следствием из теоремы подобия. Составим пропорцию:
Данный отрезок откладываем на прямой ab от точки a. Точку s2 соединяем с полюсом pa. Величина ускорения: 2.2.6. Определение ускорения точки S3: Воспользуемся следствием из теоремы подобия. Составим пропорцию:
Данный отрезок откладываем на прямой pab от точки b. Точку s3 соединяем с полюсом pa. Величина ускорения: 2.2.7. Определение ускорения точки S4: Воспользуемся следствием из теоремы подобия. Составим пропорцию:
Данный отрезок откладываем на прямой bc от точки b. Точку s4 соединяем с полюсом pa. Величина ускорения: 2.2.8. Определение углового ускорения шатуна АВ:
Для определения направления 2.2.9. Определение углового ускорения коромысла ВO2:
Для определения направления 2.2.10. Определение углового ускорения шатуна ВС:
Для определения направления
Кинематическая схема механизма
План ускорений
Силовой расчет механизма
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.105 (0.007 с.) |

 является постоянной, то
является постоянной, то  .
. . Вектор ускорения
. Вектор ускорения  направлен параллельно кривошипу О1А от точки А к точке О1.
направлен параллельно кривошипу О1А от точки А к точке О1. . Найдём отрезок, изображающий вектор ускорения
. Найдём отрезок, изображающий вектор ускорения  . Из полюса плана ускорений pa откладываем данный отрезок в направлении, параллельном АО1.
. Из полюса плана ускорений pa откладываем данный отрезок в направлении, параллельном АО1.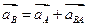 .
. раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие: 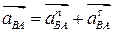 .
. .
. на плане:
на плане: .
. направлен перпендикулярно АВ. Проводим это направление из точки n плана ускорений.
направлен перпендикулярно АВ. Проводим это направление из точки n плана ускорений. раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие: .
. .
. на плане:
на плане:  .
. направлен параллельно ВO2. Откладываем отрезок
направлен параллельно ВO2. Откладываем отрезок  из точки
из точки  плана ускорений в указанном направлении от точки В к точке O2. Вектор ускорения
плана ускорений в указанном направлении от точки В к точке O2. Вектор ускорения  направлен перпендикулярно ВO2. Проводим это направление из точки m плана ускорений. Две прямые линии, проведённые из точек n и m в указанных направлениях, пересекаются в точке b.
направлен перпендикулярно ВO2. Проводим это направление из точки m плана ускорений. Две прямые линии, проведённые из точек n и m в указанных направлениях, пересекаются в точке b. , получим:
, получим: ;
; ;
; ;
; .
. .
. раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие: 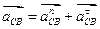 .
. .
. на плане:
на плане:  . Продолжаем строить план ускорений. Так как отрезок bk мал, то его на плане ускорений не откладываем. Точки b и k совпадают.
. Продолжаем строить план ускорений. Так как отрезок bk мал, то его на плане ускорений не откладываем. Точки b и k совпадают. направлен перпендикулярно ВС. Проводим это направление из точки k плана ускорений.
направлен перпендикулярно ВС. Проводим это направление из точки k плана ускорений. направлен параллельно оси X–X. Проводим это направление из полюса pa. Две прямые линии, проведённые из точек k и pa в указанных направлениях, пересекаются в точке c.
направлен параллельно оси X–X. Проводим это направление из полюса pa. Две прямые линии, проведённые из точек k и pa в указанных направлениях, пересекаются в точке c. ;
; ;
; .
. . Вектор ускорения
. Вектор ускорения  направлен параллельно кривошипу О1А от точки S1 к точке О1.
направлен параллельно кривошипу О1А от точки S1 к точке О1. ,
,  .
. .
. ,
,  .
. .
. ,
,  .
. .
. .
. переносим вектор
переносим вектор  в точку В шатуна АВ и смотрим, как она движется относительно точки А. Направление этого движения соответствует
в точку В шатуна АВ и смотрим, как она движется относительно точки А. Направление этого движения соответствует  .
. переносим вектор
переносим вектор  в точку В коромысла ВО2 и смотрим, как она движется относительно точки О2. Направление этого движения соответствует
в точку В коромысла ВО2 и смотрим, как она движется относительно точки О2. Направление этого движения соответствует  .
. переносим вектор
переносим вектор  в точку C шатуна ВС и смотрим, как она движется относительно точки B. Направление этого движения соответствует. В данном случае угловое ускорение
в точку C шатуна ВС и смотрим, как она движется относительно точки B. Направление этого движения соответствует. В данном случае угловое ускорение