
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулировка и решение 2 задачи динамики .Начальное условие движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вторая или обратная задача: Известна масса точки и действующая на точку сила, необходимо определить закон движение этой точки. Рассмотрим решение этой задачи в декартовой системе координат. Сила зависит от времени, координат точки, ее скорости и других причин.
Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных: Каждая из координат
К этим уравнениям необходимо добавить начальные условия:
Используя эти начальные условия можно получить шесть алгебраических уравнений для определения шести произвольных постоянных
Вопрос Прямолинейное движение материальной точки.прямолинейное движение точки по действием силы зависящей от t x v Дифференциальное уравнение прямолинейного движения точки вдоль оси Оx имеет вид:
Наиболее важные случаи. 1. Сила постоянна. Имеем равнопеременное движение (движение с постоянным ускорением) 2. Сила зависит от времени.
3. Сила зависит от координаты или скорости. Силу, зависящую от координаты х Сила, зависящая от скорости движения В этих случаях решение задачи упрощается.
Вопрос движение точки брошенной под углом к горизонту(траектория,дальность,высота полета) Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
где Координаты тела, следовательно, изменяются так:
При нашем выборе начала координат начальные координаты
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл. Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение (2) в первую формулу (1), получаем:
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов. Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
и подставить его во второе уравнение. Тогда получим:
Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.194.138 (0.006 с.) |

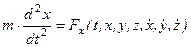 ,
,  ,
,

 движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е.
движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е.


 ,
, 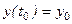

 ,
, 

 , Начальные условия
, Начальные условия 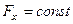

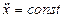




 , создают упругие тела при их деформации (например, сжатая или растянутая пружина).
, создают упругие тела при их деформации (например, сжатая или растянутая пружина).  , это сила сопротивления (воздуха, воды и т.д.)
, это сила сопротивления (воздуха, воды и т.д.) ; проекции ускорения на координатные оси равны ах = 0, ау = -g.
; проекции ускорения на координатные оси равны ах = 0, ау = -g.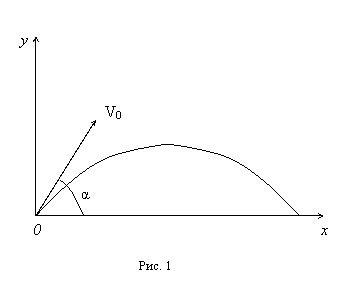 Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1). ,
, – начальная скорость, α – угол бросания.
– начальная скорость, α – угол бросания.
 (рис. 1) Тогда
(рис. 1) Тогда
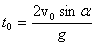 .
.
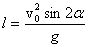 .
.
 .
.

 .
.


