
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена и консолидация платежейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В качестве метода, позволяющего осуществить принцип финансовой эквивалентности обязательств, принято использовать метод приведения (с помощью операций дисконтирования и наращения) платежей к одному моменту времени. При применении метода приведения следует, прежде всего, выбрать базовый момент времени, т.е. момент к которому предполагается приведение всех сумм в расчете. Дисконтирование применяется, если необходимо привести платежи к более ранней дате, наращение – когда базовый момент времени относится к будущему. Пример. Выясните, являются ли равноценными два обязательства, если по одному из них должно быть выплачено 2 млн. рублей через 2 года, а по второму – 2,5 млн. рублей через 3 года. Для сравнения применить сложную процентную ставку 15% годовых. Решение: Найдем современную стоимость этих платежей:
Как видим, данные обязательства не являются равноценными. На практике при изменении условий платежей принцип финансовой эквивалентности реализуется путем составления уравнения эквивалентности, согласно которому сумма заменяемых платежей, приведенных к одному моменту времени, приравнивается к сумме платежей по новому соглашению, приведенных к тому же моменту времени. Для краткосрочных контрактов процесс приведения, как правило, реализуется на основе простых процентных ставок, для среднесрочных и долгосрочных – на основе сложных. Пример. Имеются два кредитных обязательства 400 тыс. руб. и 700 тыс. руб. со сроками уплаты 1 августа и 1 января (следующего года). По согласованию сторон условия обязательств пересмотрены: первый платеж в размере 600 тыс. рублей должник вносит 1 ноября, остальной долг он выплачивает 1 марта. Определите величину второго платежа, если в расчетах используется простая процентная ставка 20% годовых. Проценты точные. Решение: За базовую дату примем дату искомого платежа. Все остальные платежи приведем к этой дате - 1 марта. Срок от 1 августа (Р1=400 тыс. рублей) до 1 марта составляет 212 дней (365-213 +60). Срок от 1 января (Р2=700 тыс. рублей) до 1 марта составляет 59 дней (60-1). Срок от 1 ноября (Р3=600 тыс. рублей) до 1 марта составляет 120 дней (365-305+60). Уравнение эквивалентности имеет вид:
Отсюда Р4=529,65 тыс. рублей.
Пример. Согласно контракту предприятие должно выплатить 200, 300 и 500 тыс. рублей соответственно через 1,5 года, 2 и 4 года. Предприятие предлагает пересмотреть контракт и вернуть долг одним платежом через 3,5 года. Найдите величину консолидированного платежа, если применяется сложная процентная ставка 18% годовых. Решение:
Раздел 5. ОЦЕНКА ЭФФЕКТИВНОСТИ ФИНАНСОВЫХ ОПЕРАЦИЙ 5.1. Доходность финансовых операций.
Одной из важнейших проблем финансового менеджмента является оценка эффективности финансовых операций с целью определения наилучшего варианта инвестирования денежных средств. Результат финансовой операции может оцениваться с помощью показателей дохода или прибыли. Однако один и тот же финансовый доход в разных случаях может быть получен на основе инвестирования значительно отличающихся по объему денежных средств. Поэтому в качестве показателя эффективности финансовой операции, как правило, выбирают показатель доходности, рассчитанный на основе сопоставления дохода, полученного за определенный промежуток времени, с произведенными затратами. Предположим некоторая сумма В качестве показателя доходности может служить: а) обычная годовая ставка процентов, рассчитанная по формуле б) сложная годовая ставка процентов, определенная из формулы наращения по сложным процентам
в) эффективная ставка процентов, если известна номинальная ставка процентов i, и проценты начисляются m раз в год:
(5.3)
Пример Ссуда в размере 2,5 млн. рублей выдана под простые проценты на 2 года, с условием возвратить в конце срока 3,5 млн. руб. Определить доходность этой операции на основе простой и сложной процентных ставок. Решение:
Пример На вклад, помещенный в банк под 16% годовых, проценты начисляются ежеквартально. Оцените доходность этой операции на основе эффективной процентной ставки. Решение: i=0,16; m=4.
В некоторых финансовых операциях общий доход может исчисляться как результат сложения доходов от разных источников. Так, банки кроме взимания процентной ставки за кредит часто устанавливают комиссионное вознаграждение за осуществление операций по расчетным счетам клиентов а также удерживают с клиента определенную сумму, покрывающую затраты банка по каждой операции. Следовательно, измерение доходности любой финансовой операции сводится к учету всех источников дохода, нахождению суммарного дохода за определенный период времени и сопоставлению его с затратами. Для кредитных операций – это сумма денег, предоставленная в кредит. Для владельца ценных бумаг – это сумма, затраченная для их приобретения. При этом все выплаты должны быть приведены к одному моменту времени, чаще всего к сроку начала или окончания финансовой операции. Таким образом, в общем случае оценка доходности сводится к определению расчетной процентной ставки, отражающей общую доходность на вложенный капитал. Пример Ссуда 100 тыс. рублей выдана на 240 дней под 12% годовых. Проценты простые обыкновенные. При выдаче ссуды удержаны комиссионные в размере 1тыс. рублей. Определить полную доходность финансовой операции в виде сложной процентной ставки. Решение: PV=100 тыс. руб.; t = 240 дней; Y = 360 дней. Сумма долга с процентами составит:
Затраты составили 99 тыс. руб. (100-1). Срок финансовой операции Определим полную доходность финансовой операции в виде сложной процентной ставки из равенства: Следовательно, полная доходность этой финансовой операции составляет 13,94%.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 997; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.46.68 (0.007 с.) |







 предоставлена в долг с условием, что через
предоставлена в долг с условием, что через  лет будет возвращена большая сумма
лет будет возвращена большая сумма  .
.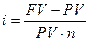 , (5.1)
, (5.1) :
: (5.2)
(5.2)

 или 20%.
или 20%. или 18,3%.
или 18,3%.


 .
.


