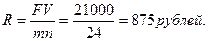Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потребительский кредит. Погашение основного долгаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Равными выплатами Потребительный кредит предоставляется для покупки предметов личного потребления. Существуют различные формы потребительского кредита, отличающиеся друг от друга методами и сроками его погашения. Так, например, кредит может быть предоставлен с отсрочкой платежа и последующим разовым погашением всей суммы. Другой метод предусматривает погашение платежа в рассрочку, частями. Если кредит, выданный потребителю, будет погашен равными выплатами, то наращенная сумма долга будет определяться по формуле: Пример. Холодильник ценой 8 тыс. руб. продается в кредит на два года под 10 % годовых. Погасительные платежи вносятся ежемесячно. Определить размер разового платежа.
Решение: Сумма, подлежащая погашению за весь срок кредита:
Разовый платеж: Погашение потребительского кредита изменяющимися суммами - правило «78». При погашении кредита иногда возникает необходимость определить сумму, идущую на погашение основного долга, и суммы процентных платежей. Такая ситуация возможна, например, при досрочном погашении долга. Для решения этого вопроса можно воспользоваться правилом «78». Для того чтобы объяснить происхождение названия этого правила, рассмотрим следующий пример: Кредит предоставлен на 1 год с ежемесячным погашением. Сумма порядковых номеров месяцев года равна: 1+2+3+4+5+6+7+8+9+10+11+12=78. В соответствии с этим правилом уплата при первом платеже составит величину 12/78 общей начисляемой суммы процентов. А оставшуюся часть платежа пойдет на уплату основного долга. При втором платеже: на оплату процентов идет 11/78 общей суммы начисления процентов, а оставшаяся часть погашает основной долг и т.д. В общем случае знаменатель этих дробей можно определить по формуле: После определения знаменателя, составляют следующую последовательность дробей: Схема с убывающей величиной процентной платы соответствует логике ссудно-заемных операций. Поскольку с течением времени сумма основного долга снижается, то и сумма процентов, начисляемых на непогашенный остаток долга, должна снижаться. Эта схема страхует кредитора на случай досрочного погашения долга, если эта возможность предусмотрена кредитным договором. При досрочном погашении долга заемщик понесет определенный убыток, т.к. большая часть процентов он уже заплатил в начале срока кредитования.
Пример. Кредит в сумме 15000 рублей выдан на 2 года под 20% годовых. Проценты простые. Погашение задолженности производится ежемесячными платежами. Составить план погашения задолженности. Решение: Наращенная сумма долга в конце периода составит Сумма начисленных процентов D = 21 000 – 15 000 = 6 000 рублей. Количество платежей в году - 12, следовательно, за весь рассматриваемый период количество платежей к = 12·2 = 24. Определим значение знаменателя Определим величину разового платежа: В соответствии с правилом «78» уплата при первом платеже составит величину 24/300 общей начисляемой суммы процентов (6 000 рублей). Оставшаяся часть платежа пойдет на уплату основного долга. При втором платеже на оплату процентов пойдет 23/300 общей суммы начисленных процентов, а оставшаяся часть будет направлена на погашен6ие основного долга и т.д. В соответствие с этим получим следующий план погашения долга: (руб.)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1067; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.008 с.) |

 . Сумму разового погасительного платежа, если платеж осуществляется m раз в году, можно определить по формуле:
. Сумму разового погасительного платежа, если платеж осуществляется m раз в году, можно определить по формуле:  .
.


 , где к – количество платежей в году.
, где к – количество платежей в году.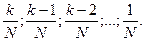 Величина каждой из этих дробей, в сумме составляющих единицу, показывает какая часть общей начисляемой суммы процентов идет на уплату процентов. Оставшаяся часть платежа идет на погашение основного долга.
Величина каждой из этих дробей, в сумме составляющих единицу, показывает какая часть общей начисляемой суммы процентов идет на уплату процентов. Оставшаяся часть платежа идет на погашение основного долга.