
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая конечная рента. Эквивалентность рентСодержание книги Поиск на нашем сайте
Если платежи осуществляются p раз в год, а начисление процентов m раз в год, то конечная стоимость ренты равна
Sn =
Начальная стоимость ренты в этом случае будет равна
S0=
Пример 18. Создается фонд в течение n = 5 лет. Взносы составляют R = 120 тыс. руб. в год при номинальной ставке j= 12% годовых. Определить размер фонда при различных параметрах платежей p и начислений процентов m.
Решение удобно выполнить в таблице.
Как это видно из примера условия производства платежей и начисления процентов (их частота) заметно влияют на размер наращенной суммы. Ниже приведены соотношения наращенных сумм соответствующих финансовых рент.
Sn(1;1)< Sn(1;m)< Sn(1;∞)< Sn(p;1)< Sn(p;m)< Sn(p;∞).
Для начальной стоимости ренты эти соотношения будут
S0(1;∞)< S0(1;m)< S0(1;1)< S0(p;∞)< S0(p;m)< S0(p;1). Задачи для самостоятельного решения Задача 20. Найти современную стоимость ренты R = 120тыс. руб. в год. Платежи осуществляются в течение n = 5 лет при номинальной ставке j = 12% годовых.
Решение задачи выполните в предлагаемой таблице
Задача 21. Некто хочет накопить 160 тыс. руб. за 5 лет при 30% годовых. Какую сумму необходимо вкладывать ежемесячно и ежедневно? Решение.
Задача 22. Некто хочет приобрести в кредит на 5 лет автомобиль при 30% годовых за 160 тыс. руб. Сколько придется платить ежемесячно? Решение.
Задача 23. Некто хочет накопить 160 тыс. руб. для покупки автомобиля при 30% годовых, имея возможность откладывать 500 руб. в месяц. Сколько лет придется копить?
Решение.
Задача 24. Под какой процент надо вкладывать по 500 руб. в месяц, чтобы накопить за 5 лет 160 тыс. руб.? Решение.
Задача 25. Семья хочет накопить 12000 долл., вкладывая в банк по 100 долл. ежемесячно. Годовая номинальная ставка равна 7% при ежеквартальном начислении процентов. Как долго придется копить? Решение. Эквивалентные ренты
Объединение и замена рент выполняется по следующему общему правилу: находятся современные величины рент-слагаемых и складываются, а затем подбирается рента-сумма с такой же современной величиной и нужными остальными параметрами.
Пример 19. Найти ренту-сумму для двух годовых рент: одна длительностью 5 лет с годовым платежом 1000, и другая − 8 и 800. Годовая ставка процента 8%.
Решение. По таблицам или вычисляя по формуле (4) находим
S1 = 1000 F4 (0.08, 5) = 1000∙3,993 =1000 [1− (1+0.08) –5 ]/0.08) = 3993.
S2 = 800 F4 (0.08, 8) = 800∙5,747 = 800 [1-(1+0.08)– 8/0.08) = 4597.
S∑ = 3993+4597 = 8590.
Теперь можно задать либо длительность ренты-суммы, либо годовой платеж и затем второй из этих параметров определится.
При R = 1000ед./год n = [ln((1− (S0/R)i)) –1]/ ln(1+i) = [ln((1−(8590/1000)0,08)) –1]/ ln(1+0,08) = 15,1 лет.
Для n = 10 лет рентный платёж будет равен R = S0 i / [1− (1+i)–n] = 8590∙0,08 / [1− (1+0,08)–10] = 1280 ед. в год.
Задача 26. Покупатель предложил два варианта расчетов для продавца дачи. 1) 5000 долл. сейчас и по 1000 долл. в год в течение 5 лет. 2) 8000 долл. немедленно и по 300 долл. в год в течение 5 лет. Какой вариант выгоднее продавцу? Решение.
Основные выводы по теме 1.Если платежи осуществляются p раз в год, а начисление процентов m раз в год, то конечная и начальная стоимость ренты определяются по более сложным формулам (10), (11).
2. Условия производства платежей p и начисления процентов m (их частота) заметно влияют на размер наращенной суммы.
3. Объединение и замена рент выполняется по следующему общему правилу: находятся современные величины рент-слагаемых и складываются, а затем подбирается рента-сумма с такой же современной величиной и нужными остальными параметрами.
1.5. Контрольные вопросы по разделу 1
1. Почему берутся проценты при даче ссуды? 2. Каковы причины различной стоимости денег в разные моменты времени? 3. Почему вопросы временной стоимости денег стали более актуальными в последнее время? 4. Как называется процесс приведения денег из настоящего в будущее время? 5. Как называется процесс приведения денег из прошлого в настоящее время? 6. Как называется процесс приведения денег из будущего в настоящее время? 7. Как называется процесс приведения денег из настоящего в прошлое время? 8. Что такое математическое дисконтирование? 9. Назовите основные параметры приведения денег по фактору времени? 10. Почему вопросы дисконтирования (приведения) денежных потоков актуальны в инвестиционном анализе? 11. Почему в инвестиционном анализе используются сложные проценты? В чем отличие сложных и простых процентов? 12. В чем различие процентных и учетных ставок? 13. Что такое эффективная процентная ставка? 14. Как влияют параметры приведения i и n на наращенную сумму? 15. Как влияют параметры приведения i и n на дисконтированную сумму? 16. Как влияет периодичность начисления процентов на наращенную сумму? 17. Как влияет периодичность начисления процентов m на дисконтированную сумму?
18. Что такое потоки платежей и почему их необходимо изучать? 19. Как определить величину (стоимость) потока денежных платежей? 20. Назовите основные разновидности потоков платежей? 21. Что означают ординарные и неординарные потоки денежных платежей? 22. Что означают регулярные и нерегулярные потоки денежных платежей? 23. Что такое финансовая рента? В чем ее отличие от произвольного потока денежных платежей? 24. Перечислите основные параметры финансовой ренты? 25. Какие существуют дополнительные параметры у общей конечной ренты? 26. Как влияют авансовые платежи (пренумерандо) на текущую стоимость потока денежных платежей? 27. Как влияют авансовые платежи (пренумерандо) на будущую стоимость потока денежных платежей? 28. Чем отличается постоянная конечная рента от общего случая финансовой ренты? 29. Как определить начальную стоимость постоянной конечной ренты? 30. Как определить конечную стоимость постоянной ренты? 31. Что такое коэффициент наращения ренты F3(i, n)? 32. Что такое коэффициент приведения ренты F4(i, n)? 33. Как влияет перенос рентных платежей R в начало периода t на современную стоимость финансовой ренты? 34. Как влияет перенос рентных платежей R в начало периода t на конечную стоимость финансовой ренты? 35. Приведите практические примеры определения современной стоимости ренты? 36. Приведите практические примеры определения конечной стоимости ренты? 37. Что такое коэффициент ренты F5(i, n)? 38. Что такое коэффициент ренты F6(i, n)? 39. Что такое вечная рента и как определить её стоимость? 40. Из какого условия можно найти процентную ставку i при известном рентном платеже и сроке ренты?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.64.124 (0.012 с.) |

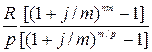 .
.  (10)
(10) .
. 


