
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы финансовой математикиСодержание книги Поиск на нашем сайте ИНВЕСТИЦИИ И ИНВЕСТИЦИОННЫЙ АНАЛИЗ Рабочая тетрадь
Челябинск Издательский центр ЮУрГУ ББК У9(2)–56.я7 Г604
Одобрено учебно-методической комиссией филиала в г. Озёрске
Рецензент А.Г.Бутрин
© Издательский центр ЮУрГУ, 2013 ВВЕДЕНИЕ Рабочая тетрадь предназначена для упражнений на практических занятиях при изучении курса «Инвестиции и инвестиционный анализ» и может использоваться студентами заочной формы обучения при самостоятельном изучении предмета, поскольку по каждой изучаемой теме приведены краткие теоретические положения, примеры решаемых задач, основные выводы и вопросы для самоконтроля. Целью данной работы является освоение студентами экономических специальностей основ общепринятых в мировой практике подходов к оценке эффективности и финансовой реализуемости инвестиционных проектов на простейших примерах, рассматриваемых в данном учебном пособии. При подготовке пособия были использованы материалы из книг [2, 3, 4, 5]. Инвестиционная деятельность имеет исключительно большое значение, поскольку создает основы для стабильного развития экономики в целом, отдельных ее отраслей и конкретных хозяйствующих субъектов. Особую актуальность приобретает реальное промышленное инвестирование различных проектов и мероприятий, направленных на создание, обновление и расширенное воспроизводство основных производственных фондов и связанное с ним производство конкурентоспособной продукции. Сущность инвестиций в условиях рыночной экономики заключается в сочетании двух сторон инвестиционной деятельности: затрат ресурса и получение результата. Правильность оценки полученных результатов в равной степени зависит от полноты и корректности методов, используемых при инвестиционном анализе, от опыта и квалификации специалистов и консультантов. В связи с этим особое значение приобретает изучение методов оценки и обоснования инвестиционных проектов. Комплексная оценка инвестиционного проекта производится в соответствии с «Руководством по оценке эффективности инвестиций» [1] разработанным Международным центром промышленных исследований при ЮНИДО и опубликованным в 1978 году. На основе этого подхода в России в 1994 году были подготовлены и изданы «Методические рекомендации по оценке эффективности инвестиционных проектов и их отбору для финансирования» [6], которые в 2000 году (вторая редакция) были уточнены и дополнены [7],что свидетельствует об актуальности инвестиционной деятельности для России.
ОСНОВЫ ФИНАНСОВОЙ МАТЕМАТИКИ
Временная стоимость денег
Денежные суммы изменяются во времени. Люди берут ссуды и самим ссужают деньги. При этом они намерены приобрести бизнес и за счет будущих доходов выплатить займ или накопить на машину или путешествие и для этого откладывают деньги на сберегательный счет. Для того, чтобы заинтересовать других людей давать ссуду, им обязуются вернуть в будущем бо'льшую сумму (то есть с процентом). Это и есть основание теории процентов. Под процентными деньгами или кратко процентами (interest), в финансовых расчетах понимают абсолютную величину дохода от предоставления денег в долг в любой его форме: выдача денежной ссуды, продажа в кредит, помещение денег на сберегательный счет, учет векселя, покупка сберегательного сертификата или облигации и т. д. Какой бы вид не имели проценты, это всегда конкретное проявление такой экономической категории, как ссудный процент. Практика выплаты процентов за выданные в долг деньги существовала задолго до нашей эры. Например, в Древней Греции взымали от 10 до 36% в год. По «Русской Правде» годовой рост занятого капитала определялся в 40%. В современных условиях проценты − один из важнейших элементов любых видов инвестиционных, кредитных и коммерческих контрактов, экономических договоров и соглашений. При заключении финансового соглашения стороны (кредитор и заёмщик) договариваются о размере процентной ставки (rate of interest) − отношения суммы процентных денег, выплачиваемых за фиксированный отрезок времени к величине ссуды. Интервал времени, к которому приурочена процентная ставка, называют периодом начисления. Сумму процентных платежей определяют исходя из размера ссуды, общего её срока и уровня процентной ставки. Ставка измеряется в процентах или долях, в виде натуральной или десятичной дроби (размерностью − 1/период). Таким образом: 1) Деньги являются специфическим экономическим ресурсом и, как и любой другой ресурс имеют свою цену. 2) Ресурс для своего использования требует времени. Существуют различные ставки и способы начисления процентов, зависящие от условий контрактов, формы осуществления операций или сделок. Начисление процентов, как правило, происходит дискретно, причем в качестве периодов начисления принимают год, полугодие, квартал, месяц. Иногда практикуют ежедневное начисление, а в ряде случаев (например, в анализе долгосрочных операций) удобно применять непрерывные проценты. Существуют процентные и учетные ставки. Различие между ними обусловлено выбором исходной базы (суммы) для начисления процентов.
Если текущую сумму обозначить ─ S0, а возвращаемую (наращенную) сумму ─ Sn, то для процентной ставки i сумма процентов Sn─ S0, начисленная за один период, относится к текущей стоимости i = (Sn─ S0)/ S0, а для учетной ставки d к будущей наращенной стоимости d = (Sn─ S0)/ Sn. Проценты по ставке i в профессиональной банковской литературе называют декурсивными, а по ставке d антисипативными. Связь между этими ставками можно выразить формулами:
i = d / (1─d) и d = i / (1+ i). (1)
Отсюда можно увидеть, что процентная ставка всегда больше учетной i > d (или равна ей, учитывая случай непрерывного начисления процентов, когда разность Sn– S0 стремится к нулю). Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего периода начисления (простые процентные ставки) или к сумме с начисленными в предыдущем периоде процентами (сложные процентные ставки). При начислении простых процентов суммы изменяются в арифметической прогрессии (возрастающей или убывающей), так как каждый последующий член увеличивается или уменьшается на постоянную величину. При начислении сложных процентов суммы изменяются в геометрической прогрессии (возрастающей или убывающей), так как каждый последующий член умножается или делится на постоянную величину. В инвестиционном анализе, как правило, используется процентная ставка, а не учетная и сложные проценты, а не простые. Специфика реальных промышленных инвестиций заключается в том, что вкладываются большие суммы, на продолжительный срок, а получаемые в будущем доходы очень часто реинвестируются. Отсюда следует необходимость учета фактора времени в инвестиционных расчетах. Фактор времени, особенно в долгосрочных операциях, играет не меньшую роль, чем размеры денежных сумм. Финансовые операции, проводимые в инвестиционной деятельности, заключаются во вложении капитала сейчас на определенный период, а затем получении в будущем увеличенного капитала. Необходимость учета фактора времени определяется сущностью самого процесса финансирования и кредитования и выражается в виде принципа неравноценности денег, относящихся к разным моментам времени (time-value of money). Будущие деньги дешевле сегодняшних денег. В самом деле, даже если отвлечься от обесценивающей их инфляции и риска инвестирования, отмеченная неравноценность двух одинаковых сумм определяется, прежде всего, тем, что теоретически любая сумма может быть инвестирована и принести доход. Очевидным следствием принципа неравноценности денег является неправомерность суммирования денежных величин, относящихся к разным моментам времени в финансовом и экономическом анализе.
Таким образом, основными причинами, определяющими различную стоимость денег в разные моменты времени являются: 1) альтернативность инвестирования, обусловленная свободой выбора; 2) инфляция; 3) риск.
Денежные суммы S(T) в момент времени Т и s(t) в момент t называются эквивалентными по ставке сравнения i, если S(T) = s(t)(1+ i)(Т– t). При T>t это означает, что сумма s(t), наращенная по ставке i cложных процентов, превратится в момент Т в сумму S(T); однако можно считать, что Т может быть и меньше t, тогда это означает, что сумма S(T), наращенная по ставке i сложных процентов, превратится, в момент t в сумму s(t). Указанная выше формула автоматически учитывает оба эти случая. Вместе с тем можно сказать и по другому: при Т>t эквивалентность сумм S(T) и s(t) означает, что сумма S(T), уменьшающаяся при движении в прошлое за каждый единичный промежуток в 1/(1+i) раз, к моменту t превратится в точности в сумму s(t) = S(T)/[(1+ i)(Т– t)]. Такой пересчет будущей суммы к настоящему моменту называется приведением или нахождением её современной величины. Сама же формула сравнения денежных сумм в любые моменты времени называется математическим дисконтированием. Выбирая точку приведения на оси времени Т=0 и учитывая знак t, получим:
S0 = St αt = St (1+ i) –t, (2)
где αt ─ общая функция (коэффициент) приведения по фактору времени; St ─ номинальная сумма в момент времени t; S0 ─ приведенная сумма в момент времени t = 0; i ─ процентная ставка в долях на период; t ─ номер периода (шаг расчета). Очевидно, что при t > 0 коэффициент приведения αt >1, то есть при движении из прошлого в настоящее и из настоящего в будущее происходит наращение (капитализация, компаундирование, мультиплицирование). При t < 0 коэффициент приведения αt < 1, то есть при движении из будущего в настоящее и из настоящего в прошлое происходит дисконтирование (discount ─ скидка, снижение). Логика таких процессов представлена на рис.1.

Рис. 1. Эквивалентность денежных сумм в разные моменты времени
Величина (1+i)t = F1(i, t) называется мультиплицирующим множителем (коэффициентом). Величина (1+i)–t = F2(i, t) называется дисконтным множителем (коэффициентом). Эти коэффициенты являются распространенными и поэтому табулированы (см. приложение). Итак, в любой финансовой сделке (см. формулу 2) присутствуют четыре величины исходная сумма St, приведенная сумма S0, процентная ставка i и временной период t. Отсюда возникает четыре типа задач: вычисление наращенной суммы инвестиций; вычисление текущей стоимости инвестиций; вычисление периода (срока) финансовой операции; вычисление процентной ставки.
Пример 1. Вкладчик положил в банк сумму S0 = 3000 руб. под 30% годовых на срок t = 5 лет. Определить величину возвращаемой суммы.
Решение. St = S0 αt = S0 (1+i)t = 3000(1+0,3)5= 3000∙3,713=11139 руб.
Пример 2. Вкладчик хочет накопить за t = 5лет сумму St = 56000 руб., при годовой ставке 30%. Сколько требуется положить на срочный вклад «сегодня» для получения желаемой суммы.
Решение. S0 = St αt = St (1+i)–t = 56000(1+0,3) –5= 56000∙0,269=15082 руб.
Пример 3. Вкладчик положил в банк сумму S0 = 2000 $ под 14% годовых. Через сколько лет накопится St = 10 000 $?
Решение. Срок наращения определится из условия: St = 2000(1+0,14) t =10000.
Тогда t =
Пример 4. Вкладчик имеет S0 = 5000 руб. Под какой процент необходимо положить эту сумму, чтобы получить через t = 3года St = 10000 руб.?
Решение. Процентная ставка определится из условия: St = 5000(1+ i)3 =10000.
Тогда i =
Таким образом, рассмотрев формально формулу (2) состоящую из четырёх параметров видно, что вычисление каждого из них через известные другие имеет реальный практический смысл. Вычисления по сложной процентной ставке, то есть когда возникает ситуация начисления процента на процент можно проиллюстрировать на следующем примере. Пример 5. Предприятию в начале года выдан кредит в размере 400 тыс. руб. на полгода (6 месяцев) под 5 % в месяц. а) Какова будет величина долга в конце каждого месяца?
Решение. Применим многократно формулу (2).
В конце 1-го месяца долг составит 400,0∙1,05 = 420,0 тыс. руб. В конце 2-го месяца долг составит 420,0∙1,05 = 441,0 тыс. руб. В конце 3-го месяца долг составит 441,0∙1,05 = 463,0 тыс. руб. В конце 4-го месяца долг составит 463,0∙1,05 = 486,0 тыс. руб. В конце 5-го месяца долг составит 486,0∙1,05 = 510,5 тыс. руб. В конце 6-го месяца долг составит 510,5∙1,05 = 536,0 тыс. руб.
То есть предприятию через полгода необходимо вернуть 536 тыс. руб. в том числе основной долг 400 тыс. руб. и проценты 136 тыс. руб. (536=400+136). Итоговую сумму возврата долга можно вычислить быстрее, используя ту же формулу и учитывая число периодов начисления процентов. В конце 6-го месяца долг составит St = 400(1+0,05)6 = 400∙1,056 = 536 тыс. руб.
б) Какова будет величина долга в конце года при тех же условиях кредита?
Решение. В этом случае будет 12 периодов (месяцев) начисления процентов. St = 400(1+0,05)12 = 400∙1,0512 = 400∙1,796 = 718,3 тыс. руб.
в) Какой же годовой процент (то есть за один период начисления) соответствует (эквивалентен) выше рассмотренным условиям кредита? Решение. St = 400∙1,796 = 400(1+0,796)1 = 400∙(1+iэ)1 = 718,3 тыс. руб. Отсюда видно, что iэ = 0,796 или 79,6 % в год, хотя номинальная ставка равна j = 5 % мес. ∙12мес./год = 60 % в год. Обычно в договорах принято указывать номинальную годовую ставку j и другие дополнительные условия кредита, например параметр m − число раз в году начисления процентов. В этом случае эффективная годовая ставка процента iэ показывает, какую годовую ставку следует установить при однократном начислении процентов, чтобы получить тот же финансовый результат − капитализацию инвестиций, что и при m кратном начислении процентов по ставке j/m. Формула расчета эффективной ставки имеет вид: iэ = (1 + j/m)m –1, (3)
Пример 6. Депозит в размере S0 = 5000 руб. внесен в банк под j =36 % годовых. а) Определить наращенную сумму через 4 года?
Решение. St = 5000∙(1+0,36)4 = 5000∙3,421 = 17105 руб.
б) Определить тоже самое при полугодовом начислении процентов (m = 2)?
Решение. St = 5000∙(1+0,36/2)2∙4 = 5000(1+0,18)8 = 5000∙3,759 = 18794 руб.
в) Определить тоже самое при поквартальном начислении процентов (m = 4)?
Решение. St = 5000∙(1+0,36/4)4∙4 = 5000(1+0,09)16 = 5000∙3,970 = 19852 руб.
г) Определить тоже самое при ежемесячном начислении процентов (m = 12)?
Решение. St = 5000∙(1+0,36/12)12∙4 = 5000(1+0,03)48 = 5000∙4,132 = 20661 руб.
д) Определить тоже самое при ежедневном начислении процентов (m = 360)?
Решение. St = 5000∙(1+0,36/360)360∙4 = 5000(1+0,001)1440= 5000∙4,218 = 21088 руб.
е) Определить тоже самое при непрерывном начислении процентов (m → ∞)?
Решение. При m → ∞ lim (1+j/m)m = ej, тогда
St = 5000∙e 0,36∙4 = 5000∙ e 1,44 = 5000∙4,221 = 21103 руб.
Из результатов примера 6 видно, что периодичность начисления процентов m существенно влияет на наращенную сумму (увеличивает её), то есть эффективная процентная ставка iэ тем больше, чем больше m и номинальная ставка j. Непрерывное начисление процентов при заданных исходных данных оказалось близким по результатам наращения к ежедневному начислению. Необходимо отметить, что формула (2) имеет место только в случае неизменной во времени сложной процентной ставке. При переменной по годам (периодам начисления) процентной ставке возникает произведение коэффициентов наращения. Пример 7. По договору займа предусмотрена следующая схема начисления сложных процентов: за первый год − 60 % годовых, за каждое последующее полугодие ставка повышается на 10 % (процентных пунктов). Определить коэффициент наращения за 2,5 года? Решение. αt=1∙(1+0,6)(1+
Задачи для самостоятельного решения. Задача 1. Вкладчик хочет получить через 5 лет 5000 руб. при номинальной годовой ставке 10 %. а) Определить какую сумму необходимо положить на депозит? Решение.
б) Определить то же, что и при предыдущих условиях, но при ставке 20 %.? Решение.
в) Определить то же, при предыдущих условиях, но при сроке 10лет? Решение.
г) Определить то же, при предыдущих условиях, но при ежеквартальном начислении процентов? Решение.
д) Определить то же, при предыдущих условиях, но при ежемесячном начислении процентов? Решение.
е) Определить то же, при предыдущих условиях, но при ежедневном начислении процентов? Решение.
ж) Определить то же, при предыдущих условиях, но при непрерывном начислении процентов? Решение. Задача 2. В 1624 году остров Манхеттен в центре Нью-Йорка был «куплен» у индейского вождя за 24 долл. Спустя 350 лет (в 1974 году) стоимость земли оценивалась примерно в 40 млрд. долл. Определите, какой средней ставке процентов годовых соответствует такой рост суммы? Решение.
Задача 3. На вашем счете в банке 4000 руб. при 18 % годовых. Вам предлагают войти в венчурный проект и обещают через 6 лет утроение капитала. Что ответить: а) если не учитывать риск «венчура» и б) если учесть риск венчурного проекта в 5 % годовых? Решение.
Задача 4. Рассчитать таблицу эффективных ставок при различной частоте начисления процентов m и заданной номинальной ставке j. Решение.
Задача 5. Некто хочет накопить на автомобиль ценой в 300 тыс. руб. за 5 лет. а) Сколько необходимо внести в банк сейчас на срочный вклад при процентной ставке 20 % годовых? Решение.
б) Через сколько лет возможно осуществление данной цели при возможности вклада 15 тыс. руб. при той же ставке процентов? Решение.
в) Под какой процент необходимо внести средства для осуществления данной цели, если возможность вклада составляет 15 тыс. руб.? Решение.
г) Какой цены автомобиль можно купить через 5 лет при тех же возможностях инвестора и тех же условиях банка? Решение.
Основные выводы по теме Из рассмотренных примеров и задач следует: 1.Сложные проценты изменяют первоначальную сумму в геометрической прогрессии. 2. Параметрами приведения по фактору времени являются: ─ исходная (текущая) сумма S0; ─ приведенная сумма St; ─ процентная ставка i; ─ количество периодов начисления процентов t. 3. Ставка процентов может меняться во времени, тогда в общем коэффициенте приведения вместо степени получаем произведение индексов приведения. 4. Период начисления процентов m увеличивает влияние процентов (эффективная ставка процентов больше номинальной ставки при m > 1). 5. Сила роста сложных процентов значительна при больших отрезках времени. 6. Повышенный риск инвестора требует большей доходности инвестиций.
Основные выводы по теме
1. Для нахождения стоимости потока платежей необходимо привести каждый платеж к одному моменту времени и затем их алгебраически сложить (не правильно складывать неприведенные платежи). 2. Наращенная и современная стоимость денежного потока находятся в такой же временной связи, как и разовые отдельные платежи (отличаются в (1+i)T раз). 3. Авансовые платежи (платежи пренумерандо) увеличивают и современную и конечную стоимость потока в (1+i) раз. 4. Стоимость постоянной ренты равна сумме членов геометрической прогрессии. Для конечной стоимости ренты − возрастающая прогрессия. Для начальной стоимости ренты − убывающая прогрессия. 5. Коэффициент наращения постоянной конечной ренты показывает во сколько раз конечная (наращенная) стоимость ренты больше её рентного платежа и является будущей стоимостью единичного денежного потока, длящегося n периодов с процентной ставкой i. 6. Коэффициент приведения постоянной конечной ренты показывает во сколько раз начальная (дисконтированная) стоимость ренты больше её рентного платежа и является современной стоимостью единичного денежного потока, длящегося n периодов с процентной ставкой i. 7. Перенос рентных платежей в начало периода (платежи пренумерандо) увеличивают стоимость ренты в (1+i) раз.
Основные выводы по теме
1.Определение члена ренты R (рентного платежа) при известных i и n, задача обратная определению наращенной или современной стоимости ренты.
2.Табулированный коэффициент F5(i, n) = 1/F3(i, n) = i / [(1+i)n−1] показывает, какую одинаковую величину необходимо периодически вносить n лет под i %, для формирования фонда в одну денежную единицу.
4.Определение срока ренты n по известным R и i можно выполнить по формулам (8), (9) или воспользоваться таблицами F3(i, n), F4(i, n).
5.Процентная ставка i при заданных R и n определяется приближенно итерациями из условия [(1+i) n −1]/ i = S n / R или [1− (1+i)– n]/i = S0 / R.
Эквивалентные ренты
Объединение и замена рент выполняется по следующему общему правилу: находятся современные величины рент-слагаемых и складываются, а затем подбирается рента-сумма с такой же современной величиной и нужными остальными параметрами.
Пример 19. Найти ренту-сумму для двух годовых рент: одна длительностью 5 лет с годовым платежом 1000, и другая − 8 и 800. Годовая ставка процента 8%.
Решение. По таблицам или вычисляя по формуле (4) находим
S1 = 1000 F4 (0.08, 5) = 1000∙3,993 =1000 [1− (1+0.08) –5 ]/0.08) = 3993.
S2 = 800 F4 (0.08, 8) = 800∙5,747 = 800 [1-(1+0.08)– 8/0.08) = 4597.
S∑ = 3993+4597 = 8590.
Теперь можно задать либо длительность ренты-суммы, либо годовой платеж и затем второй из этих параметров определится.
При R = 1000ед./год n = [ln((1− (S0/R)i)) –1]/ ln(1+i) = [ln((1−(8590/1000)0,08)) –1]/ ln(1+0,08) = 15,1 лет.
Для n = 10 лет рентный платёж будет равен R = S0 i / [1− (1+i)–n] = 8590∙0,08 / [1− (1+0,08)–10] = 1280 ед. в год.
Задача 26. Покупатель предложил два варианта расчетов для продавца дачи. 1) 5000 долл. сейчас и по 1000 долл. в год в течение 5 лет. 2) 8000 долл. немедленно и по 300 долл. в год в течение 5 лет. Какой вариант выгоднее продавцу? Решение.
Основные выводы по теме 1.Если платежи осуществляются p раз в год, а начисление процентов m раз в год, то конечная и начальная стоимость ренты определяются по более сложным формулам (10), (11).
2. Условия производства платежей p и начисления процентов m (их частота) заметно влияют на размер наращенной суммы.
3. Объединение и замена рент выполняется по следующему общему правилу: находятся современные величины рент-слагаемых и складываются, а затем подбирается рента-сумма с такой же современной величиной и нужными остальными параметрами.
1.5. Контрольные вопросы по разделу 1 1. Почему берутся проценты при даче ссуды? 2. Каковы причины различной стоимости денег в разные моменты времени? 3. Почему вопросы временной стоимости денег стали более актуальными в последнее время? 4. Как называется процесс приведения денег из настоящего в будущее время? 5. Как называется процесс приведения денег из прошлого в настоящее время? 6. Как называется процесс приведения денег из будущего в настоящее время? 7. Как называется процесс приведения денег из настоящего в прошлое время? 8. Что такое математическое дисконтирование? 9. Назовите основные параметры приведения денег по фактору времени? 10. Почему вопросы дисконтирования (приведения) денежных потоков актуальны в инвестиционном анализе? 11. Почему в инвестиционном анализе используются сложные проценты? В чем отличие сложных и простых процентов? 12. В чем различие процентных и учетных ставок? 13. Что такое эффективная процентная ставка? 14. Как влияют параметры приведения i и n на наращенную сумму? 15. Как влияют параметры приведения i и n на дисконтированную сумму? 16. Как влияет периодичность начисления процентов на наращенную сумму? 17. Как влияет периодичность начисления процентов m на дисконтированную сумму?
18. Что такое потоки платежей и почему их необходимо изучать? 19. Как определить величину (стоимость) потока денежных платежей? 20. Назовите основные разновидности потоков платежей? 21. Что означают ординарные и неординарные потоки денежных платежей? 22. Что означают регулярные и нерегулярные потоки денежных платежей? 23. Что такое финансовая рента? В чем ее отличие от произвольного потока денежных платежей? 24. Перечислите основные параметры финансовой ренты? 25. Какие существуют дополнительные параметры у общей конечной ренты? 26. Как влияют авансовые платежи (пренумерандо) на текущую стоимость потока денежных платежей? 27. Как влияют авансовые платежи (пренумерандо) на будущую стоимость потока денежных платежей? 28. Чем отличается постоянная конечная рента от общего случая финансовой ренты? 29. Как определить начальную стоимость постоянной конечной ренты? 30. Как определить конечную стоимость постоянной ренты? 31. Что такое коэффициент наращения ренты F3(i, n)? 32. Что такое коэффициент приведения ренты F4(i, n)? 33. Как влияет перенос рентных платежей R в начало периода t на современную стоимость финансовой ренты? 34. Как влияет перенос рентных платежей R в начало периода t на конечную стоимость финансовой ренты? 35. Приведите практические примеры определения современной стоимости ренты? 36. Приведите практические примеры определения конечной стоимости ренты? 37. Что такое коэффициент ренты F5(i, n)? 38. Что такое коэффициент ренты F6(i, n)? 39. Что такое вечная рента и как определить её стоимость? 40. Из какого условия можно найти процентную ставку i при известном рентном платеже и сроке ренты? И постоянными доходами Пусть первоначальные единовременные инвестиции составляют К0 а поток будущих доходов постоянен В этом случае расчеты оценки эффективности проекта существенно упрощаются и представляют собой известные формулы современной стоимости постоянной конечной ренты.
Чистый дисконтированный доход равен ЧДД = R [1– (1+i)– n]/i − К0 = R F4 (i, n) − К0 ³ 0. (27)
Индекс доходности будет ИД = (1/К0)R [1– (1+i)– n]/i = (R/ К0) F4 (i, n) = (ЧДД+ К0) / К0 ³ 1. (28)
Срок окупаемости инвестиций Ток = n = [ln((1– (К0 /R)i)) –1]/ ln(1+i). (29)
Внутренняя норма доходности найдется из условия R [1– (1+ ЕВН)– n ]/ ЕВН – К0 = 0 (30)
или подбором по таблице F4 (ЕВН, n) = К0 / R и уточнением интерполяцией
ЕВН ≈ i1 + [F4 (i1, n) – (К0/R)] (i2 – i1 ) / [F4 (i1, n) – (F4 (i2, n)],
где i1< ЕВН, а i2 > ЕВН.
Пример 20. Выполнить расчеты и оценить эффективность проекта по созданию торговой точки (в течение месяца) с начальными инвестициями К0 = 10000 долл., которая будет приносить доход R = 3000 долл. в год в течении n =10 лет. Ставка процента i = 0,08 1/год. Дополнительно оценить максимально допустимые инвестиции, минимально допустимый доход, влияние колебаний ставки процента i1= 0,1 и i2 = 0,3 и целесообразность аренды торговой точки по сравнению со строительством при арендных платежах 2000 и 1000 долл. в год. Решение. ЧДД = 3000 [1– (1+0,08)– 10]/0,08− 10000 = 3000 F4 (0,08, 10) − 10000 = 3000∙6,710 – 10000 = 10130 долл. > 0.
Индекс доходности равен ИД = (3000/ 10000) [1– (1+0,08)– 10]/0,08 = (3000/ 10000)F4 (0,08, 10) = (3/10)∙6,710 = (10130+ 10000)/10000 = 2,013 > 1. Срок окупаемости инвестиций определится по формуле (28) Ток = n = [ln(1– (10000∙0,08/3000)) – 1]/ ln(1+0,08) =ln(1,3636)/ ln(1,08) = 4.03 лет, что меньше 10 лет.
Внутреннюю норму доходности определим, используя таблицу F4 (i, n) = 3,333 (см. приложение). Так F4 (0,25; 10) = 3,570, а F4 (0,30; 10) = 3,092.
Рассчитаем приближенно ЕВН ≈ 0,25+(3,570 – 3,333)(0,30 – 0,25)/(3.570 – 3.092) = 0.275, то есть 27,5% годовых, что больше принятой ставки дисконтирования 8%.
Отсюда следует, что по всем показателям проект является эффективным.
Оценим максимально допустимые инвестиции из условия ЧДД = 0. К0 < R [1– (1+i)– n]/i = R F4 (i, n) = 3000∙6,710 =20130 долл.
Оценим минимально допустимые доходы R из этого же условия. R > К0 i / [1– (1+i)– n] = 10000/6.710 = 1490 долл. в год.
Оценим влияние ставки дисконтирования. При ставке процента i1 = 0,1 чистый дисконтированный доход равен
ЧДД1 = R [1– (1+i)– n]/i − К0 = R F4 (i, n) − К0 = = 3000 [1– (1+0,1)– 10]/0,1− 10000 = 3000 F4 (0,1;10) − 10000 = 3000∙6,145 – 10000 = =18434 − 10000 = 8434 долл. то есть доходность проекта снижается.
При ставке процента i2 = 0,3 ЧДД2 = 3000 [1– (1+0,3)– 10]/0,3− 10000 = 3000F4 (0,3;10) − 10000 = = 3000∙3,0915 – 10000 = − 726 долл. то есть доходность проекта отрицательная.
Целесообразность аренды можно установить, рассчитав современную стоимость арендных платежей за 10 лет при остаточной стоимости равной нулю.
S1= 2000 F4 (0,08, 10) = 2000∙6,710 = 13422 долл. > 10000 долл. аренда не выгодна.
S2= 1000 F4 (0,08, 10) = 1000∙6,710 = 6710 долл. < 10000 долл. аренда выгодна.
Задача 27. Выполнить расчеты и оценить эффективность инвестиций в предприятие в размере К0 = 4000 ден. ед., которое будет приносить ежемесячный доход R = 100 ден. ед. в течении n =6 лет. Инвестор имеет альтернативу вложения средств с доходностью 12% годовых при ежемесячном начислении процентов.
Дополнительно оценить максимально допустимый уровень инвестиций, минимально допустимый ежемесячный доход, влияние колебаний ставки процента i1= 0,10 и i2 = 0,24 и целесообразность аренды предприятия по сравнению со строительством при ежемесячной арендной плате 90 ден. ед. Решение. Основные выводы по теме 1. Для проектов с первоначальными единовременными инвестициями и постоянными доходами, денежные потоки представляют собой обычные постоянные ренты (конечные постоянные аннуитеты). В этом случае расчеты оценки эффективности проекта существенно упрощаются для всех показателей.
2. Используя условие ЧДД = 0 можно найти максимально допустимые инвестиции и минимально допустимые доходы.
3. Увеличение ставки дисконтирования снижает эффективность проекта.
4. Оценку альтернативы аренда − покупка можно выполнить по текущей стоимости арендных платежей.
Основные выводы по теме 1. Для расчета эффективности проектов с переменными доходами необходимо воспользоваться формулами (12),(16),(18) и (20) расчета показателей эффективности в общем виде с пошаговым вычислением денежных потоков. Такие расчеты удобно выполнять в таблице.
2. Приведенные расчеты показали, что в зависимости от того, какие критерии простые или дисконтированные выбраны за основу при выборе проекта, могут быть сделаны диаметрально противоположные выводы.
3. Критерии, основанные на дисконтированных оценках для независимых единичных проектов с ординарными денежными потоками, дают одинаковые рекомендации по поводу принятия или игнорирования проекта.
4. Учитывая взаимосвязи параметров инвестиционного проекта, возможна его модернизация и улучшение показателей эффективности.
5. При неординарных денежных потоках инвестиционного проекта возникает множественность значений ВНД, которая устраняется введением в рассмотрение модифицированной внутренней нормы доходности (МВНД).
Учет инфляции и риска
Инфляция − процесс обесценивания денег и приводящий как следствие к росту цен, заметно влияет на эффективность инвестиционного проекта. Иногда выгодный при отсутствии инфляции проект может оказаться убыточным при её учете. Существует два принципиальных подхода для учета инфляции в инвестиционных проектах. Более корректной, но трудоёмкой является методика корректировки всех факторов влияющих на денежные потоки проектов (выручка, затраты, в том числе переменные и постоянные, материальные и трудовые ресурсы, амортиза
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.018 с.) |

 =
=  = 12,3 года.
= 12,3 года.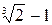 = 0,26 или 26 % годовых.
= 0,26 или 26 % годовых. )(1+
)(1+  )(1+
)(1+  )=1∙1,6∙1,35∙1,4∙1,45=4,385
)=1∙1,6∙1,35∙1,4∙1,45=4,385 3.Табулированный коэффициент F6(i, n) = 1/F4(i, n) = i / [1− (1+i)– n] показывает, какую одинаковую величину необходимо периодически вносить n лет под i %, для погашения одной денежной единицы (взнос на амортизацию долга).
3.Табулированный коэффициент F6(i, n) = 1/F4(i, n) = i / [1− (1+i)– n] показывает, какую одинаковую величину необходимо периодически вносить n лет под i %, для погашения одной денежной единицы (взнос на амортизацию долга). = R − const, известны процентная ставка i и горизонт расчета проекта Т.
= R − const, известны процентная ставка i и горизонт расчета проекта Т.


