
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка точности функции измеренных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
На содержание этого раздела следует обратить особое внимание и учесть порядок определения СКП функции, вычисляемой по измеренным величинам (аргументам) с СКП, связанными с искомой величиной функционально. Функция задана в общем виде:
где СКП функции
где Порядок вычисления СКП функции общего вида следующий: 1) составляем функцию, связывающую оцениваемую величину с измеренными величинами, например (объем цилиндра):
где
Объем цилиндра является функцией двух аргументов – радиуса и высоты, а 2) применяя формулу (3.6), записываем СКП V в общем виде:
3) находим частные производные:
4) полученные выражения частных производных подставляем в формулу СКП функции:
5) в соответствии с условием задачи в полученную формулу подставляем числовые значения аргументов и их СКП и вычисляем величину
Решение задач Пример 3. Пусть проложен висячий теодолитный ход. Горизонтальные углы хода Решение. Для определения погрешности дирекционного угла последней линии,прежде всего, необходимо представить этот дирекционный угол как функцию исходных и измеренных величин. Так как были измерены правые по ходу углы, искомый дирекционный угол может быть вычислен по формуле
На основании формулы (3.6) для СКП дирекционного угла последней линии хода можно записать
Получим
или
Окончательно можно сделать вывод, что при передаче дирекционных углов случайные погрешности накапливаются пропорционально корню квадратному из числа измеренных горизонтальных углов. Пример 4. Для получения горизонтального проложения линии на плане определены координаты концов этой линии, что дало результаты Решение Горизонтальное проложение между точками определяют по формуле:
Применим формулу (3.6) и вычислим частные производные
Аналогично:
Тогда СКП горизонтального проложения определяется формулой
При условии, что
или
Пример 5. Для получения дирекционного угла направления между точками на плане определены координаты концов отрезка, соединяющие эти точки ( Решение. Дирекционный угол направления вычисляют по формуле:
где Согласно (3.6) необходимо вычислить частные производные
Окончательно:
Аналогично найдем частные производные
СКП дирекционного угла определяется формулой
где При условии, что
Пример 6. Вычислить приращения координат и их СКП по линии длиной 250,17 м, имеющей дирекционный угол 63°27,0', если Решение. Известно, что приращения координат
Найдем
Тогда
При вычислениях величина
Подставив соответствующие значения величин, получаем
Окончательно
Задача 3. Найти СКП превышения, полученного из геометрического нивелирования методом из середины по черным сторонам реек, принимая СКП отсчета по рейке Задача 4. Линия теодолитного хода Задача 5. Определить СКП превышения, вычисленного на станции геометрического нивелирования методом из середины по черным и красным сторонам реек, если СКП отсчета по рейке Задача 6. Вычислить превышение, полученное тригонометрическим нивелированием, и его предельную погрешность, если расстояние, измеренное нитяным дальномером D =210,5 м с СКП Задача 7. При определении расстояния АВ, недоступного для измерения лентой, в треугольнике AВС были измерены: базис AС =84,55 м с СКП базиса Вычислить расстояние АВ и ее СКП. Задача 9. В треугольнике измерены основание Задача 10. В треугольнике измерены две стороны
|
||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 531; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.009 с.) |

 , (3.5)
, (3.5) – аргументы, полученные из измерений с СКП
– аргументы, полученные из измерений с СКП  .
. вычисляется по формуле:
вычисляется по формуле: , (3.6)
, (3.6)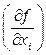 – частные производные функции по каждому аргументу.
– частные производные функции по каждому аргументу. ,
,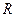 – радиус основания цилиндра;
– радиус основания цилиндра; – высота цилиндра.
– высота цилиндра. – постоянная;
– постоянная; ;
; ,
,  ;
; ;
;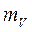 .
. измерялись независимо друг от друга в одинаковых условиях с СКП
измерялись независимо друг от друга в одинаковых условиях с СКП  . Найти СКП
. Найти СКП  дирекционного угла последней линии рассматриваемого хода. При этом будем считать
дирекционного угла последней линии рассматриваемого хода. При этом будем считать  величиной безошибочной.
величиной безошибочной.
 .
. ,
,
 ,
,  и
и  ,
,  . Эти величины получены со СКП
. Эти величины получены со СКП  и
и  ,
,  и
и  . Необходимо вычислить горизонтальное проложение между этими точками и его СКП.
. Необходимо вычислить горизонтальное проложение между этими точками и его СКП.
 по всем координатам:
по всем координатам: .
.

 .
. .
. , будем иметь:
, будем иметь: ,
,
 ,
,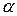 по всем координатам:
по всем координатам: .
.
 .
. 
 .
.
 .
.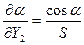 .
. ,
, - радианная мера угла в секундах, равная 206265".
- радианная мера угла в секундах, равная 206265". , будем иметь:
, будем иметь: .
. и
и  ,0'.
,0'. ,
,  рассчитывают по формулам
рассчитывают по формулам  и
и  , что дает результаты
, что дает результаты  и
и  . СКП приращений координат могут быть получены из соотношений
. СКП приращений координат могут быть получены из соотношений ,
, .
. :
:
 ;
; .
. должна быть представлена в радианной мере, но в условии задачи она задается в градусной мере. С учетом этого предыдущие формулы примут вид
должна быть представлена в радианной мере, но в условии задачи она задается в градусной мере. С учетом этого предыдущие формулы примут вид ;
; .
.

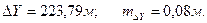
 равной 1 мм.
равной 1 мм.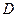 измерена частями с СКП
измерена частями с СКП  м,
м,  м,
м,  м. Определить СКП
м. Определить СКП  длины линии
длины линии  м; угол наклона визирной оси при визировании на верх рейки ν = ……(см. приложение табл. 2) с СКП
м; угол наклона визирной оси при визировании на верх рейки ν = ……(см. приложение табл. 2) с СКП 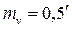 ; высота прибора i = 1,30 м с СКП
; высота прибора i = 1,30 м с СКП  м; длина рейки V = 3,00 м с СКП
м; длина рейки V = 3,00 м с СКП  м.
м. м; углы A=56°27,0' и С=35°14,0' со СКП, равной
м; углы A=56°27,0' и С=35°14,0' со СКП, равной  =0,5'.
=0,5'.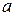 и высота
и высота 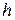 с погрешностями, соответственно равными
с погрешностями, соответственно равными  и
и  . Найти СКП площади треугольника.
. Найти СКП площади треугольника. и
и  и угол
и угол  между ними с СКП, соответственно равными
между ними с СКП, соответственно равными  и
и  . Найти СКП площади треугольника.
. Найти СКП площади треугольника.


