
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение с теорией. Функциональные шкалыСодержание книги Поиск на нашем сайте
Для проверки теоретической зависимости на график наносят опытные точки (нередко с указанием их погрешности), а теоретическую кривую проводят через точки, рассчитанные по уравнению. Если теория дает лишь вид зависимости, а параметры ее неизвестны и их надлежит определить из опыта, то экспериментальную зависимость стараются привести к линейному виду (т.к. параметры прямой найти нетрудно). С этой целью при построении графика по осям откладывают не сами измеренные величины, а такие функции этих величин, которые позволяют сделать зависимость линейной. Например, в лабораторной работе №10 «Изучение зависимости электрической проводимости и сопротивления полупроводников от температуры» линейной функцией будет являться зависимость натурального логарифма удельной электрической проводимости от обратной температуры Определение параметров линейной зависимости
Рассмотрим приближенный метод определения параметров линейной зависимости. Приближенный метод.
Параметр b линейной зависимости находят по графику как ординату точки пересечения прямой с осью Y. Величину b можно найти и по уравнению прямой, подставляя координата средней точки графика:
Случайные погрешности параметров определяются разбросом опытных точек относительно проведенной прямой. Для простейшей оценки этих погрешностей достаточно найти на графике величину Dy – отклонение от прямой линии наиболее удаленной точки, и (yN – y1) – интервал, на котором сделаны измерения (длина оси у). Абсолютная случайная погрешность параметра b равна:
Для углового коэффициента прямой К сначала вычисляют относительную погрешность
Эта формула удобна тем, что при расчете отношения (4) можно подставлять величины в любых единицах (всего удобнее – в миллиметрах шкалы по оси у). Затем находят абсолютную погрешность величины K:
которая позволяет записать значение углового коэффициента К с указанием абсолютной погрешности
Доверительная вероятность P[6] в описанном методе оценки погрешностей (по максимальному отклонению Dy) зависит от числа опытных точек N: чем больше N, тем выше надежность результата:
ПРИЛОЖЕНИЕ 2 (обложка лабораторной тетради) МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Факультет арктических технологий
Кафедра общей и прикладной физики тетрадь для выполнения лабораторных работ по курсу физики по разделу «Электричество. Магнетизм. Колебательные процессы» студента 1 курса ФАТ, гр. Эл141(1) ____________________ (ф.и.о.)
Мурманск-2016
ЛАБОРАТОРНАЯ РАБОТА № 3 ( в редакции Власовой С.В.- 2015) ГРАДУИРОВКА ГАЛЬВАНОМЕТРА И РАЗЛИЧНЫЕ СХЕМЫ ЕГО ВКЛЮЧЕНИЯ Цель работы: ознакомиться с методами расширения диапазона измерений электроизмерительных приборов. Приборы и принадлежности: гальванометр магнитоэлектрической системы, реостат, сопротивления, магазин сопротивлений.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Гальванометры – высокочувствительные приборы, предназначенные для измерения малых токов, напряжений и количеств электричества. В них используется облегчённый измерительный механизм, в котором рамка подвешена на тонкой упругой нити. Используя гальванометр для измерений в электрических цепях, необходимо знать его основные параметры.
1. Ток полного отклонения I r, вызывающий отклонение стрелки на всю шкалу; пропускать через гальванометр ток, больший I r, нельзя. 2. Внутреннее сопротивление гальванометра R r, которое обусловлено сопротивлением проводов, рамки, контактов и т.п. 3. Напряжение полного отклонения U r. Именно при этом напряжении, поданном на зажимы (клеммы) прибора, через него протекает ток I r, отклоняющий стрелку на всю шкалу. Все три вышеназванные величины связаны между собой законом Ома для однородного участка цепи:
На практике гальванометр приходиться использовать для измерения токов и напряжений, превышающих его паспортные значения I r и U r. Очевидно, что включение гальванометра непосредственно в цепь, через которую протекает, например, ток I > I r, приведёт к выходу гальванометра из строя. Для расширения пределов измерений гальванометра используются специальные методы. Предположим, что с помощью гальванометра с заданными значениями R r и I r нужно измерить ток I, больший I r. В этом случае гальванометр преобразуется в амперметр, состоящий из собственно гальванометра и низкоомного сопротивления (шунта), включённого параллельно гальванометру (рис. 3.1). Роль шунта заключается в том, что за счёт его малого сопротивления через него протекает значительная часть измеряемого тока, а через гальванометр при этом протекает ток, не превышающий значение I r.
Рис. 3.1. Использование гальванометра в качестве амперметра.
Сопротивление шунта можно рассчитать, используя правила Кирхгофа для разветвлённых цепей. Выберем направления токов I, I r, и I ш так, как показано на рис. 3-1 (направление токов задаётся произвольно). Воспользуемся первым правилом Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю. (Напоминаем, что ток, входящий в узел, считается положительным, а выходящий – отрицательным). Запишем первый закон Кирхгофа для любого из узлов цепи:
I – I r – I ш = 0. (1)
Второе правило Кирхгофа утверждает: для произвольного замкнутого контура, выделенного в разветвлённой цепи, алгебраическая сумма произведений сил токов на сопротивление соответствующих участков контура, равна алгебраической сумме э.д.с., действующих в контуре. Воспользуемся вторым правилом Кирхгофа для замкнутого контура, составленного из гальванометра и шунта (выберем направление обхода «по часовой стрелке»): I r × R r – I ш × R ш = 0 (2) Решая совместно уравнения (1) и (2), найдем сопротивление шунта:
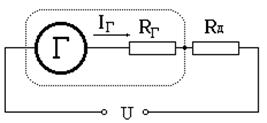
где Гальванометр также можно использовать для измерения напряжения U, причем и в случае, если U > U Г. Для этого необходимо последовательно с гальванометром включить добавочное сопротивление R доб (рис.3.2). Из школьного курса физики Вы знаете, что при последовательном соединении элементов в цепь напряжение на участке цепи равно сумме падений напряжений на каждом из элементов этого участка:
Рис. 3.2. Использование гальванометра в качестве вольтметра.
Учитывая, что при последовательном соединении через гальванометр и добавочное сопротивление протекает один и тот же ток I r, можно записать:
откуда следует, что:
Следует понимать, что в результате включения в цепь Rш и Rдоб цена деления (и чувствительность) полученного амперметра (или вольтметра) не будет равна цене деления (или чувствительности) гальванометра. По указанной причине необходимо провести градуировку прибора уже в качестве амперметра или вольтметра, т.е. сопоставить делениям шкалы гальванометра значения тока или напряжения, полученные в результате измерений.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.14.251 (0.01 с.) |

 .
. Пусть измеренные величины х и у связаны линейной зависимостью вида у=Кх+b и нужно определить ее параметры К и b. Для этого опытные точки наносят на график и проводят прямую линию, руководствуясь правилами построения графика. На концах линии выбирают две произвольные точки а и б, удобные для расчета. Для простоты расчета и снижения погрешности отсчета по графику удобно точку а взять на одной из осей, а точку б - так, чтобы при расчете К отрезок (хб-ха) позволял обойтись без микрокалькулятора. Среднее значение углового коэффициента К вычисляют как отношение, определяющее наклон прямой:
Пусть измеренные величины х и у связаны линейной зависимостью вида у=Кх+b и нужно определить ее параметры К и b. Для этого опытные точки наносят на график и проводят прямую линию, руководствуясь правилами построения графика. На концах линии выбирают две произвольные точки а и б, удобные для расчета. Для простоты расчета и снижения погрешности отсчета по графику удобно точку а взять на одной из осей, а точку б - так, чтобы при расчете К отрезок (хб-ха) позволял обойтись без микрокалькулятора. Среднее значение углового коэффициента К вычисляют как отношение, определяющее наклон прямой: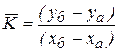 . (1)
. (1) (2)
(2) (3)
(3) . (4)
. (4) (5)
(5)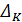 :
: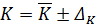 (6)
(6) . (7)
. (7) .
.
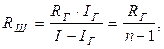 (3)
(3) .
. .
.

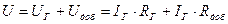 , (4)
, (4) (5)
(5)


