
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция нескольких переменныхСодержание книги
Поиск на нашем сайте
Рассмотрим случай, когда
Ошибки в величинах
где
где коэффициенты
Эти частные производные вычисляются в точках
Усредним обе части этого равенства по парам значений По определению,
Следовательно,
Таблица 32.1. Операции над ошибками
Теперь можно установить общее правило. Пусть
где
и т.д. Выражение для
Ошибки и методика эксперимента
Если интересующая нас величина Таким образом, величины Другое дело, когда Случай 1
В данном случае большая величина Теперь рассмотрим Случай 2
Обе непосредственно измеряемые величины определены с точностью 2 %, а точность конечной величины оказывается равной 75 %. Таким образом, вычисляя разность двух близких независимо измеренных величин, мы сталкиваемся с принципиальной неприятностью: окончательная ошибка сильно возрастает. Значит, нужно по возможности найти иной метод измерения В дальнейших лекциях мы приведем примеры экспериментальных методов, которые позволяют использовать преимущества случая 1 и избегать случая 2. Эти примеры показывают, как учет ошибок измерения оказывает влияние непосредственно на методику эксперимента. А теперь рассмотрим один гипотетический пример. Допустим, что требуется определить величину
Следовательно, Предположим, что у нас есть еще резерв времени, который позволяет снизить ошибку измерения одной из величин, скажем, вдвое. Какой из них отдать предпочтение? Если это время затратить на измерение величины Мораль такова: основное внимание нужно всегда уделять тем величинам, которые дают наибольший вклад в окончательную ошибку. Вообще говоря, необходимо так планировать эксперимент, чтобы ни одна из величин не вносила в конечный результат ошибки, значительно превышающей ошибки остальных величин. В приведенном примере очевидно, что измерения, в которых
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.49.19 (0.006 с.) |

 - функция двух переменных
- функция двух переменных  и
и  :
: . (32.9)
. (32.9) , (32.10)
, (32.10) , (32.11)
, (32.11) и
и 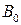 - истинные значения величин
- истинные значения величин  , (32.12)
, (32.12) и
и  даются выражениями
даются выражениями , (32.13)
, (32.13) . (32.14)
. (32.14) и
и 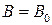 . Из последнего равенства следует, что
. Из последнего равенства следует, что . (32.15)
. (32.15) равно нулю.
равно нулю.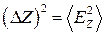 , (32.16)
, (32.16) , (32.17)
, (32.17) . (32.18)
. (32.18) . (32.19)
. (32.19)


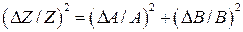



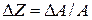


 и т.д. Пусть среднеквадратичная ошибка в величине
и т.д. Пусть среднеквадратичная ошибка в величине  и т. д. Тогда среднеквадратичная ошибка
и т. д. Тогда среднеквадратичная ошибка  в величине
в величине  , (32.20)
, (32.20) (32.21)
(32.21) или
или  , то ошибка на х % в величине
, то ошибка на х % в величине  или
или  . Здесь все зависит от того, сильно ли разнятся величины
. Здесь все зависит от того, сильно ли разнятся величины 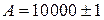




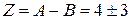

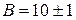
 %,
%,  = 10 %, а
= 10 %, а  %.
%. = 1 %, что приведет к
= 1 %, что приведет к  %. Если же уточнить
%. Если же уточнить  %. Итак, в первом случае окончательная ошибка мало изменилась, а во втором она уменьшилась почти вдвое.
%. Итак, в первом случае окончательная ошибка мало изменилась, а во втором она уменьшилась почти вдвое.


