
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение случайной и приборной погрешностей. Полная погрешность измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть результаты наблюдений наряду со случайной содержат и систематическую приборную погрешность
Однако ее наличие совершенно не влияет на случайную погрешность результата измерения. Смещение среднего и доверительного интервала может привести к тому, что истинное значение Чтобы этого не произошло, необходимо расширить доверительный интервал на величину верхней границы возможных значений погрешностей прибора
где
Рис. 31.6. К определению полной погрешности измерения
Указанный способ суммирования погрешностей дает максимальную верхнюю границу полной погрешности результата измерения. Однако маловероятно, что в данном эксперименте полная погрешность примет своё максимальное значение. Учитывая, что, как правило, на практике приборная погрешность, как отдельного прибора (погрешности квантования и шкалы прибора), так и в серии приборов изменяется нерегулярным образом, оставаясь в границах
Сопоставляя это выражение с неравенством треугольника
можно заключить, что в качестве разумной оценки полной погрешности результата измерения можно выбрать величину
Строгое рассмотрение суммирования случайной и приборной погрешностей основано на построении совместной функции плотности распределения вероятности
Можно построить доверительный интервал для совместной функции распределения случайной и приборной погрешностей. Полученное выражение для полной погрешности результата измерения хорошо (с точностью до 5%) аппроксимируется формулой. Итоговая запись результата измерения будет иметь вид
с вероятностью
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.240.14 (0.008 с.) |

 , которую можно считать постоянной в течение времени проведения измерения, так как характеристики прибора за это время не успевают заметно измениться. Наблюдаемые в опыте результаты наблюдений будут при этом равны
, которую можно считать постоянной в течение времени проведения измерения, так как характеристики прибора за это время не успевают заметно измениться. Наблюдаемые в опыте результаты наблюдений будут при этом равны  . Наличие постоянной погрешности, вносимой прибором в результаты наблюдений, приводит к смещению выборочного среднего
. Наличие постоянной погрешности, вносимой прибором в результаты наблюдений, приводит к смещению выборочного среднего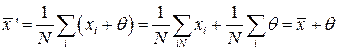 . (31.34)
. (31.34) измеряемой величины окажется за пределами найденного доверительною интервала
измеряемой величины окажется за пределами найденного доверительною интервала 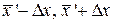 , как это показано на рис. 31.6.
, как это показано на рис. 31.6. и результат измерения можно записать в виде
и результат измерения можно записать в виде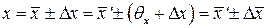 , (31.35)
, (31.35) назовём полной погрешностью результата измерения. Новый доверительный интервал (
назовём полной погрешностью результата измерения. Новый доверительный интервал (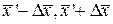 ) обязательно накроет истинное значение
) обязательно накроет истинное значение  (рис. 31.6). Отметим, что доверительная вероятность, соответствующая найденному таким образом доверительному интервалу, будет превышать доверительную вероятность, используемую для нахождения случайной составляющей погрешности измерения.
(рис. 31.6). Отметим, что доверительная вероятность, соответствующая найденному таким образом доверительному интервалу, будет превышать доверительную вероятность, используемую для нахождения случайной составляющей погрешности измерения.
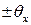 , полная погрешность результата измерения с учетом неизвестности величины и знака
, полная погрешность результата измерения с учетом неизвестности величины и знака  . (31.36)
. (31.36)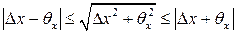 (31.37)
(31.37)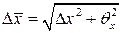 (31.38)
(31.38)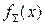 . Будем считать, что в интервале (
. Будем считать, что в интервале ( ) все возможные значения приборной погрешности равновероятны, то есть приборная погрешность распределена равномерно. Тогда совместная функция распределения
) все возможные значения приборной погрешности равновероятны, то есть приборная погрешность распределена равномерно. Тогда совместная функция распределения  (или распределения Стьюдента для конечного числа наблюдений
(или распределения Стьюдента для конечного числа наблюдений  ) и равномерного
) и равномерного 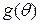 законов распределения:
законов распределения: . (31.39)
. (31.39)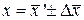 (31.40)
(31.40)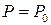 , где
, где  - вероятность определения случайной составляющей погрешности измерения.
- вероятность определения случайной составляющей погрешности измерения.


