
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запись и округление результата измеренияСодержание книги
Поиск на нашем сайте
Погрешность результата рассчитывается по случайной выборке, и сама содержит погрешность. Новое измерение (новая выборка) даст новую погрешность, отличную от первой. Можно считать, что объективную информацию о величине погрешности несут лишь одна - две значащие цифры в её численном выражении. Остальные значащие цифры можно считать случайными. Результат измерения также содержит лишь ограниченное число значащих цифр, несущих информацию о величине этого результата. В связи с этим численные значения результата и погрешности должны быть округлены. При округлении используют следующие правила: 1. Предварительно результат и погрешность записывают в нормальном виде: общий показатель степени выносят за скобку или заменяют соответствующей приставкой: микро, милли, кило, мега и др. Например,
Запрещены записи вида 2. Если результат будет в дальнейшем использован в вычислениях, то во избежание накопления погрешностей за счет округлений погрешность округляют до двух значащих цифр при любой первой. При промежуточных вычислениях величин 3. Если результат измерения является окончательным и не будет использован в вычислениях других величин, то доверительную погрешность 4. Среднее значение
Ошибки косвенных измерений
В большинстве экспериментов интересующая нас величина непосредственно не измеряется. Вместо этого мы измеряем некоторые другие величины Например, измерить плотность
Допустим, что каждая величина измеряется несколько раз. В таком случае, для величины Зная величины
Рис. 32.1. Ошибка
Функция одной переменной
Рассмотрим сначала случай, когда
(Здесь Если истинное значение первичной величины есть
Ошибка данного значения
и ей соответствует ошибка в величине
Производная Таким образом, ошибка в величине
Теперь допустим, что величина
Отметим один важный случай, когда
т.е. относительная среднеквадратичная ошибка в величине
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.116.77 (0.006 с.) |

 . (31.41)
. (31.41)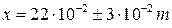 или
или 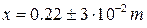 . Показатель 101 не выносится.
. Показатель 101 не выносится. и
и 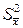 (из которых впоследствии будет извлекаться квадратный корень для нахождения
(из которых впоследствии будет извлекаться квадратный корень для нахождения  и
и 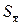 ) следует сохранять не менее четырех значащих цифр.
) следует сохранять не менее четырех значащих цифр.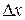 округляют до первой значащей цифры, если она равна или больше 2, или до двух значащих цифр, если первая равна 1.
округляют до первой значащей цифры, если она равна или больше 2, или до двух значащих цифр, если первая равна 1. округляют до того разряда, которым оканчивается округленная погрешность
округляют до того разряда, которым оканчивается округленная погрешность  0.10.
0.10.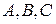 и т.д., а затем вычисляем величину
и т.д., а затем вычисляем величину  , которая является известной функцией первичных величин.
, которая является известной функцией первичных величин. некоторого материала можно, измеряя массу прямоугольного бруска
некоторого материала можно, измеряя массу прямоугольного бруска 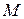 и его размеры
и его размеры 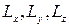 . Функциональная связь между искомой величиной и первичными величинами имеет вид:
. Функциональная связь между искомой величиной и первичными величинами имеет вид: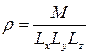 . (32.1)
. (32.1) мы найдем наилучшее значение
мы найдем наилучшее значение 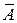 , т.е. среднее из измеренных значений, и оценку его среднеквадратической ошибки
, т.е. среднее из измеренных значений, и оценку его среднеквадратической ошибки  . Аналогичным образом найдем
. Аналогичным образом найдем  и
и 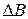 и т.д. Предположим, что измерения первичных величин независимы и поэтому их ошибки также независимы.
и т.д. Предположим, что измерения первичных величин независимы и поэтому их ошибки также независимы. величины
величины 
 в величине
в величине  в величине
в величине 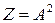 или
или  . В общем случае запишем это так:
. В общем случае запишем это так: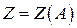 (32.2)
(32.2) , то истинное значение величины
, то истинное значение величины 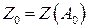 . (32.3)
. (32.3) (32.4)
(32.4)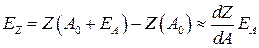 . (32.5)
. (32.5)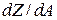 взята в точке
взята в точке  можно представить прямой линией.
можно представить прямой линией.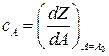 . (32.6)
. (32.6) . (32.7)
. (32.7) , так что
, так что  . В этом случае
. В этом случае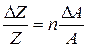 , (32.8)
, (32.8) раз больше относительной среднеквадратичной ошибки в величине
раз больше относительной среднеквадратичной ошибки в величине 


