
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ результатов совместных измеренийСодержание книги
Поиск на нашем сайте
33.1. Цель и особенности эксперимента по определению функциональной зависимости
На практике сама необходимость измерений большинства величин вызывается именно тем, что они не остаются постоянными, а изменяются в функции от изменения других величин. В этом случае целью измерений является установление вида функциональной зависимости Определение математической модели включает в себя указание вида модели и определение значений ее параметров (коэффициентов, показателей степени и т. д.). Искомая функция может быть как функцией одной независимой переменной, так и функцией многих переменных. В современной теории эксперимента независимые переменные принято называть факторами, а зависимую переменную y - откликом. В соответствием с этим эксперимент по определению функции вида y=f (x) принято именовать однофакторным, а эксперимент по определению функции вида y = f (x 1, x 2,..., x k) - многофакторным. Именно однофакторный эксперимент мы и будем подробно рассматривать. Однако большинство методов обработки прямо переносятся и в случае многофакторного эксперимента. Возможны два основных варианта реализации совместных измерений величин x и y: активный и пассивный эксперимент. В активном (или планируемом) эксперименте значения аргумента x 1, x 2,..., x k выбирают заранее и последовательно воспроизводят эти значения, выполняя при каждом фиксированном значении аргумента x i измерение соответствующей величины y i. В этом случае x называют контролируемой переменной. В пассивном (непланируемом) эксперименте значения аргумента заранее не выбирают, а измеряют те значения x i, которые заданы каким-либо образом или произвольно выбраны из числа возможных. При тех же значениях x i измеряют также соответствующие величины y i. Во многих случаях активный эксперимент является предпочтительным, поскольку за счет рационального выбора значений x i можно получить более точные оценки зависимости, а для обработки можно применять более широкий класс оценок. Однако на практике это не всегда можно реализовать. Искомая математическая модель функциональной зависимости
Рис. 33.1.. Результаты однофакторного эксперимента
Разделить погрешности, вызванные неточностью измерений x и неточностью измерений y, невозможно, так как смещение точки, например выше кривой, могло быть вызвано как положительной погрешностью при измерении y, так и отрицательной погрешностью при измерении x. Поэтому описанием погрешности исходных данных может быть лишь указание ширины полосы их разброса вокруг найденной кривой зависимости Искомая зависимость Способ задания зависимости определяет обработку данных при ее построении. Если зависимость задается таблицей Если зависимость задается аналитически, то в дополнение к этому необходима обработка всего набора данных в целом. При этом задается определенный функциональный вид зависимости и вычисляют оценки ее параметров. Для графического способа задания зависимости возможны два варианта, близкие к одному из упомянутых выше случаев. Если график строится поточечно (без сглаживания), то выполняется лишь обработка данных в каждой из точек. В промежутках между ними зависимость определяется, например, путем интерполяции. Если график строится со сглаживанием, ориентируясь на определенный функциональный вид зависимости, то обработка выполняется, как и при аналитическом представлении.
33.2. Некоторые определения
Когда вы имеете дело с выборкой экспериментальных данных, то они, чаще всего, представляются в виде массива, состоящего из пар чисел 1. 2. должна некоторым образом (например, в виде определенной аналитической зависимости) приближать 3. должна приближать экспериментальную зависимость
Рис. 33.2. Различные типы аппроксимации экспериментальных данных
Различные виды построения аппроксимирующей зависимости
Интерполяция
Пусть задан дискретный набор точек В качестве функции
Глобальная интерполяция
При глобальной интерполяции ищется единый полином для всего интервала. Если среди узлов Запишем систему уравнений для определения коэффициентов полинома:
Определим матрицу коэффициентов системы уравнений А:
и вектор-столбец свободных членов b
Система линейных алгебраических уравнений относительно неизвестных будет иметь решение, если определитель системы (определитель матрицы А) отличен от нуля. Определитель матрицы А, известный в алгебре как определитель Вандермонда, имеет аналитическое выражение
Из этого выражения видно, что Решение системы уравнений представляет собой самостоятельную и достаточно трудоемкую задачу. Но использование математических пакетов, в частности - MathCAD, позволяет решать ее удивительно легко и изящно. Достаточно просто записать решение в матричном виде (рис. 33.3). С увеличением количества узлов возрастает и степень интерполяционного полинома, что приводит к резкому увеличению погрешности в результате возникновения так называемого явления волнистости. Кроме того, для целого ряда функций глобальная интерполяция полиномом вообще не дает удовлетворительного результата.
Рис. 33.3. Решение задачи интерполяции полиномом в MathCAD
Для того чтобы избежать высокой степени полинома отрезок интерполяции разбивают на несколько частей и на каждом частичном интервале строят самостоятельный полином невысокой степени. Далее мы рассмотрим наиболее часто используемые виды интервальной интерполяции, а также способы их реализации в MathCAD
Локальная интерполяция
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.239.25 (0.006 с.) |

 . Для этого должны одновременно определятся как значения x, так и соответствующие им значения y, а задачей эксперимента является, как принято теперь говорить, установление математической модели исследуемой зависимости.
. Для этого должны одновременно определятся как значения x, так и соответствующие им значения y, а задачей эксперимента является, как принято теперь говорить, установление математической модели исследуемой зависимости. может быть найдена лишь в результате совместной обработки всех полученных значений x и y. На рис. 33.1 это кривая, проходящая по центру полосы экспериментальных точек, которые могут и не лежать на искомой кривой
может быть найдена лишь в результате совместной обработки всех полученных значений x и y. На рис. 33.1 это кривая, проходящая по центру полосы экспериментальных точек, которые могут и не лежать на искомой кривой 
 , может быть представлена в различном виде: аналитически (формулой), графически или в виде таблицы. Выбор способа представления зависит от функционального вида и сложности зависимости, а также от способа ее дальнейшего использования на практике. Обычно предпочитают задавать ее в аналитическом виде формулой, поскольку такая форма представления наиболее компактна и позволяет решать широкий круг практических задач. Однако в тех случаях, когда зависимость нельзя достаточно точно аппроксимировать простой функцией или аналитическое построение оказывается слишком трудоемким, приходится задавать ее с помощью графика или таблицы.
, может быть представлена в различном виде: аналитически (формулой), графически или в виде таблицы. Выбор способа представления зависит от функционального вида и сложности зависимости, а также от способа ее дальнейшего использования на практике. Обычно предпочитают задавать ее в аналитическом виде формулой, поскольку такая форма представления наиболее компактна и позволяет решать широкий круг практических задач. Однако в тех случаях, когда зависимость нельзя достаточно точно аппроксимировать простой функцией или аналитическое построение оказывается слишком трудоемким, приходится задавать ее с помощью графика или таблицы. ,
,  в каждой точке порознь согласно обычным правилам обработки данных при прямых или косвенных измерениях.
в каждой точке порознь согласно обычным правилам обработки данных при прямых или косвенных измерениях.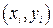 . Поэтому возникает задача аппроксимации дискретной зависимости
. Поэтому возникает задача аппроксимации дискретной зависимости  непрерывной функцией
непрерывной функцией  . Функция
. Функция  . В этом случае говорят об интерполяции данных функцией
. В этом случае говорят об интерполяции данных функцией  , или экстраполяции за пределами интервала, содержащего все
, или экстраполяции за пределами интервала, содержащего все 
 , называемых узлами интерполяции, причем среди этих точек нет совпадающих, а так же значения функции
, называемых узлами интерполяции, причем среди этих точек нет совпадающих, а так же значения функции  . Такой способ введения функции называют лагранжевой интерполяцией, а условия - условиями Лагранжа.
. Такой способ введения функции называют лагранжевой интерполяцией, а условия - условиями Лагранжа. .
. (33.1)
(33.1) (33.2)
(33.2) (33.3)
(33.3) (33.4)
(33.4)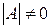 , если среди узлов
, если среди узлов 



