
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное или гауссово распределениеСодержание книги
Поиск на нашем сайте
Одним из часто встречающихся на практике распределений является нормальный или гауссовский закон. Ему подчиняются физические величины, случайность которых обусловлена действием множества независимых (или слабо зависимых) малых аддитивных факторов, результат воздействия каждого из которых мал по сравнению с их суммарным воздействием. Плотность распределения вероятности нормального закона имеет вид
где Поскольку гауссово распределение симметрично относительно
Вводя
Рис. 31.5. Нормальное распределение
где Можно показать, что если значения Если средние значения
Откуда для границ доверительного интервала
где Это неравенство принято записывать в виде символического равенства
где
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.005 с.) |

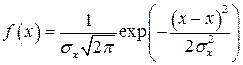 , (31.7)
, (31.7) - случайное значение величины. Параметр
- случайное значение величины. Параметр  определяет центр распределения, а
определяет центр распределения, а  форму и ширину кривой плотности распределения, что показано на рис. 31.5. Множитель
форму и ширину кривой плотности распределения, что показано на рис. 31.5. Множитель  перед экспонентой, определяющий высоту гауссовской кривой, выбран таким образом, чтобы было выполнено условие нормировки.
перед экспонентой, определяющий высоту гауссовской кривой, выбран таким образом, чтобы было выполнено условие нормировки. ), будет равна
), будет равна . (31.8)
. (31.8) , называемую стандартизованной переменной, можно записать
, называемую стандартизованной переменной, можно записать , (31.9)
, (31.9)
 - коэффициенты, определяющие ширину интервала в единицах параметра нормального распределения
- коэффициенты, определяющие ширину интервала в единицах параметра нормального распределения  . Вероятности
. Вероятности  попадания
попадания  в интервал (
в интервал ( ) можно найти, вычислив интеграл численно для различных значений ширины интервала
) можно найти, вычислив интеграл численно для различных значений ширины интервала  получим
получим  с вероятностью
с вероятностью  также распределены по нормальному закону с центром в точке
также распределены по нормальному закону с центром в точке  , где
, где  - объем выборок, по которым рассчитываются
- объем выборок, по которым рассчитываются  .
. и переходу к доверительному интервалу переменной
и переходу к доверительному интервалу переменной  . (31.10)
. (31.10) , (31.11)
, (31.11) , (31.12)
, (31.12) - случайная доверительная погрешность результата измерения.
- случайная доверительная погрешность результата измерения.


